Сфера – множина (геометричне місце) точок простору, рівновіддалених від фіксованої точки. Ця фіксована точка O(x0; y0; z0) називається центром сфери, а відстань від довільної точки сфери до її центра називається радіусом сфери R.
Канонічне рівняння сфери:
x2+y2+z2=R2, де R - радіус сфери.
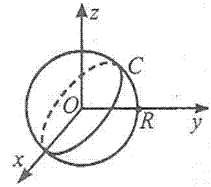
Формула сфери з центром у точці O(x0; y0; z0) і радіусом R:
(x-x0)2+(y-y0)2+(z-z0)2=R2
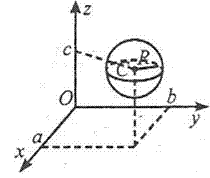
Будь-яка дотична пряма або площина перпендикулярна до радіуса сфери в точці дотику.
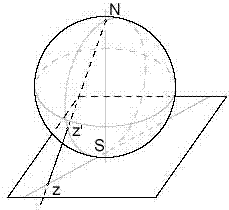
Основні формули сфери
- Площа сфери
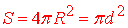
- Об'єм кулі, обмеженої сферою
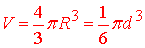
- Площа сегменту сфери
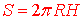
Сегмент сфери- смуга між екватором і широтою, проведеною на висоті H над екватором.
Чимало задач на площу поверхні сфери і об'єм кулі Ви розглянули в шкільному курсі, проте це не складні задачі. Тут же будуть проаналізовані приклади, які Вас чекають при навчанні у ВУЗах. Уважно вивчайте їх та використовуйте на практиці.
Задачі на складання рівнянь сфери
Задача 6.1.1 Запишіть рівняння сфери, яка:
- має центр в точці (2;-1;3) і радіус R=6;
- має центр в початку координат (0;0;0) і проходить через точку (6;-2;3);
- має центр в точці (1;4;-7) і дотикається до площини 6x+6y-7z+42=0;
- має центр в точці (6;-8;3) і дотикається до осі аплікат.
Розв'язання: Наведена схема обчислень універсальна і застосовується в ряді подібних завдань.
1) Маємо координати центра O(x0;y0;z0) і радіус сфери R.
Складемо рівняння сфери з центром у точці (2;-1;3) і радіусом R=6:
(x-2)2+(y+1)2+(z-3)2=36.
Це найбільш простий приклад з яким може справитися і школяр.
2) Задано координати центра сфери O(x0;y0;z0) і координати точки, що належить сфері M(xM;yM;zM).
Запишемо формулу для знаходження радіуса сфери – відстань між центром сфери O(0;0;0) і точкою, що належить сфері M(6;2;-3):
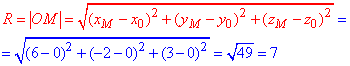
Так як центр знаходиться в початку координат то отримаємо канонічне рівняння сфери з радіусом R=7:
x2+y2+z2=49.
3) Відомі координати центра сфери O(x0;y0;z0) і рівняння дотичної площини a*x+b*y+c*z+d=0.
Знайдемо радіус сфери через відстань від центра сфери (1;4;-7) до точки дотику з площиною 6x+6y-7z+42=0 з нормальним вектором (6;6;-7) (значення беремо з р-ня площини):
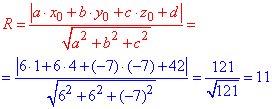
Формула не складна і після обчислень радіус рівний R=7.
Складаємо рівняння сфери з центром у заданій точці (1;4;-7) і R=11:
(x-1)2+(y-4)2+(z+7)2=121.
Запам'ятайте або випишіть наведену формулу, в плані розрахунків вона не складна.
4) Нехай маємо координати центра сфери O(x0;y0;z0) і дотичну до сфери вісь Oz.
Знайдемо радіус сфери як відстань від центра сфери (6;-8;3) до точки дотику K(0;0;3) з віссю аплікат - Oz за формулою
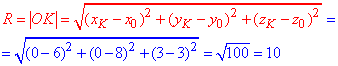
За відомим центром у точці (6;-8;3 і радіусом R=10 записуємо рівняння сфери:
(x-6)2+(y+8)2+(z-3)2=100.
Задача 6.1.2 Складіть рівняння описаної навколо трикутної піраміди ABCD сфери, якщо відомо координати вершин піраміди A(2;0;0), B(0;5;0), C(0;0;3),D(0;0;0).
Розв'язання: Оскільки трикутна піраміда ABCD вписана у сферу, то її вершини належать сфері. Тому відстань від центра сфери O(x0;y0;z0) до вершин піраміди однакова і є радіусом сфери R. Запишемо відстань від центру до точки A(2;0;0):
.
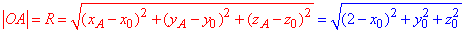Запишемо відстань від точки O(x0;y0;z0) до точки B(0;5;0):
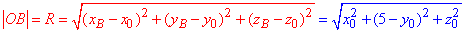Запишемо відстань від точки O(x0;y0;z0) до точки C(0;0;3):
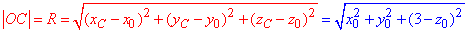
Запишемо відстань від точки O(x0;y0;z0) до точки D(0;0;0):
Прирівняємо відстань |OD|2 з кожною іншою, таким чином складемо систему трьох рівнянь з трьома невідомими:
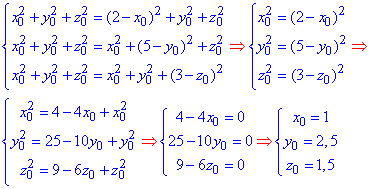
звідси остаточно отримаємо координати центра сфери O(x0;y0;z0)=(1;2,5;1,5).
Обчислимо радіус сфери за формулою:
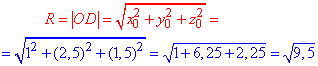
За наведеними на початку статті формулами складаємо рівняння сфери з центром у точці О(1;2,5;1,5) і радіусом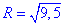 
:
(x-1)2+(y-2,5)2+(z-1,5)2=9,5
Задача 6.1.3 Визначте центр та радіус сфери:
а) x2+y2+z2-6x+8y+2z+10=0.
Розв'язання: Тут необхідно звести рівняння сфери до канонічного вигляду (методом виділення повних квадратів):
Перше рівняння при виділенні квадратів перетвориться наступним чином
x2-6x+9+y2+8y+16+z2+2z+1-9-16-1+10=0,
(x-3)2+(y+4)2+(z+1)2-16=0,
(x-3)2+(y+4)2+(z+1)2=42.
Отримали сферу з центром у точці O(3;-4;-1) та радіусом R=4.
б) x2+y2+z2+2x-4y-4=0;
Розв'язання: Доповнюємо квадратичні вирази до повних квадратів, а щоб компенсувати це від вільного члена віднімаємо квадрати сталих
x2+2x+1+y2-4y+4+z2-1-4-4=0,
(x+1)2+(y-2)2+z2-9=0,
(x+1)2+(y-2)2+z2=32.
Кінцеве рівняння описує сферу з центром O(-1;2;0) і радіусом R=3.
в) x2+y2+z2-6x+10=0;
Розв'язання:Виділимо повні квадрати у залежності
x2-6x+9+y2+z2-9+10=0,
(x-3)2+y2+z2+1=0,
(x-3)2+y2+z2=-1.
Отримали, сферу у якої квадрат радіуса від'ємний, а це значить, що маємо справу з комплексними числами.
i2=-1, R=i.
Отримали уявну сферу з центром в O(-1;2;0) і радіусом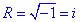 
.
г) x2+y2+z2-4x+12y-2z+41=0;
Розв'язання: Виділяємо повні квадрати і зводимо рівняння до канонічного вигляду
x2-4x+4+y2+12y+36+z2-2z+1-4-36-1+41=0,
(x-2)2+(y+6)2+(z-1)2=0.
Маємо окремий випадок «сфери» з центром O(2;-6;1) і радіусом R=0, що означає сфера вироджена в точку.
д) 36x2+36y2+36z2-36x+24y-72z-95=0.
Розв'язання: Тут слід бути уважними оскільки перед змінними маємо множники відмінні від одиниці. При зведенні до повних квадратів отримаємо
36x2+36y2+36z2-36x+24y-72z-95=0
36(x2-x+1/4)-36/4+36(y2+2/3*y+1/9)-36/9+36(z2-2z+1)-36-95=0,
36(x-1/2)2+36(y+1/3)2+(z-1)2-9-4-36-95=0,
36(x-1/2)2+36(y+1/3)2+(z-1)2-144=0,
(x-1/2)2+(y+1/3)2+(z-1)2=144/36=4.
Не забувайте вкінці обчислень нормувати рівняння на множник при "дужках". Задане рівняння описує сферу з центром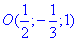 
і радіусом R=2.
Будьте уважні в подібних завданнях!
Задача 6.1.4 Запишіть рівняння сфери, що проходить через три точки (3;1;-3), (-2;4;1), (-5;0;0) і її центр лежить на площині 2x+y-z+3.
Розв'язання: Завдання не з простих, тому спробуйте вивчити алгоритм розрахунків.
З курсу математики відомо, що відстань від центра сфери O(x0;y0;z0) до кожної заданої точки є постійною і рівна радіусу сфери R.
Запишемо радіус в кожному із випадків за формулою відстані між двома точками.
Таким чином від центра O(x0;y0;z0) до першої точки A(3;1;-3) матимемо:
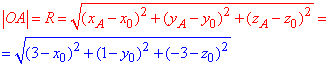
Далі розписуємо формулу відстані від точки O(x0;y0;z0)до точки B(-2;4;1):
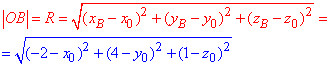
І наостанок віддаль до точки C(-5;0;0):
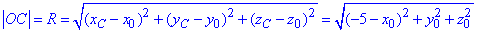
Подальші роздуми приводять до висновків:
оскільки центр сфери O(x0;y0;z0) належить заданій площині, тому можемо записати її рівняння у вигляді
2x0+y0-z0+3=0,
звідки виражаємо одну зі змінних z0=2x0+y0+3 (*).
Прирівняємо відстань |OC|2 з кожною іншою + врахуємо рівняння площини(*), таким чином дістанемо систему трьох рівнянь з трьома невідомими. Нижче наведені обчислення системи трьох рівнянь, яка при розписанні спрощується до лінійних
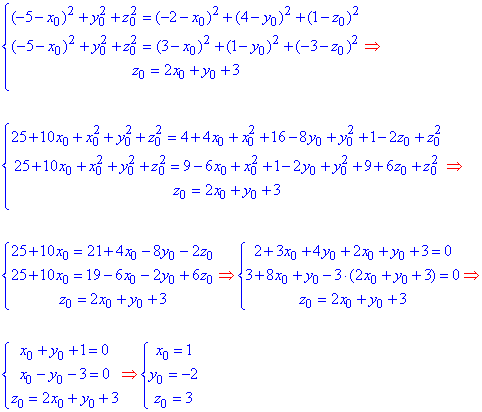
Знайдені координати центра сфери O(1;-2;3) підставляємо в будь-яке із рівнянь відстані та .
обчислюємо радіус сфери:
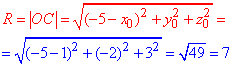
Він рівний R=7, звідси R2=49.
Скласти рівняння сфери при відомому центрі O(1;-2;3) і радіусі досить просто:
(x-1)2+(y+2)2+(z-3)2=49.
Перегляньте уважно відповідь та запам'ятайте хід обчислень.
Задача 6.1.5 Запишіть рівняння сфери, що проходить через чотири точки (1;-2;-1), (-5;10;-1), (4;1;11), (-8;-2;2).
Розв'язання: Як Вам відомо, відстань від центра сфери до кожної точки на поверхні є сталою, яка характеризує радіус сфери.
Як і в попередньому завданні, складаємо рівняння відстані від центру до заданих точок. Для першої A(1;-2;-1) отримаємо:
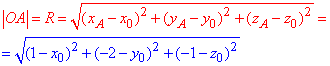
Для другої точки B(-5;10;-1) наступне значення:
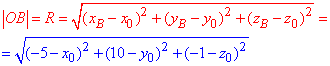
Точка C(4;1;11) від центру віддалена на |OC|:
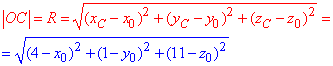
Відстань від четвертої точки D(-8;-2;2) до центру сфери рівна:
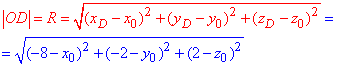
На відміну від попереднього прикладу немаємо площини, проте її компенсовує ще одна точка на сфері.
Для простоти обчислень прирівняємо квадрат відстані |OA|2 з кожною іншою і складемо систему трьох рівнянь для визначення трьох невідомих. Усі перетворення, які при цьому виконуємо можна записати формулами
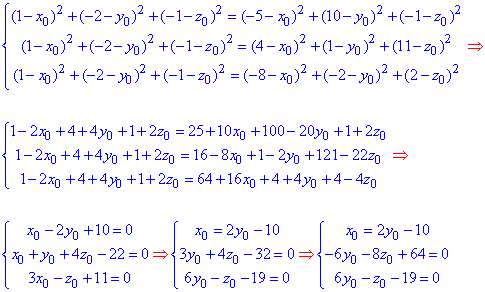
З останньої системи рівнянь отримали наступні координати центру сфери O(-2;4;5).
Підставляємо в одне з рівнянь та обчислюємо радіус сфери:
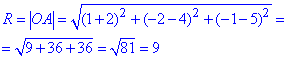
Він рівний R=9.
Маємо все необхідне для складання рівняння сфери:
(x+2)2+(y-4)2+(z-5)2=81.
Задача 6.1.6 Запишіть рівняння сфери радіуса R, яка дотикається:
а) до трьох координатних площин;
б) до трьох координатних осей.
Розв'язання:
а) Прямокутна декартова система координат має вісім октантів. Якщо в кожен із них помістити сферу, яка буде перпендикулярна до трьох площин, то координати центра сфери запишуться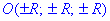 
, то рівняння сфери матиме вигляд.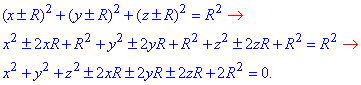 
Слід відмітити, що знак «мінус» буде стояти залежно від того, в якому октанті розміщається сфера.
Він може бути присутній при будь-якому множнику, подумайте чому так?
б) Рівняння сфери, яка дотикається до осей в першому октанті матиме вигляд
(x-a)2+(y-a)2+(z-a)2=R2.
При цьому, якщо точка належить осі, то її координати рівні, наприклад (a;0;0).
При підстановці в попереднє рівняння отримаємо
(a-a)2+(0-a)2+(0-a)2=R2,
2a2=R2,
a2=R2/2.
Добувши корінь квадратний отримаємо, що координати центра сфери для різних октантів можна записати формулою
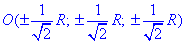
Підставимо центр O в рівняння сфери та розпишемо
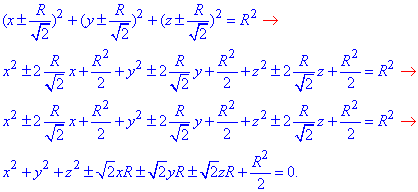
Тут також знак "мінус" входить у відповідності до того, в якому октанті розглядаємо сферу.
Задача 6.1.7 З'ясуйте, як розташована точка A(2;-1;3) стосовно кожної зі сфер:
а) (x-3)2+(y+1)2+(z-1)2=4;
Розв'язання: Для обчислення прикладів Ви повинні знати наступні правила:
- Якщо (xA-x0)2+(yA-y0)2+(zA-z0)2>R2, то точка знаходиться ззовні сфери.
- Коли виконується умова (xA-x0)2+(yA-y0)2+(zA-z0)2=R2, то точка знаходиться на (поверхні) сфери.
- При (xA-x0)2+(yA-y0)2+(zA-z0)2<R2 точка знаходиться всередині сфери.
Підставляємо координати точки в перше із заданих рівнянь
(2-3)2+(-1+1)2+(3-1)2=1+0+4=5>4=R2.
Маємо першу умову, тому робимо висновок, що точка A(2;-1;3) знаходиться ззовні заданої сфери;
б) (x+14)2+(y-11)2+(z+12)2=625;
Розв'язання:Обчислюємо відстань
(2+14)2+(-1-11)2+(3+12)2=256+144+225=625=R2.
Отримали, що точка A(2;-1;3) знаходиться на поверхні сфери.
в) (x-6)2+(y-1)2+(z-2)2=25.
Розв'язання:Підставляємо точку у рівняння
(2-6)2+(-1-1)2+(3-2)2=16+4+1=21<625=R2.
За третьою ознакою точка A(2;-1;3) знаходиться всередині сфери.
Задача 6.1.8 Обчисліть найкоротшу відстань від точки A до заданої сфери:
а) A(-2;6;-3),x2+y2+z2=4.
Розв'язання: Завдання не настільки важке, як виглядає на перший погляд.
Вам лише потрібно знати, що найкоротша відстань d від точки A(xA;yA;zA) до сфери з центром O(x0; y0; z0) і радіусом R рівна різниці між відстанню від точки до центра сфери |OA| і радіусом сфери R:
d=|OA|-R.
Рівняння сфери x2+y2+z2=4 має канонічний вигляд, центр якої в початку координат O(0; 0; 0) і радіусом R=2.
Спершу знаходимо відстань від точки A(-2;6;-3) до точки O(0; 0; 0) :
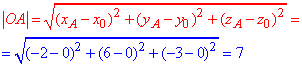
Найкоротшу відстань від точки A(-2;6;-3) до заданої сфери обчислюємо згідно формули:
d=|OA|-R=7-2=5.
Ось така легка схема обчислення задач.
б) A(9;-4;-3), x2+y2+z2+14x-16y-24z+241=0.
Розв'язання: Спершу необхідно в рівнянні сфери виділити повні квадрати, щоб знати реальне положення центру та сам радіус.
x2+14x+49+y2-16y+64+z2-24z+144-49-64-144+241=0,
(x+7)2+(y-8)2+(z-12)2=42.
Такий запис легко читати - сфера з центром O(-7;8;12) і радіусом R=4.
Відстань від точки A(9;-4;-3) до центра сфери O(-7;8;12) рівна:
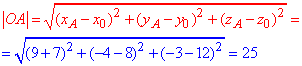
Знаходимо найкоротшу відстань від точки A до сфери:
d=|OA|-R=25-4=21.
в) A(1;-1;3), x2+y2+z2-6x+4y-10z-62=0.
Розв'язання: Виражаємо повні квадрати у рівнянні
x2-6x+9+y2+4y+4+z2-10z+25-9-4-25-62=0,
(x+3)2+(y+2)2+(z-5)2=102.
Сфера з центром в O(3;-2;5) і радіусом R=10.
Обчислюємо відстань від точки A до центра сфери:
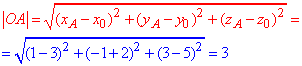
Тоді найкоротша відстань від точки A(1;-1;3) до сфери визначається з формули:
d=||OA|-R|=|3-10|=|-7|=7.
Знак "мінус" означає, що точка A знаходиться всередині заданої сфери, це не важко уявити.
Задача 6.1.9 Визначте, як розташована пряма стосовно сфери:
а)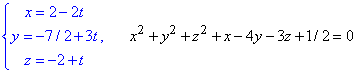 
Розв'язання: Щоб визначити розташування прямої (в просторі) відносно сфери, необхідно підставити параметричні рівняння прямої в рівняння сфери і обчислити дискримінант D квадратного рівняння: Далі можливі три варіанти:
- Якщо D2>0, то квадратне рівняння має два різних (дійсних) корені, тому пряма проходить через сферу у двох різних точках.
- Якщо D2=0, то квадратне рівняння має один корінь, тому пряма перетинає сферу у двох дійсних точках, що збігаються і є дотичною до цієї сфери.
- Якщо D2<0, то квадратне рівняння не має (дійсних) коренів, тому пряма
Покажемо, як виглядає аналіз прикладів на практиці.
x=2-2t, y=-7/2+3t, z=-2+t - рівняння прямої (в просторі) заданої параметрично.
x2+y2+z2+x+4y-3z+ 1/2=0 - задана сфера.
Підставимо параметризований запис прямої в рівняння заданої сфери та зводимо останнє до вигляду квадратного рівняння:
(2-2t)2+(-3,5+3t)2+(-2+t)2+2-2t+4(-3,5+3t)-3(-2+t)+ 1/2=0;
4-8t+4t^2+12,25-21+9t^2+4-4t+t^2+2-2t+14-12t+6-3t+0,5;
14t^2-50t+42,75=0.
Знаходимо дискримінант рівняння
D^2=50^2-4*14*42,75=2500-2394=106>0.
За першою ознакою пряма перетинає сферу у двох дійсних точках.
Задача 6.1.9 З'ясувати як розміщена пряма стосовно сфери:
б)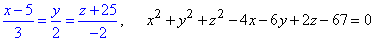 
Розв'язання: Перше з двох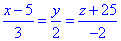
- канонічне рівняння прямої (в просторі), його ще потрібно перетворити до параметричного виду.
Друге рівняння x2+y2+z2+x+4y-3z+ 1/2=0 - задає сферу.
Приведемо рівняння прямої до параметричного вигляду:
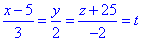
тобто x-5=3t, y=2t, z+25=-2t,
отримали x=5+3t, y=2t, z=-25-2t - параметричне рівняння прямої (в просторі).
Підставимо рівняння прямої в формулу для сфери:
(5+3t)2+(2t)2+(-25-2t)2-4(5+3t)-6*2t+2(-25-2t)-67=0;
25+30t+9t2+4t2+625+100t-+4t2-20-12t-12t-50-4t-67=0;
17t2+102t+513=0.
Обчислюємо квадрат дискримінанту квадратного рівняння
D2=1022-4*17*513=10404-34884=-24480<0.
За третьою ознакою пряма не перетинає задану сферу, а проходить повз неї.
Задача 6.1.9 Визначте як розміщена пряма по відношенню до сфери:
в)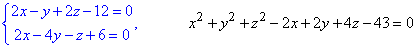 
Розв'язання: Перше рівняння описує пряму через перетин двох площин. Друге описує сферичну поверхню.
Перш за все нам необхідно рівняння прямої (в просторі) перевести в параметричну форму запису.
Для цього знайдемо напрямний вектор площини і точку, що належить прямій.
Напрямний вектор прямої в просторі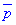 
– це векторний добуток 
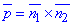двох нормальних векторів площин 
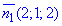і 
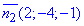, що утворюють пряму при перетині. Їх значення виписуємо як відповідні множники при "x,y,z".
Векторний добуток знаходимо за формулою
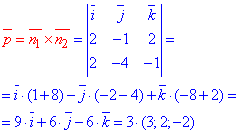
Знайдемо точку, що належить прямій (в просторі), для цього виберемо одну з координат (нехай x=0) та підставимо у систему рівнянь:
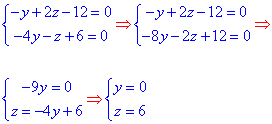
Отож точка M(0;0;6) належить прямій. Тому з врахуванням векторного добутку матимемо
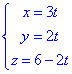
- рівняння прямої (в просторі) заданої параметрично.
Далі, за відомою з попереднього пункту схемою, підставимо параметризовані координати прямої в рівняння сфери:
(3t)^2+(2t)^2+(6-2t)^2-2*3t+2*2t+4(6-2t)-43=0;
17t2-34t +17=0 або t2-2t+1=0.
Дискримінант квадратного рівняння
D2=22-4*1*1=4-4=0.
Отож, пряма перетинає задану сферу у 2 дійсних точках, що збігаються, тобто є дотичною до сфери.
Задача 6.1.10 Запишіть рівняння площин, які проходять через пряму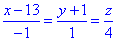 
і дотикаються до сфери
x2+y2+z2-2x-4y-6z-67=0.
Розв'язання: Запишемо рівняння площини з нормальним вектором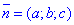 
і точкою M0(x0; y0; z0):
a(x-x0)+ b(y-y0)+c(z- z0)=0.
Оскільки пряма з точкою M0(-13; -1;0) належить площині, то рівняння площини набуде вигляду:
a(x-13)+ b(y+1)+c(z- z0)=0. (*).
Запишемо рівняння заданої сфери в канонічному вигляді:
x2-2x+1+y2-4y+4+z2-6z+9-1-4-9-67=0;
(x-1)2+(y-2)2+(z-3)2=92 - рівняння сфери з центром O(1; 2;3) і радіусом R=9.
Запишемо рівняння прямої (в просторі) з напрямним вектором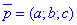 
, що проходить через центр сфери O (ця пряма буде перпендикулярна до шуканої площини, а її напрямний вектор 
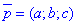- перпендикулярний до напрямного вектора заданої прямої 
):
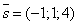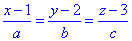
Умова перпендикулярності прямих:
-1*a+1*b+4*c=0;
a-b-4c=0. (1)
Знайдемо відстань від точки O(1; 2;3) до площини a(x-13)+ b(y+1)+c(z- z0)=0:
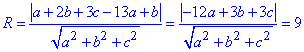
Перенісши корінь із знаменника в праву частину та спростивши на трійку, отримаємо
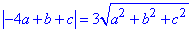
(-4a+b+c)2=9(a2+b2+c2).
Довизначимо одну з сталих, нехай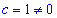 
, тоді
(-4a+b+1)2=9(a2+b2+c2);
16a^2+b^2-8ab-8a+2b+1=9a^2+9b^2+9;
7a^2-8b^2-8ab-8a+2b-8=0 (2).
Запишемо систему двох рівнянь (1) і (2) (при c=1):
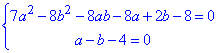
звідси
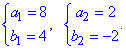
Отримали нормальні вектори прямих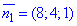 
і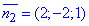 
.
Зазначимо, що ми прийняли координату с=1, оскільки для довільної відмінної від нуля сталої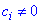 
вектори 
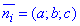будуть компланарні, а при с=0 маємо нульовий вектор a=b=0 (це випливає із системи рівнянь (1) і (2)), чого не може бути.
Підставимо ці вектори у співвідношення (*).
Рівняння шуканих площин запишемо формулами:
8(x-13)+4(y+1)+z=0 або 8x+4y+z-100=0;
2(x-13)-2(y+1)+z=0 або 2x-2y+z-28=0.
Задача 6.1.11 Знайдіть рівняння сфери, яка проходить через початок координат і через коло
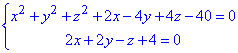
Розв'язання: Щоб записати рівняння сфери необхідно мати:
- координати центра і радіус сфери;
- координати центра сфери і точки, що належить сфері;
- чотири точки, що належать сфері.
З умови задачі маємо першу точку, що належить сфері A(0;0;0).
Із заданого рівняння кола (перетин сфери і площини), яке належить шуканій сфері, знайдемо ще три точки, що належить колу, а, отже, і шуканій сфері. Для z=0 маємо
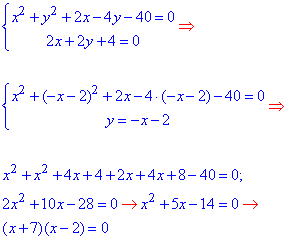
Отримали дві точки B(7;-9;0) і С(2;-4;0).
Для z=4 маємо
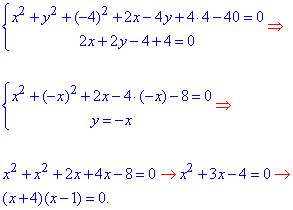
Отож отримали ще дві точки D(1;-1;4), E(-4;4;4).
Через чотири точки A,C,D,E запишемо рівняння шуканої сфери.
Для цього знайдемо координати центра і радіус сфери. Запишемо відстань від точки O до точки A:
Далі знайдемо відстань від точки O до точки C:
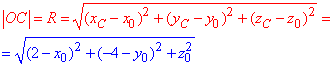Від початку координат до точки D(1;-1;4) відстань рівна:
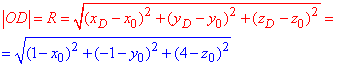
Останнє значення відстані між точками O до точки E(-4;4;4) знаходимо за правилом:
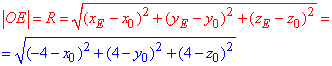
Прирівняємо відстань |OA|2 з кожною іншою, таким чином утворимо систему трьох лінійних рівнянь з трьома невідомими:
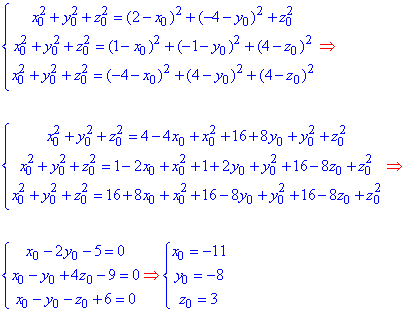
звідси x0=-11, y0=-8; z0=3. Обчислюємо радіус сфери:
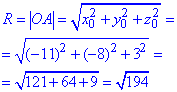
та підставляємо всі знайдені значення в формулу сфери
(x+11)2+(y+8)2+(z-3)2=194 або x2+y2+z2+22x+16y-6z=0.
На цьому пояснення до завдання завершені і переходимо до розгляду наступного прикладу.
Задача 6.1.12 Знайдіть рівняння сфери, яка проходить через коло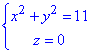
і дотикається до площини x+y+z-5=0.
Розв'язання: Коло, яке належить шуканій сфері є перетином циліндра з віссю Oz і площиною z=0, тобто перпендикулярною до осі Oz. Тому центр кола лежить на одній прямій (осі Oz) з центром шуканої сфери. Координати центра кола S(0;0), тому координати центра шуканої сфери є O(0;0;z0).
Візьмемо точку на колі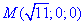 
, яка одночасно належить сфері, тоді
R2=(xM-x0)2+(yM-y0)2+(zM-z0)2,
тобто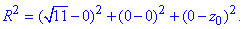 
Спростивши, матимемо
R2=11+z02 (1).
Відстань від точки (центра кола) O(0;0;z0) до площини x+y+z-5=0 є радіусом сфери R, оскільки задана площина є дотичною до сфери. Це дає підстави скласти другу залежність для радіуса
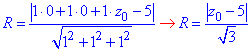
звідси R2=(z0-5)2/3 (2).
Прирівняємо вирази (1) і (2) та знайдемо координати центра і радіус сфери:
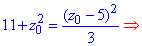
33+z02=z02-10z0+25;
2z02+10z0+8=0;
z0=-1 i z0=-4.
У відповідності до розрахунків отримаємо два кола з радіусами:
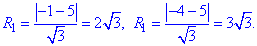
Записуємо рівняння сфери:
x2+y2+(z+1)2=12 і x2+y2+(z+4)2=27.
Подібних прикладів на сферу можна навести тисячі, всі вони та чи інакше пов'язані, а схеми обчислень подібні.
Вчіть формули та з користю застосовуйте на практиці!
