Сьогодні розглянемо добірку нових завдань на знаходження границі функції в точці. Почнемо з простих прикладів на підстановку значення, що найчастіше розглядають в 11 класі шкільної програми з математики. Далі зупинимося та проаналізуємо границі із невизначеностями, методи розкриття невизначеностей, застосуванням першої та другої важливих границь та їх наслідків. Наведені приклади повністю не охоплять всієї теми, але на багато питань внесуть ясність.
Знайти границю функції в точці:
Приклад 46. Границя функції в точці визначаємо підстановкою 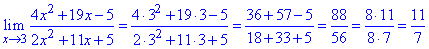
Так як знаменник дробу не перетворюється в нуль, то таке завдання під силу вирішити випускникові школи.
Приклад 47. Маємо частку поліномів, крім того знаменник не містить особливості.
Ще одне завдання, фактично за 11 клас.
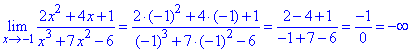
Приклад 48. Методом підстановки визначаємо границю функції 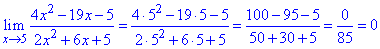
З умови легко слідує, що границя функції рівна двійціна якщо зміння прямує до нескінченності.
Приклад 49. Пряма підстановка x=2 показує, що границя в точці має особливість {0/0}. Це означає, що і чисельник і знаменник приховано містять (x-2).
Виконуємо розклад поліномів на прості множники, а далі спрощення на вказаний множник (x-2) .
Границю дробу, що залишиться знаходимо методом підстановки. 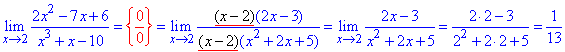
Приклад 50. Границя функції в точці має особивість типу {0/0}.
Позбуваємося різниці коренів домноженням на суму коренів (спряжений вираз), поліном розкладаємо, а далі перетворивши функцію знаходимо значення границі в одиниці.
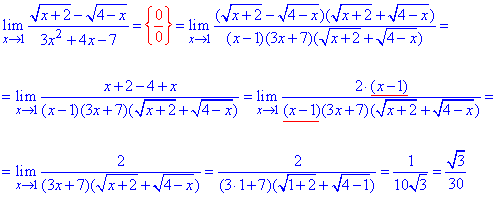
Приклад 51. Завдання на складні границі, оскільки досі ірраціональність відкривали помноживши на спряжений вираз. Тут же в знаменнику маємо корінь кубічний, тому потрібно зводити під формулу різниці кубів.
Все решта повторююється від умови до умови. Поліном розкладаємо на прості множники, спрощуємо на множник що вносить нулі та підстановкою знаходимо границю функції в точці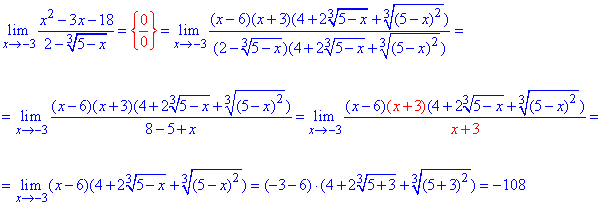
Приклад 52. Особливість виду {0/0} розкриваємо за допомогою першої важливої границі та її наслідків. Спершу різницю синусів розпишемо за тригонометричною формулою
sin(7x)-sin(3x)=2sin(2x)cos(5x).
Далі чисельник та знаменник дробу доповнюємо виразами, які необхідні для виділення важливих границь.
За правилами переходимо до добутку границь та оцінюємо вклад кожного множника.
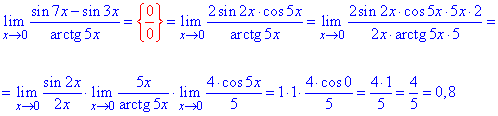
Тут використали першу важливу границю:
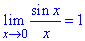
та наслідки з неї
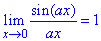 і
і
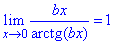
де a і b – довільні числа.
Приклад 53. Щоб розкрити невизначеність при змінній прямуючій до нуля використаємо другу важливу границю. Перетворюємо показник, щоб звести до експоненти, все що залишиться в граничному переході дасть степінь експоненти.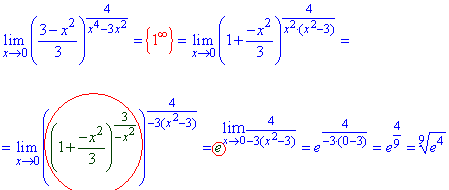
Тут використали наслідок з другої важливої границі:
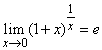
Обчислити границю функції в точці:
Приклад 54. Потрібно знайти границю функції в точці. Проста підстановка значення показує, що маємо ділення нулів.
Для її розриття розкладемо на прості множники поліноми та виконаємо спрощення на множник, що вносить особливість.
Проте чисельник далі містить (x+2), а це значить, що при x=-2 границя рівна нулю.
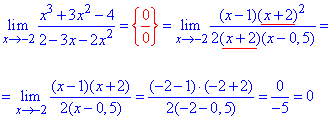
Приклад 55. Маємо дробову функцію, в чисельнику різниця коренів, в знаменнику – поліном. Пряма підстановка дає особливість виду {0/0}.
Змінна прямує до мінус одиниці, а це значить, що слід шукати та позбуватися особливостей (множника x+1).
Тому позбуваємося ірраціональності множенням на суму коренів, а квадратичну функцію розкладаємо на прості множники.
Після усіх спрощень методом підстановки визначаємо границю функції в точці
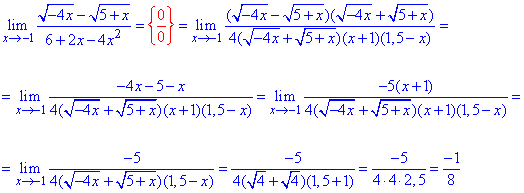
Приклад 56. З вигляду підграничної функції можна помилково зробити висновок, що потрібно застосувати першу границю, але обчислення показали, що все набагато простіше.
Спершу розпишемо суму синусів в знаменнику sin(2x)+sin(6x)=2sin(4x)*cos(2x).
Далі розписуємо tg(2x), та синус подвійного кута sin(4x)=2sin(2x)cos(2x).
Синуси спрощуємо і методом підстановки обчислюємо границю функції 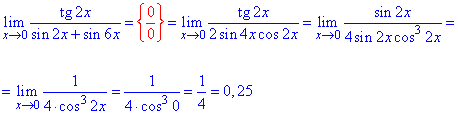
Приклад 57. Завдання на вміння використовувати другу важливу границю: суть полягає в тому, що слід виділити другу границю – експоненту.
Решта, що залишиться в показнику в граничному переході дасть степінь експоненти.
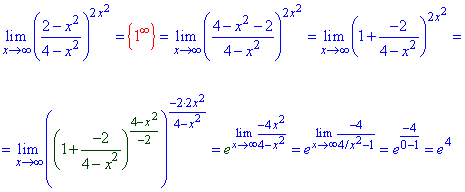
На цьому розбір завдань на границі функцій та послідовностей не завершується. На даний час підготовлено понад 150 готових відповідей на знаходження границь, тому вивчайте та діліться посиланнями на матеріал з одногрупниками.


