Серед прикладів границь функцій часто зустрічаються функції з коренями, які не завжди зрозуміло як розкривати. Найпростіше коли маємо приклад границі з кореневою функцією вигляду
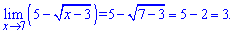
Розв'язання просте і зрозуміле кожному.
Труднощі виникають, якщо маємо наступні приклади функцій з коренями.
Приклад 1. Обчислити границю функції.
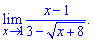
При прямій підстановці точки x=1 бачимо, що і чисельник і знаменник функції
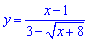
перетворюються в нуль, тобто маємо невизначеність 0/0.
Для розкриття такої невизначеності слід помножити вираз, що містить корінь на спряжений до нього та застосувати правило різниці квадратів. Для заданого прикладу перетворення будуть наступними
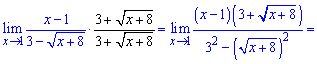
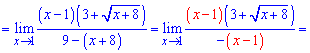
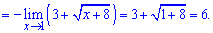
Границя функції рівна 6. Без наведеного правила її важко було б знайти.
Розглянемо подібні приклади обчислення границі на дане правило.
Приклад 2. Обчислити границю функції
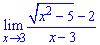
При підстановці x=3 отримаємо невизначеність виду 0/0.
Її розкриваємо множенням чисельника і знаменника на спряжене до чисельника.
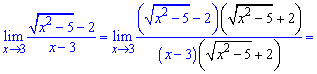
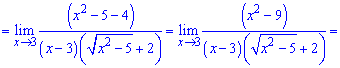
Чисельник розкладаємо за правилом різниці квадратів
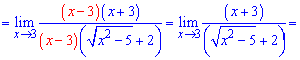
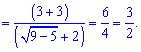
Ось так просто знайшли границю функції.
Приклад 3. Знайти границю функції
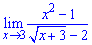
Бачимо, що маємо невизначеність виду 0/0.
Позбуваємося кореня в знаменнику
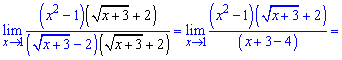
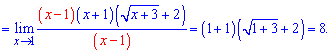
Границя функції рівна 8.
Тепер розглянемо інший тип прикладів, коли змінна прямує до безмежності.
Приклад 4. Обчислити границю
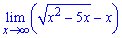
Маємо границю типу безмежність мінус безмежність. Множимо і ділимо на спряжений множник та використовуємо правило різниці квадратів
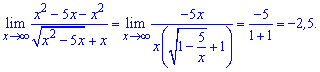
Границя функції рівна -2,5.
Приклад 5. Знайти границю функції
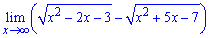
Границя еквівалента безмежність мінус безмежність
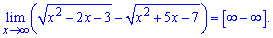 .
.
Помножимо і поділимо на спряжене та виконаємо спрощення

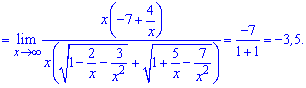
Винісши змінну в чисельнику та знаменнику можемо здогадатися до чого прямує функція.
Приклад 6. Чому рівна границя функції?
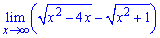
Маємо невизначеність виду безмежність мінус безмежність
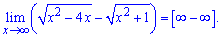
Виконуємо перетворення з кореневими функціями
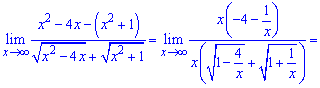
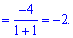
Границя рівна -2.
Добре перегляньте методику розкриття невизначеностей, алгоритм досить простий і допоможемо знайти складну границю.
Переглянути подібні матеріали


