Послідовність (bn) називають геометричною прогресією (г/п), якщо кожен її наступний член більший або менший від попереднього в q раз
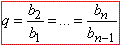
Формула суми геометричної прогресії
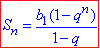
тут b1 перший член прогресії, q - знаменник.
Характеристичні властивості геометричної прогресії
Формула 1 використовують для суми скінченного ряду коли q≠1, суми геометричної прогресії

За формулою 2 обчислюємо суму нескінченно спадної геометричної прогресії (всього ряду n→∞).
Нагадаємо, що нескінченно спадною геометричною прогресією (bn) називають нескінченну геометричну прогресію, знаменник, якої за модулем менший від одиниці q<1, наприклад
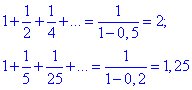
Далі наведені приклади зі шкільної програми, ЗНО тестів, олімпіад на знаходження суми геометричної прогресії.
Приклад 1 Знайдіть суму 4 членів геометричної прогресії, якщо b1=20, q=0,5.
Обчислення: Розв'яжемо завдання 3 способами
1 варіант
Застосуємо формулу загального члена прогресії для обчислення трьох членів прогресії
bn=bn-1q
b2=20•0,5=10;
b 3=10•0,5=5;
b4=5•0,5=2,5.
Додамо всі чотири числа та знайдемо суму прогресії
20+10+5+2,5=37,5
2 варіант
Для обчислення суми геометричної прогресії використаємо формулу
S4=(b4q-b1)/(q-1)=(2,5*0,5-20)/(0,5-1)=18,75/0,5=37,5
3 варіант
Застосуємо (1) формулу для знаходження суми г/п
Sn=b1(1-q^n)/(1-q)
S4=20(1-0,5^4)/(1-0,5)=20*0,9375/0,5=37,5
Як можна переконатися в кожному випадку отримали правильну відповідь, однак лише варіанти № 2, 3 дозволяють швидко знайти суму геометричної прогресії при великій кількості членів ряду.
Відповідь: 37,5.
Перетворення періодичного десяткового дробу на звичайний
Приклад 2 Записати число 0,(3) у вигляді звичайного дробу.
Обчислення:Розпишемо періодичний десятковий дріб через суму ряду
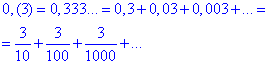
Числа 3/10, 3/100, 3/1000, ... утворюють нескінченну спадну геометричну прогресію зі знаменником q=1/10=0,1.
Суму нескінченно спадної прогресії обчислимо за формулою
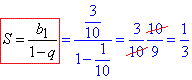
Таким чином, десятковому дробу 0,(3) відповідає звичайний 1/3.
Відповідь: 1/3.
ЗНО тести, сума геометричної прогресії
Приклад 21.10 Знайти 17+172+173+…+1720=
 Обчислення: Обчислити вираз 17+172+173+…+1720= означає знайти суму г/п, у якої
Обчислення: Обчислити вираз 17+172+173+…+1720= означає знайти суму г/п, у якої
b1=17 - перший член, q=17 - знаменник, n=20 - кількість членів цієї прогресії.
Обчислюємо суму 20 членів прогресії:
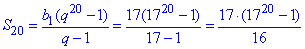
або
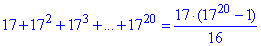
Відповідь: В.
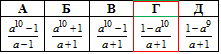
Приклад 21.19 Вираз 1-a+a2-a3+a4-…-a9, де a≠1, тотожно дорівнює виразу...
 Обчислення: В тестових відповідях маємо суми г/п.
Обчислення: В тестових відповідях маємо суми г/п.
Значить нам потрібно просумувати 1-a+a2-a3+a4-…-a9, де a≠1, b1=1 - перший член, q=-a - знаменник, n=10 - кількість членів цієї прогресії та порівняти з А-Д варіантами.
Підставляємо в формулу суми геометричної прогресі
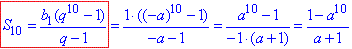
та спрощуємо до одного із заданих у тестах варантів
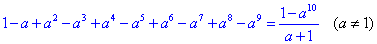
Відповідь: 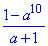 – Г.
– Г.
Приклад 21.22 Знайти суму
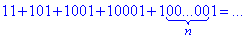
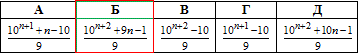
Обчислення: Щоб мати змогу порахувати суму подібних прогресій, розбивайте їх на скінченне число простих. Це легко виконати, і Ви завжди розумієте, що Ви рахуєте.
Для наведеного тестового прикладу розкладаємо суму на дві
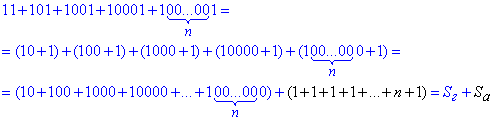
У перших дужках маємо геометричну прогресію, у якої b1=10 - перший член, q=10 - знаменник, n+1 - кількість членів г/п.
Тоді її сума:
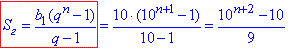
У других дужках маємо арифметичну прогресію, у якої a1=1 - перший член, d=0 - різниця, n+1 - кількість членів а/п.
Знаходимо її суму:
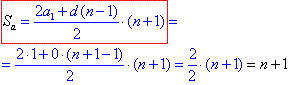
Сумуємо обидві прогресії 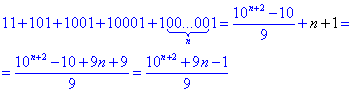
От і вся схема розрахунків.
Відповідь: 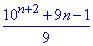 – Б.
– Б.
Приклад 21.31 Установити відповідність між геометричними прогресіями (bn) (1–4), заданими двома першими членами, та формулами суми n перших її членів (А–Д).
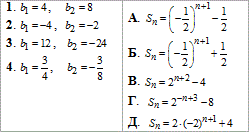 Обчислення: Запишемо алгоритм розв'язання таких прикладів на прогресію.
Обчислення: Запишемо алгоритм розв'язання таких прикладів на прогресію.
З аналізу умови бачимо, що задані сусідні члени геометричної прогресії, тому з обчисленням знаменника проблем не буде.
Він q рівній частці старшого до молодшого члена прогресії q=b2:b1.
Далі суму геометричної прогресії знаходимо за допомогою формули:
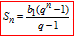 Після того виконуємо порівняння з тестовими відповідями А - Д.
Після того виконуємо порівняння з тестовими відповідями А - Д.
І так для всіх 4 пунктів.
1) b1=4, b2=8. q=b2:b1=8:4=2.
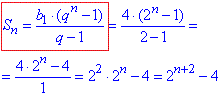
Отже, Sn=2n+2-4. 1 - В.
2) b1=-4, b2=-2.
q=b2:b1=-2:(-4)=1/2.
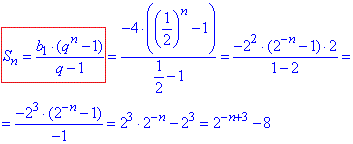
Звідси, Sn=2-n+3-8. 2 - Г.
3) b1=12, b2=-24.
q=b2:b1=-24:12=-2.
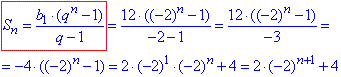
Отримали, Sn=2•(-2)n+1+4. 3 - Д.
4) Виконуємо обчислення суми прогресії
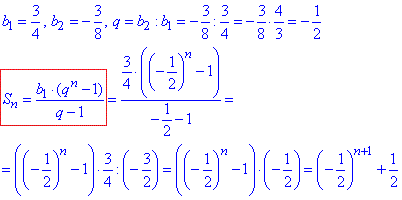
4 - Б.
Думаю, що після наведених відповідей Ви зможете розв'язати подібне завдання самостійно.
Приклад 21.33 Установити відповідність між заданими виразами (1–4) та їх сумами (А–Д).
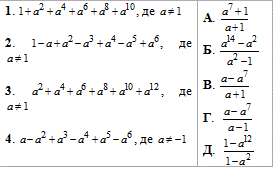
Обчислення: Доданки у заданих виразах утворюють геометричну прогресію (bn), це слідує з того, що члени послідовності змінюються за показниковим законом.
Тому записуємо перший член b1, обчислюємо знаменник q та кількість n членів (доданків у виразі).
Потім знаходимо суму геометричної прогресії за допомогою формули:
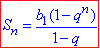
За наведеною схемою обчислюємо суму кожного ряду:
1) 1+a^2+a^4+a^6+a^8+a^10 де a≠1.
Маємо г/п, у якої b1=1, q=a^2 , n=6. Отже,
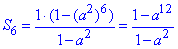
1 – Д.
2) 1-a+a^2-a^3+a^4-a^5+a^6, де a≠1.
Маємо г/п, у якої b1=1, q=-a, n=7. Отже,
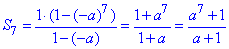
2 – А.
3) a^2+a^4+a^6+a^8+a^10+a^12, де a≠1.
Маємо г/п, у якої b1=a^2, q=a^2, n=6. Отже,
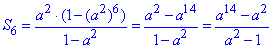
3 – Б.
4) a-a^2+a^3-a^4+a^5-a^6, де a≠1.
Маємо г/п, у якої b1=a, q=-a, n=6. Отже,
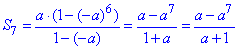
4 – В.
Ось так швидко розв'язуємо приклади на прогресію за допомогою простих і зрозумілих методик.
Далі розберемо готові відповіді до прикладів на суму нескінченно спадної геометричної прогресії та складні (№35-47) ЗНО тести.


