Всі формули різниці (кроку) арифметичної прогресії мають вигляд
d=a2-a1;
d=(an-a1)/(n-1).
Ще кілька формул можна отримати з формули суми арифметичної прогресії
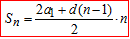
але виведення Ви побачити лише в тих завдання, де без цього не обійтися.
Загалом мало цікавих завдань на різницю прогресії є як на практичних в 9,10 класах, так і ЗНО тестах.
Далі розв'язані приклади на прогресію із ЗНО підготовки, в яких в умові потрібно знайти різницю прогресії.
Приклад 21.2 Арифметичну прогресію (an) задано формулою n-го члена an=4-8n.
Знайти різницю цієї прогресії.
А | Б | В | Г | Д |
8 | 4 | -2 | -4 | -8 |
Обчислення: Маємо an=4-8n - загальний член арифметичної прогресії (а/п), який заданий формулою,
тоді a1=4-8•1=-4 - перший член а/п;
a2=4-8•2=-12 - другий член а/п;
d=a2-a1=-12-(-4)=-12+4=-8 - різниця арифметичної прогресії.
Відповідь: -8 – Д.
Приклад 21.2a В арифметичній прогресії (an) a1=-2,7; a16=1,8.
Знайти різницю прогресії.
А | Б | В | Г | Д |
0,5 | 0,2 | 0,4 | -0,4 | 0,3 |
Обчислення: Використаємо формулу n-го члена:
an=a1+d(n-1).
Підставляємо значення з умови та розв'язуємо
1,8=-2,7+d(16-1),
15d=4,5;
звідси d=0,3 - різниця арифметичної прогресії.
Відповідь: 0,3 – Д.
ЗНО 2020. Завдання 27. В арифметичній прогресії (an) відомо, що a2-a5=7,8.
1. Визначте різницю d цієї прогресії.
2. Визначте перший член a1 цієї прогресії, якщо її третій член a3=-1,8.
Розв'язування: За формулою an=a1+d(n-1) розпишемо загальний член an арифметичної прогресії (АП):
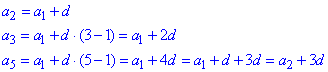
1. Обчислюємо різницю прогресії
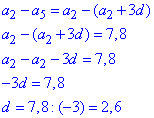
d=-2,6 - шукана різниця АП.
2. Розпишемо третій член АП через перший
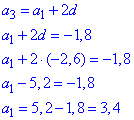
a1=3,4 - перший член (an).
Відповідь: -2,6; 3,4.
Приклад 21.24 Установити відповідність між арифметичними прогресіями (an) (1–4), заданими двома членами, та їх різницями (А–Д).
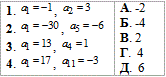
Обчислення: Формула для обчислення різниці (кроку) прогресії досить проста:
d=a2-a1=3-(-1)=4, 1 - Г.
У випадку великих номерів можемо вивести узагальнену формулу різниці прогресії:
an=a1+d(n-1), звідси d=(an-a1)/(n-1).
Отриману залежність використовуємо для розрахунку решти пунктів тестового завдання
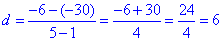2 - Д.
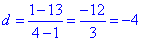3 - Б.
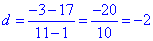4 - А.
Думаю такі тести вирішити Вам під силу. А тепер уявіть, що на ЗНО тестах чи контрольній Вам доведеться самостійно вирішувати наступне завдання.
Приклад 21.38 Знайти найбільше значення x, за яких числа x-1, 2x-1 і x2-5, записані в указаному порядку, утворюють арифметичну прогресію.
Обчислення: Оскільки числа x-1, 2x-1, x2-5 утворюють арифметичну прогресію, то (2x-1)-(x-1)=d і (x^2-5)-(2x-1)=d - різниця а/п.
Прирівнявши обидва вирази, знайдемо x:
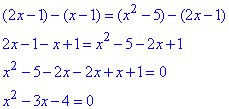
x1=-1; x2=4.
Робимо висновок, що x=4 - найбільше значення, за яких числа x-1, 2x-1, x^2-5, записані в указаному порядку, утворюють арифметичну прогресію.
Відповідь: 4.
Думаю з ходом обчислень Ви розібралися, а от чи самі змогли додуматися та правильно розв'язати, залишається відкритим питанням.
Поступово даний урок наповнимо цікавими задачами, а зараз переходьте до обчислення суми арифметичної прогресії та прикладів на геометричну прогресію.
