Показниковими називають рівняння в яких невідома величина міститься в показнику степеня, при цьому основа степеня не містить невідомої величини. Саме просте показникове рівняння ax=b розв'язують логарифмуванням x=log[a](b).
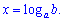
При розв'язуванні показникових рівнянь використовують властивість показників: якщо рівні вирази з однією і тією ж основою, то рівні показники степені, або основа дорівнює одиниці.
З рівності
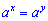
слідує x=y або a=1.
Деякі рівняння потребують заміни змінної, що веде до розв'язування степеневого рівняння. Для прикладу рівняння
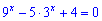
легко зводиться до квадратного, якщо зробити заміну
3x=y
При цьому вихідне рівняння набуде вигляду
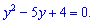
Після його розв'язку потрібно повернутися до заміни і розв'язати отримане рівняння.
Якщо показникове рівняння містить дві різні показникові функції (основи не зводяться до однієї), то виконують ділення рівняння на одну із основ у відповідній степені і перехід до показникового рівняння, що містить функцію з дробовою основою.
Шукаючи розв'язки показникових рівнянь слід пам'ятати, що показникова функція приймає лише додатні значення. Від'ємні значення або нулі заміненої змінної не беруться до розгляду.
На цьому необхідний теоретичний матеріал закінчується і переходимо до розгляду поширених прикладів.
Приклад 1.Розв'язати рівняння
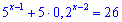
Розв'язок. Перепишемо рівняння в наступному вигляду
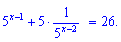
Другий доданок розпишемо, як добуток
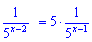
та зробимо заміну у рівнянні
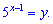
Вихідне рівняння перетвориться до наступного
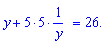
Областю допустимих значень буде дійсна множина за винятком точки y=0.
Помножимо залежнысть на y та переносимо выльний член в ліву сторону
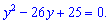
Отримали квадратне рівняння, корені якого знаходимо за теоремою Вієта. Не важко переконатися, що вони приймають значення
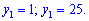
Повертаємося до заміни, та знаходимо розв'язки
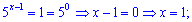
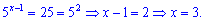
Виконуємо перевірку
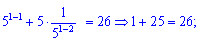
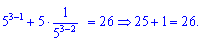
Отже обидва розв'язки x=1; x=3 задовольняють рівняння.
Приклад 2. Розв'язати рівняння
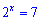
Розв'язок. Використовуючи одну з властивостей логарифма записуємо праву сторону рівняння у вигляді
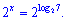
Прирівнявши показники, знаходимо
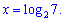
Отак вигядає правило про рівність показників при рівних осповах.
Приклад 3. Розв'язати рівняння
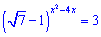
Розв'язок. Такого сорту приклади розв'язують логарифмуванням обох сторін, що приводить до зведення показникового рівняння до простого вигляду.
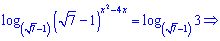
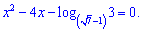
Отримане рівняння відносно змінної розв'язуємо через дискримінант
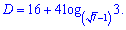
Корені рівняння набудуть значень
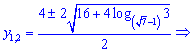
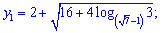
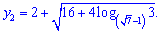
Іншого методу, який би дозволяв аналітично отримати розв'язки Ви не знайдете ні в інтернеті, ні на форумах.
Те що корені отримали громіздкі та ірраціональні - не проблеблема, головне що вони правильно знайдені.
Приклад 4. Розв'язати рівняння
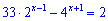
Розв'язок. Виконаємо деякі перетворення з показниками, щоб спростити рівняння
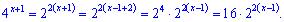
Еквівалентні значення підставимо у рівняння, в результаті отримаємо
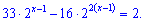
Виконуємо заміну змінних у показниковому рівнянні
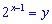
З врахуванням заміни переходимо до обчислень квадратного рівняння
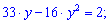
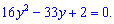
Знаходимо диискримінант
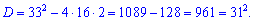
Отримане значення підставляємо у формулу коренів
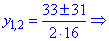
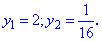
На цьому обчилення не завершені. Повертаємося до заміни змінних та знаходимо розв'язки показникового рівняння
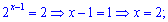
Тепер лише можна онстатувати, що завдання розв'язано.
Приклад 5.Розв'язати рівняння
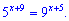
Розв'язок. Такого типу рівняння розв'язують за сталою основою. За основу класично беруть 10, однак, якщо взяти іншу (для даного прикладу 5 або 9) то розв'язок прийме компактніший вигляд.
Розглянемо обидва методи.
1. Прологарифмуємо обидві частини показникового рівняння
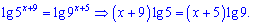
Розкриваємо дужки та групуємо доданки при невідомих. Вкінці виражаємо шукану веичину
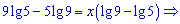
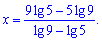
Отакий цікавий результат.
2. Прологарифмуємо обидві частини рівності за основою 9
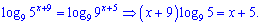
Групуючи доданки, що містять змінну, отримаємо
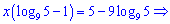
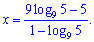
Обидва методи достатньо швидкі та ефективні. Відповіді хоч і не подібні, проте на інженерному калькуляторі чи будь-якому математичному пакеті можете переконатися, що вони рівні.
Приклад 6. Розв'язати рівняння
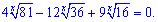
Розв'язок. Такого роду завдання розв'язують за наступною схемою. Показникове рівняння перетворюють до наступного вигляду
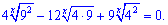
Усі доданки розділяємо на величину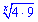 
, щоб звести до дробового вигляду
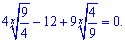
Після цього виконуємо заміну змінних
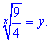
Далі Ви можете повправлятися самостійно. Якщо не маєте можливості, то перетворємо за наведеною вище схемою
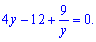
Множимо на змінну та розв'язуємо квадратне рівняння відносно нової змінної
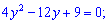
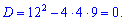
Дискримінант приймає нульове значення, отже корені рівняння співпадають
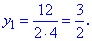
Повертаємося до заміни та розв'язуємо простеньке показникове рівняння
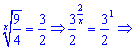
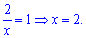
Хто не згідний, що дане рівняння просте, можете поставити "лайк" вкінці уроку.
Отримали єдиний розв'язок x=2.
Використовуйте наведену схему до подібних завдань і гарантовано отримаєте вірний результат.
Приклад 7. Розв'язати рівняння
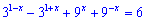
Розв'язок. На перший погляд рівняння досить складне і невідомо як його спрощувати, проте схема розв'язування даного прикладу та йому подібних досить проста та зрозуміла.
Виконаємо над рівнянням перетворення показників
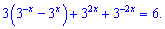
Далі необхідно показникову залежність перетворити до квадратного рівняння
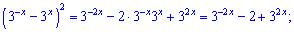
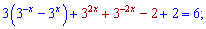
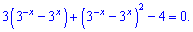
Повірте, що таке побачити по умові і виконати дуже важко для початківця, але з практикою Ви навчитеся розрізняти рівняння і яку підстановку слід застосовувати.
Виконаємо заміну змінних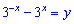 
та переписуємо рівняння у вигляді
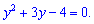
Обчислюємо дискримінант вадратного рівняння
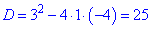
та корені рівняня
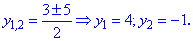
Повертаємося до зробленої заміни та знову отримуємо показникове
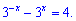
Ох і приклад дістався. Одні показникові рівняння розв'язуються через інші.
Отримане рівняння зводимо до квадратного, виконавши заміну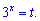 
В результаті прийдемо до квадратичної залежності
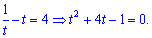
Розв'язуємо через дискримінант
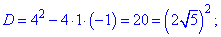
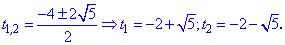
Повертаємося до заміни і визначаємо змінну x знову ж таки - з показникового рівняння (логарифмуванням)
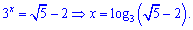
Друге значення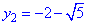 
розглядати не будемо, оскільки воно від'ємне, а показникова функція 
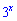всюди додатна.
Не забуваємо, що в нас є ще один корінь рівняння, який може внести свій вклад в кінцеву відповідь.
Розв'язуємо другу половину завдання
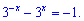
Використовуючи попередню заміну, отримаємо
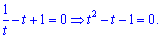
Через дискримінант
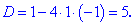
знаходимо корені рівняння
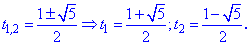
Перший корінь має зміст, другий – від'ємний і не підходить.
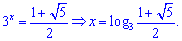
Отримали два розв'язки показникового рівняння
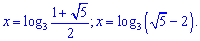
Отаке чудернацьке рівняння можуть придумати математии, щоб завалити Вас на тестах чи екзаменах.
Тож ставтися до на вчан ня відповідально і вдосконалюйте знання від простих до складних завдань.
Переглянути схожі матеріали:
- Прості показникові рівняння
- Розв'язки показникових рівнянь
- Логарифмічні та показникові рівняння та нерівності
- ГДЗ Алгебра 11 клас. Показникові рівняння
Добре розберіться з наведеними методами розв'язування показникових рівнянь, можливо деякі з них стануть в нагоді при проходженні ЗНО, екзамені чи контрольній роботі.
