Показникові рівняння на простих прикладах

Прості приклади на показникові рівняння дозволять оволодіти методикою їх розв'язування. Завдання не надто складні і будуть корисними для всіх хто вивчає показникові рівняння, готується до тестування, контрольних чи вступних іспитів.

Приклад 1. Розв'язати рівняння
(0,5)^х =.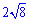
Розв'язання: Перетворимо праву сторону рівняння

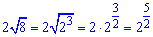
Рівняння перетвориться до спрощеного вигляду

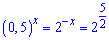
Основи рівні, тому прирівнюємо показники

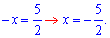
Ось такі прості обчислення.

Приклад 2. Розв'язати рівняння
(2/3)^х*(9/8^)х =27/64.
Розв'язання: Зведемо праву і ліву сторону показникового рівняння до однієї основи


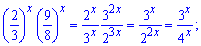
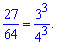
Спрощуємо рівняння і прирівнюємо показники

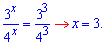
Розв'язок рівняння x=3.

Приклад 3. Розв'язати рівняння
5^2х-7^х-35*5^2х+35*7^х=0.
Розв'язання: Згрупуємо доданки, які містять множники 5^2х та 7^х.


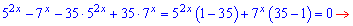
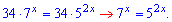
Останній запис показникового рівняння багато кого заводить в тупик. Важко знайти відповідь. Тоді, давайте перепишемо рівняння у вигляді

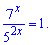
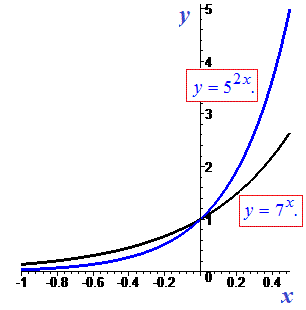
За властивостями показникових функцій розв'язок рівний нулю x=0. Тільки піднесенням до 0-го степеня можна отримати одиницю. Якщо не вірите - перегляньте графіки показникових функцій

Приклад 4. Розв'язати рівняння
14^х+2+5*14^х-1=2749.
Розв'язання: В подібних завданнях необхідно винести основу з найменшим показником. Для цього розпишемо рівняння до вигляду.




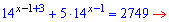
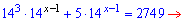
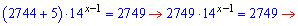
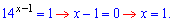
Тут більше нічого коментувати, бо і так все ясно з формул. Розв'язок показникового рівняння рівний одиниці.

Приклад 5. Розв'язати рівняння
(0,6)^х+2 =25/9 .
Розв'язання: Такого роду завдання слід розв'язувати за наступною схемою:
Обов'язково перетворити число 0,6 до дробового вигляду

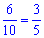
Далі вже поступають виходячи з умови, в нашому випадку перетворюємо праву сторону.

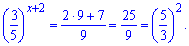
Прирівнюємо показники, попередньо змінивши знак в котромусь, щоб отримати однакові основи
x+2=-2; x=-2-2=-4.
Розв'язок рівняння x=-4.
Я бачите не важко обчислите і таке завдання.

Приклад 6. Розв'язати рівняння
(0,25)^х-1=2*sqrt(2)
Розв'язання: Зведемо показникове рівняння до однієї основи

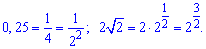
Підставимо перетворені записи в рівняння та розпишемо його



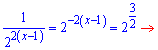
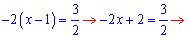
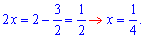
Розв'язок рівний 1/4.

Приклад 7. Розв'язати рівняння
(1,44)^х-4=6/5.
Розв'язання: Не одразу можна здогадатися, як спрощувати рівняння. Зведемо спочатку праву сторону до десятового запису 6/5=1,2.
Основу в лівій частині зводимо до значення 1,2

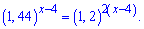
Після підстановки прирівнюємо показники при однакових основах

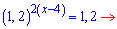
2(x-4)=1;
2x-8=1;
2x=9;
x=9/2=4,5.
Дещо розписавши отримаємо корінь показникового рівняння x=4,5.

Приклад 8. Розв'язати рівняння

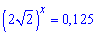
Розв'язання: Використовуємо основоположне правило для показникових рівнянь – звести вирази до однією основою. Виконаємо маніпуляції з основою


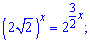
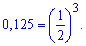
Підставляємо і прирівнюємо показники

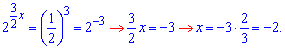
Розв'язок показникового рівняння рівний x=-2.

Приклад 9. Розв'язати рівняння 3^х-1+3^х-2+3^х-3=13.
Розв'язання: Розписуємо доданки так, щоб потім згрупувати ті, що мають однакові степені

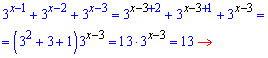
Подальші дії досить прості

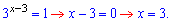
Розв'язок показникового рівняння рівний x=3.

Приклад 10. Знайти суму розв'язків рівняння

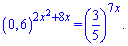
Розв'язання: Можна здогадатися, що прийдеться обчислювати квадратне рівняння. Але до нього, ще потрібно прийти. Для початку запишемо 0,6 у вигляді

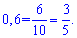
Підставимо у показникові рівняння

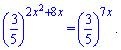
Тепер можна прирівняти степені при основах

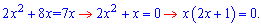
Розв'язки рівні x=0; x=-1/2.
Їх сума рівна 0-1/2=-0,5.
На цьому ознайомлення з можливими простими показниковими рівняннями завершено. Складніші приклади шукайте на сторінках сайту.

Переглянути схожі матеріали:

• Показникові рівняння
• Розв'язки показникових рівнянь
• ГДЗ Алгебра 11 клас. Показникові рівняння

Залишайтеся з нами і ми підготуємо Вас краще за репетиторів.