Решение множества показательных уравнений не обходится без замен, квадратных уравнений и сложных преобразований. Приведенные ниже примеры помогут Вам в этом быстро разобраться и научат решать самые сложные из них. Также Вы сможете выучить некоторые свойства логарифмов без которых показательные уравнения в простой способ не решить. Начнем с самых азов - теоретического материала об уравнениях.
Показательными называют уравнения в которых неизвестная величина содержится в показателе степени, при этом основа степени не содержит неизвестной величины. Самое простое показательных уравнения ax=b решают логарифмированием x=log[a](b).
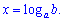
При решении показательных уравнений используют свойство показателей: если в уравнение степени с одной и той же основой то равные показатели степени или основание равно единице.
Из равенства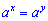 
следует 
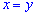или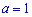 
.
Некоторые уравнения требуют замены переменной и сводится к решению степенного уравнения. Например уравнения
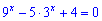легко сводится к квадратному если сделать замену
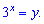При этом исходное уравнение примет вид
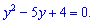После его решения нужно вернуться к замене и решить полученное уравнение.
Если показательной уравнение содержит две различные показательные функции ( основы не сводятся к одной) , то выполняют деления уравнения на одну из основ в соответствующей степени и переход до показательного уравнения которое содержит функцию с дробной основой.
Находя решения показательных уравнений следует помнить что показательная функция принимает только положительные значения. Отрицательные значения или нули замененной переменной не принимаются к рассмотрению.
На этом необходимый теоретический материал заканчивается и переходим к рассмотрению распространенных примеров.
Пример 1.Решить показательное уравнение
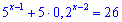
Решение. Перепишем уравнение к следующему виду
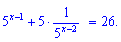
Второе слагаемое распишем как произведение
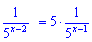
и сделаем замену в уравнении
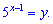
Исходное уравнение преобразуем к следующему
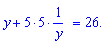
Областью допустимых значений будет действительная ось за исключением точки y=0.
Умножим его на y и переносим все в левую сторону
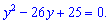
Получили квадратное уравнение корни которого находим по теореме Виета. Нетрудно убедиться что они принимают значения
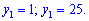
Возвращаемся к замене и находим решения
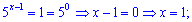
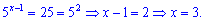
Выполняем проверку
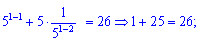
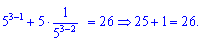
Итак оба решения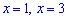 
удовлетворяют уравнению.
Пример 2. Решить показательное уравнение
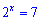
Решение. Используя одну из свойств логарифма записываем правую сторону уравнения в виде
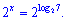
Приравнивая показатели находим
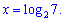
Пример 3. Решить уравнение
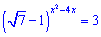
Решение. Такого сорта примеры решают логарифмированием обеих сторон что приводит к сведению показательного уравнения к простому виду.
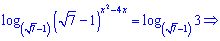
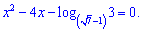
Полученное уравнение относительно переменной решаем через дискриминант
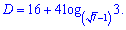
Корни уравнения приобретут значения
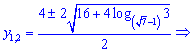
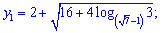
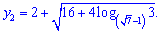
Другого метода позволяющего аналитически получить решения Вы не найдете ни в интернете, ни на форумах.
Пример 4. Решить уравнение
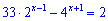
Решение. Выполним некоторые преобразования с показателями чтобы упростить уравнение
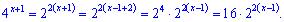
Эквивалентные значения подставим в уравнение, в результате получим
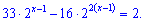
Выполняем замену
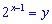
Уравнение превратится к квадратному
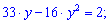
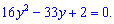
Вычисляем дискриминант
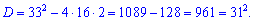
Найденное значение подставляем в формулу корней
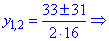
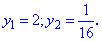
Возвращаемся к замене и находим
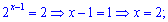
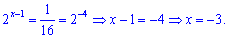
Задача решена.
Пример 5.Решить уравнение
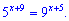
Решение. Такого типа уравнения решают с постоянной основой . За основу классически берут 10 , однако , если взять другую (для данного примера 5 или 9 ) то решение примет компактный вид
Рассмотрим оба метода.
1. Прологарифмируем обе части равенства
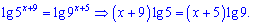
Раскрываем скобки и группируем слагаемые при неизвестных
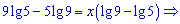
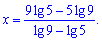
Такой интересный результат.
2. Прологарифмируем обе части равенства по основанию 9
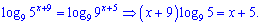
Группируя слагаемые содержащие переменную получим
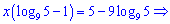
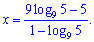
Оба метода достаточно быстрые и эффективные, для себя выбирайте который Вам больше подходит.
Пример 6.Решить уравнение
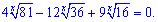
Решение.Такого рода задачи решают по следующей схеме. Показательное уравнения превращают к виду
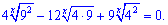
Все слагаемые разделяем на величину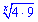 
чтобы свести к дробному виду
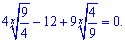
После этого выполняем замену
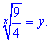
Уравнение переписываем в виде
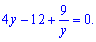
Умножаем на переменную и решаем квадратное уравнение
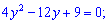
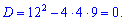
Дискриминант принимает нулевое значение, при етом корни уравнения совпадают
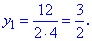
Возвращаемся к замене и решаем
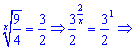
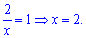
Итак x=2 - единственное решение.
Используйте приведенную схему в подобных задач и гарантированно получите верный результат.
Пример 7. Решить уравнение
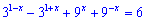
Решение. На первый взгляд уравнения достаточно сложное и неизвестно как его упрощать, однако схема решения данного примера и подобных довольно проста и интересна. Выполним над уравнением преобразования
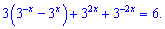
Нужно это уравнение преобразовать к квадратному
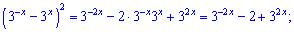
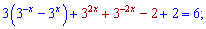
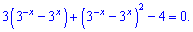
Выполним замену
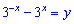
и перепишем уравнение в виде следуещого
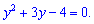
Вычисляем дискриминант
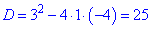
и корни уравнения
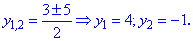
Возвращаемся к совершенной замене
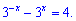
Такое уравнение сводим к квадратному, выполнив замену
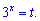
В результате получим
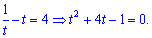
Решаем через дискриминант
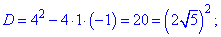
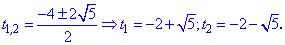
Возвращаемся к замене и определяем переменную x
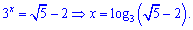
Второе значение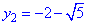 
рассматривать не будем, поскольку оно отрицательное, а показательная функция 
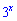всюду положительная.
Решаем вторую половину задачи
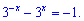
Используя предыдущую замену получим
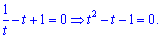
Дискриминант примет значение
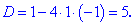
Находим корни уравнения
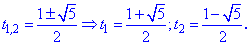
Первый корень имеет место бить, второй - отрицательный и не подходит.
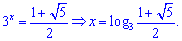
Получили два решения показательного уравнения
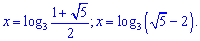
Хорошо разберитесь с приведенными методами решения показательных уравнений, возможно некоторые из них пригодятся при прохождении ВНО, экзамене или контрольной работе. Будьте внимательны при упрощении, первое время используйте подстановку для проверки результатов.
Похожие материалы:
