Комбіновані показникові нерівності

Продовжуємо розбирати показникові нерівності за програмою підготовки до ЗНО тестів. В попередніх статтях описані основні алгоритми розкриття показникових нерівностей, включаючи логарифмування, зведення до квадратних нерівностей та метод інтервалів. Сьогодні проаналізуємо відповіді до прикладів, які в степенях мають дробові функції, модулі, основи містять корені, при розкритті доводиться обчислювати квадратні рівняння, і т. д.
Аналіз таких прикладів навчить Вас багато нового, особливо учнів та студентів, які хочуть розібратися в темі самостійно.
Перш ніж аналізувати обчислення, перегляньте графіки та властивості показникових функцій

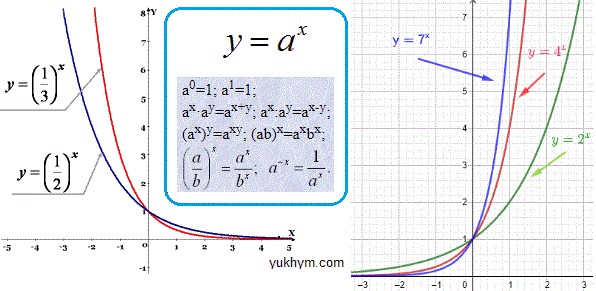
ЗНО підготовка. Показникові нерівності

Приклад 15.31 Розв'язати нерівність (2^x-8)(x²-4x+3)>0.
У відповідь записати добуток усіх натуральних чисел, які не є розв'язками нерівності.
Розв'язування: Розв'яжемо задану нерівність методом інтервалів.
Знайдемо корені рівняння:
(2^x-8)(x²-4x+3)=0.

Отримали один x₁=3 – корінь кратності 2 (два рази повторюється) та x₂=1.
Нанесемо отримані корені на числову пряму, розставимо знаки на кожному інтервалі, враховуючи кратність коренів і знак заданої нерівності:
(Якщо маємо корені парної кратності, то при переході через ці точки знаки на інтервалах не міняються).

x∈(1;3)∪(3;+∞) – розв'язок нерівності.
Випишемо усі натуральні числа, які не є розв'язками та знайдемо їх добуток:
1; 3.
1•3=3.
Відповідь:3.

Приклад 15.18 Розв'язати нерівність (1/2)^(|x|-1)<1/8.

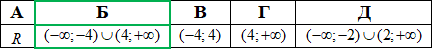
Розв'язування: Перетворюємо показникові вирази до спільної основи, а далі розписуємо рівняння з модулем. Не забувайте, що при основі меншій одиниці (1/2<1) при записі степенів при рівних основах знак потрібно змінити на протилежний

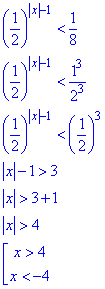
Далі методом інтервалів

знаходимо розв'язки нерівності x∈(-∞;-4)∪(4;+∞).
Відповідь:(-∞;-4)∪(4;+∞) – Б.

Шкільної підготовки за 10, 11 клас цілком достатньо, щоб розв'язувати приклади такого плану. Модулі та квадратні рівняння Ви вже вивчили, тут їх треба обчислювати поодинці, а вкінці результати об'єднати.

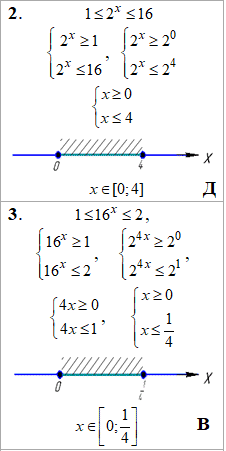
Приклад 15.24 Установити відповідність між нерівностями (1–4) та множинами їх розв'язків (А–Д).

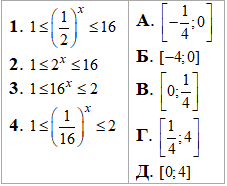
Розв'язування: Подвійні нерівності спершу зводимо до однієї основи, після чого розкриваємо за правилами для показникових функцій.
Результати перетворень та інтервали розв'язків наведені у таблиці:

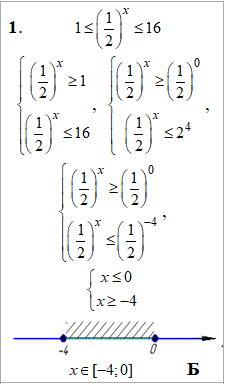
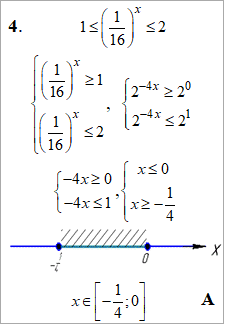
Приклад 15.34 Знайти найбільший цілий розв'язок нерівності 7^(x-5)>3^(x²+x-30).
Розв'язування: Основи нерівності, як і показники нерівні, тому застосуємо метод логарифмування. Оскільки основа більша за одиницю 3>1, то при логарифмуванні знак нерівності не зміниться. (При менших за одиницю основах значеннях логарифм від'ємний, тому в таких випадках при логарифмуванні слід змінювати знак нерівності.)

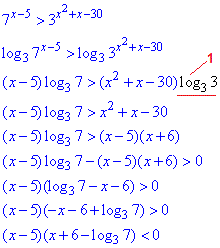
Логарифм основи рівний одиниці.
Наприкінці обидві частини нерівності помножили на -1, тому знак нерівності змінили на протилежний.

Корені знаходимо методом інтервалів
(x-5)(x+6-log₃7)=0,
x₁=5,
x₂=-6+log₃7 (x₂≈-4,22).
Будуємо числову вісь, наносимо точки та визначаємо інтервали знакосталості

x∈(-6+log₃7;5) – розв'язок нерівності.
Звідси, x=4 – найбільший цілий розв'язок нерівності.
Пам'ятайте, що при строгих нерівностях крайні точки не є розв'язками.
Відповідь:4.

Вчіть правила додавання та множення степенів, властивості показникових та логарифмічних функцій, без цього Ви не зможете розв'язати складніших завдань.

Приклад 15.35 Розв'язати нерівність

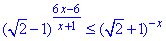
У відповідь записати найбільший розв'язок нерівності.
Розв'язування: Знаменник в показнику не повинен дорівнювати 0, звідси ОДЗ: x≠0.
За правилом різниці квадратів перетворимо вираз √2+1:

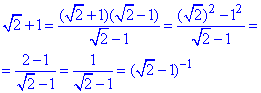
Прирівняємо степені

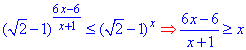
Основа менша одиниці 0<√2-1<1, тому знак нерівності змінили на протилежний.
Старайтеся оцінювати основи, які на Вашу думку, можуть бути меншими одиниці.
Розпишемо дробову нерівність

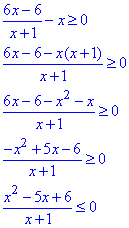
(обидві частини нерівності помножили на -1, тому знак нерівності змінили на протилежний)
Кінцеву формулу замінюємо системою нерівностей та розв'язуємо методом інтервалів

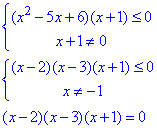
звідси x₁=2, x₂=3, x₃=-1.

x∈(-∞;-1)∪[2;3] – розв'язок нерівності.
Звідси x=3 – найбільший розв'язок.
Відповідь:3.

Приклад 15.37 Розв'язати нерівність

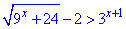
У відповідь записати найбільший цілий розв'язок нерівності.
Розв'язування: Перевіряємо вираз під коренем:
9^x+24>0 для будь-яких x (на розв'язок нерівності не впливає).
Щоб позбутися кореня квадратного, підносимо обидві частини до квадрату.
Далі групуємо подібні доданки

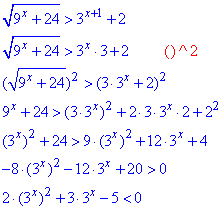
Заміна: 3^x=t, де t>0 зводить нерівність до квадратної
2t²+3t-5<0.
Корені відповідного квадратного рівняння знаходимо через дискримінант

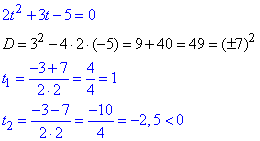
Враховуючи умову на заміну t>0, графічним методом визначаємо

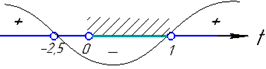
множину коренів квадратичної нерівності t∈(0;1).
Залишилося повернутися до заміни та обчислити прості показникові нерівності

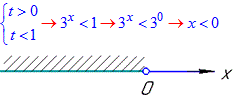
Нерівність виконується на інтервалі x∈(-∞;0).
Звідси, x=-1 – найбільший цілий розв'язок.
Відповідь:-1.

Приклад 15.42 Дано функції f(x)=2^x-8 і g(x)=x^2-4x+3.
1) Розв'язати рівняння g(x)/f(x)=0;
2) розв'язати нерівність f(x)•g(x)>0.
У відповідь записати добуток усіх натуральних чисел, які не є розв'язками нерівності.
Розв'язування: 1) Розв'яжемо рівняння: g(x)/f(x)=0, тобто
(x²-4x+3)/(2^x-8)=0.
В чисельнику маємо квадратне рівняння, яке прирівнюємо до нуля.
Друге рівняння виписуємо з умови, що знаменник дробу не рівний нулю

Звідси, x=1 – єдиний корінь рівняння g(x)/f(x)=0.

2) Розв'яжемо нерівність:
f(x)•g(x)>0, тобто (2^x-8)(x²-4x+3)>0.
Розпишемо нерівність методом інтервалів.
Для цього спершу визначимо розв'язки обох рівнянь:
(2^x-8)(x²-4x+3)=0.

Обидва рівняння мають один спільний корінь x₁=3, кратності 2 та x₂=1. Слід зазначити, що при переході "іксів" через корені парної кратності знак нерівності не змінюється.
Наносимо знайдені точки на числову пряму, далі шляхом підставлення, наприклад точки x=0 з'ясовуємо знаки нерівності
(2⁰-8)(0-0+3)=-24<0
На інтервалі (-∞;1) нерівність не виконується, нас цікавлять проміжки, де добуток буде додатним.
Тому переходимо на сусідні інтервали, правіше x=1 за виключенням точки x₁=3 нерівність виконується

Записуємо множину розв'язків нерівності x∈(1;3)∪(3;+∞).
Бачимо, що число 3 є єдиним натуральним числом, що не є розв'язками нерівності.
В умові потрібно знайти добуток таких чисел, тому нічого не залишається як вписати знайдене значення =3.
Відповідь:1) 1; 2) 3.

Щоб зрозуміти, як розв'язувати такі рівняння, а ще краще навчитися обчислювати самостійно потрібно розібрати десятки й сотні готових відповідей. На сайті на показникові вирази, рівняння та нерівності розв'язано понад 200 прикладів. Від Вас потрібно тільки бажання уважно все перечитати та вибрати для самоосвіти максимум корисної інформації.