Приклади на показникові рівняння та системи рівнянь досить часто важко спростити. Всі шукають допомоги в методичках, інтернеті , серед знайомих. Нижче наведені схеми розв'язування типових для практики прикладів на показникові рівняння. Їх Ви можете зустріти на контрольній, тестах, проходженні ЗНО з математики. Пояснення достатньо розписані, тож розбирайте і вибирайте корисний для себе матеріал.
Показникові рівняння середньої складності
Приклад 1. Розв'язати рівняння
2(2x+1)+2(2x+2)+2(2x)=28.
Розв'язання: Дехто вже мабуть подумав, що ми збираємося грузити складними завданнями і збирається покинути сторінку. Проте все з точністю до наоборот, це одне з простих рівнянь і з обчислень Ви скоро в цьому переонаєтесь.
Схема розв'язування подібних показникових прикладів: виносимо множник в найменшому степені за дужки
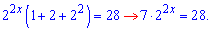
Подальші дії стануть ясними в ході самих обчислень. Як правило, показникові рівняння спрощується до найпростішого типу з якими практично усі знають, що робити. В нашому випадку
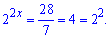
Далі якщо маємо рівні основи (2=2), то і показники мають бути рівні 2x=2; x=1. Ось і вся мудрість!
Однак на ній можна побудувати такі показникові рівняння, що голова почне боліти не тільки в студента, а й у викладача, якому прийдеться пояснювати біля дошки складне завдання. Тож не розслабляйтеся і уважно перегляньте наступні приклади.
Приклад 2. Знайти добуток розв'язків рівняння
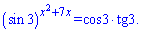
Розв'язання: Таке завдання під силу не кожному. Тут потрібно добре знати і тригонометрію і показникові рівняння. Перетворимо спочатку праву сторону
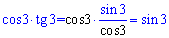
і вже бачимо, як розв'язувати показникове рівняння
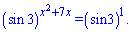
Записано в такому вигляді, оскільки не всі ще навчилися бачити показники. Прирівняємо степені і отримаємо квадратне рівняння
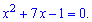
Далі залежить від ваших знань. Можна розв'язувати квадратне рівняння через дискримінант і шукати добуток розв'язків рівняння, а можна скористатися теоремою Вієте, що ми і зробимо. За нею добуток коренів рівний вільному члену, тобто (-1). Ось і всі обчислення для даного прикладу. І головне, вкінці не забувайте читати, що потрібно знайти, а то на контрольній багато з Вас сидять розгублені і шукають корені, які в даному випадку не такі і прості.
А потрібно знайти їх добуток!
Слідкуйте завжди за умовою.
Приклад 3. Обчислити х+у, якщо вони є розв'язками системи показникових рівнянь
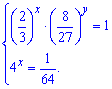
Розв'язання: Маємо систему показникових рівнянь з двома невідомими. Легкість обчислень полягає в тому, що з другого рівняння ми можемо знайти першу величину і підставити в 1 рівняння. Перетворимо 2 рівняння до стандартного виду
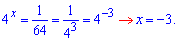
Одна змінна рівна x=-3. Підставимо її в перше рівняння
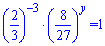
Звоседемо до тієї ж основи другу дужку
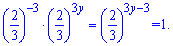
Щоб число в певному степені було рівне одиниці (що стоїть справа), необхідно, за властивістю показників, щоб степінь дорівнював нулю. Розв'язки рівняння легко отримати із наступної залежності
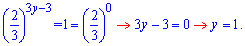
Згідно умови завдання, знаходимо суму розв'язків -3+1=-2.
Приклад 4. Знайти суму розв'язків рівняння
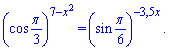
Розв'язання: В основі показникового рівняння маємо тригонометричні функції. Не важко здогадатися, що в подібних прикладах вони повинні приймати однакові за модулем значення або обернені (2 і 1/2 у випадку тангесів, котангенсів). Косинус 60 градусі рівний синусу 30 і =1/2.
Простими словами - основи рівні, залишилося прирівняти показники і розв'язати квадратне рівняння.
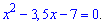
Знову є два варіанти:
1. Шукати корені через дискримінант і сумувати їх.
2. Застосувати теорему Вієте. За Вієтом сума коренів, взята з протилежним знаком відповідає значенню при змінній, тобто
x1+x2=-(-3,5)=3,5.
Це були приклади для розминки.
Складні показникові рівняння. Схеми зведення до простих
Приклад 5. Знайти більший розв'язок рівняння
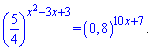
Розв'язання: Перепишемо праву сторону показникового рівняння
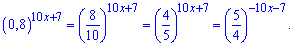
Тут ми піднесли до (-1) степеня основу, відповідно в показнику поміняли знак на протилежний. Прирівнюючи показники, отримаємо квадратне рівняння
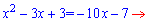
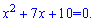
Корінь з дискримінанту рівний 3.
Більший корінь приймає значення х=(-7+3)/2=-2.
Правиьна відповідь знайдена. Складність в таких завданнях полягає, що частині школярів, як і студентів, зазвичай незрозуміло як таке рівняння привести до показникового.
Приклад 6. Знайти від'ємний розв'язок рівняння
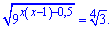
Розв'язання: В цьому прикладі потрібно звести обидві сторони показникового рівняння до однієї основи. Виконуємо перетворення
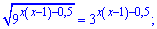
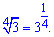
Остаточне рівняння таке

Основи тут рівні, прирівнюємо степені
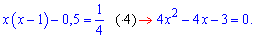
Знаходимо дискримінант квадратного рівняння та шуканий від'ємний розв'язок
x=(4-8)/(2*4)=-0,5.
Ось така тяганина з показниками може Вам підвернутися на тестуванні, тому будьте готові до всього.
Приклад 7. Знайти натуральний розв'язок рівняння
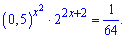 .
.
Розв'язання: Зводимо показникові рівняння до однієї основи
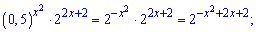
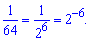
Рівняння спроститься до стандартного
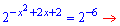
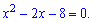
Обчислюємо дискримінант
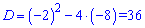
та корені рівняння
x1=(2+6)/2=4;
x2=(2-6)/2=-2 – не є натуральним числом.
Отже єдина правильна відповідь x=4.
Приклад 8. Скільки розв'язків має рівняння?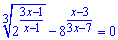
Розв'язання: Схема обчислень дещо мудрувата, але зрозуміла усім.
Переносимо один доданок за знак рівності і зводимо частини рівняння до спільної основи
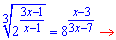
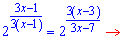
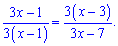
Показникові рівняння звели до дробового. Перш за все виписуємо обмеження на ОДЗ – виключаємо нулі знаменника
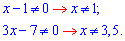
Переходимо до перехресного множення
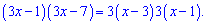
розкриваємо дужки і групуємо подібні доданки
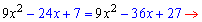
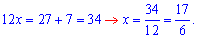
Отримали, що рівняння має один розв'язок. Ось і все на сьогодні, якщо Вам відповіді допомогли - ставте "лайк", ні - шукайте, що Вам потрібно.
На сайті безліч доступних роз'язків, які стануть на допомогу в підготовці до іспитів, можливо декому замінять репетитора. Надсилайте відсутні алгоритми обчислень, при нагоді рекомендуйте цікаві схеми одногрупникам та знайомим.


