Знання властивостей коренів та показникових функцій дає широкий набір інструментів для розкриття та спрощення ірраціональних виразів. Далі зібрані відповіді до понад 150 прикладів із ЗНО підготовки з математики, які охоплюють широкий клас шкільної програми зі спрощення та обчислення кореневих виразів, розв'язування ірраціональних рівнянь та нерівностей. Приклади добре розписані, тому можуть бути використані як інструкція чи методичка з розрахунку аналогічних завдань.
Завдання переважно підібрані від простих до складних, тому не розібравшись з простими ірраціональними виразимо просимо не починати розв'язувати рівняння чи нерівності. Це може мати непередбачувані наслідки в плані правильності обчислень та трактування відповідних формул.
Приклад 5.1 Обчислити: √6400+√49+√0,04+√0,0025
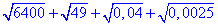
А | Б | В | Г | Д |
807,025 | 870,25 | 87,0205 | 87,25 | 870,025 |
Обчислення: Під коренями виділяємо повні квадрати, для цього в третьому та четвертому доданках числа представляємо у вигляді дробів, корені чисельника та знаменника яких легко визначити. Перші два корені рівні 80 та 7 відповідно
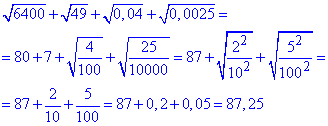
Далі від дробів повертаємося до десяткових записів чисел та підсумовуємо результат.
Отримаємо 87,25, що відповідає варіанту Г тестів.
Відповідь: 87,25 – Г.
Приклад 5.2 Обчислити вираз:
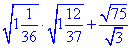

Обчислення: Для спрощення добутку коренів цілі частини вносимо під дріб.
В другому доданку дріб коренів розписуємо як корінь з дробу, оскільки показники однакові.
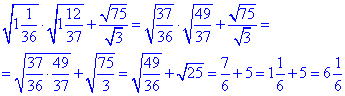
Після спрощень на однакові множники позбуваємося кореня квадратного шляхом виділення квадрату в першому доданку 49/36=72/62 та виконуємо сумування. В результаті прийдемо до значення, що відповідає варіанту Д тестових завдань.
Відповідь: 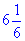 – Д.
– Д.
Приклад 5.3 Знайти значення виразу 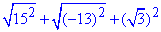
А | Б | В | Г | Д |
5 | 31 | 37 | 32 | 42 |
Обчислення: В даному прикладі потрібно вирази що містяться під коренем в квадраті взяти за модулем
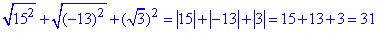
В результаті сума коренів квадратних рівна 31.
Відповідь: 31 – Б.
Приклад 5.4 Спростити вираз 10√2+√8+√50.
А | Б | В | Г | Д |
17√2 | 39√2 | 37√2 | 19√2 | 24√2 |
Обчислення: На перший погляд важке завдання, оскільки під коренем маємо радикали різних чисел.
Але після детального аналізу можна зауважити, що двійку під коренем можна виділити в кожному доданку. Все що залишиться можна записати через квадрати чисел і винести з під кореня.
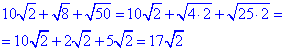
Після сумування отримаємо значення 17√2, що відповідає варіанту А тестів.
Відповідь: 17√2 – А.
Приклад 5.5 Знайти значення виразу 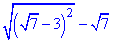
А | Б | В | Г | Д |
17√2. | 39√2 | 37√2 | 19√2 | 24√2 |
Обчислення:Студенти та учні часто роблять помилки в подібного роду прикладах, а все тому що думають, що якщо під коренем мають квадрат виразу то при розкритті отримаємо сам вираз. Проте це неправильно, слід брати вираз за модулем, а для цього слід оцінити значення виразу.
Аналізуючи вираз в дужках під коренем приходимо висновку:
√7<3, оскільки 7<9, тому √7-3<0,
що він приймає від'ємне значення, тому при розкритті модуля його беремо з протилежним знаком 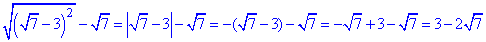
Завжди пам'ятайте це правило!
Відповідь: 3-2√7 – Б.
Приклад 5.6 Обчислити значення виразу: 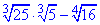
А | Б | В | Г | Д |
1 | 2 | 3 | 4 | 5 |
Обчислення: Маємо різницю коренів, перший доданок містить добуток кубічних коренів тому тут слід виділити куб числа.
Другий доданок містить корінь 4-го порядку, але легко здогадатися, яке число в четвертій степені рівне 16.
В результаті розкриття коренів отримаємо значення, яке рівне 3.
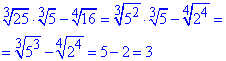
Відповідь: 3 – В.
Приклад 5.7 Вказати правильну рівність.
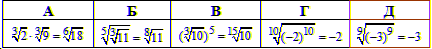
Обчислення:Подібні тестові завдання добре показують, хто вчив теорію, а хто ні.
Також важливо знати властивості показників, а саме коли їх сумуємо, а коли множимо.
Як це виглядає на практиці добре ілюструють пояснення до завдання, що виражені наступними формулами.
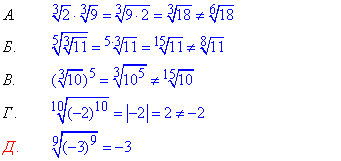
Таким чином приходимо до того, що лише одне з наведених в тестах тверджень є правильним.
Відповідь: 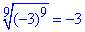 – Д.
– Д.
Приклад 5.8 Обчислити 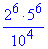
А | Б | В | Г | Д |
101,5 | 102 | 108 | 109 | 1010 |
Обчислення: Враховуючи властивості показникових функцій, спрощуємо чисельник дробу, а далі сам дріб
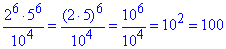
Відповідь: 102 – Б.
Приклад 5.8a Обчислити: 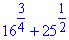 .
.
А | Б | В | Г | Д |
9 | 12 | 13 | 15 | 31 |
Обчислення: Для розкриття ірраціональності запишемо 16 як 2 в 4 степені, а 25 як 5 в квадраті та спростимо за формулою
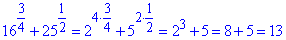
Результат відповідає варіанту В тестів.
Відповідь: 13 – В.
Приклад 5.9 Обчислити вираз: 9^(3/2)+64^(-1/3)
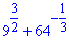
А | Б | В | Г | Д |
27,25 | 31 | 278 | 27 | -7 і 5/6 |
Обчислення: По аналогії з попереднім завданням позбуваємося ірраціональності в доданках та знаходимо їх суму
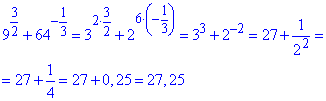
Відповідь: 27,25 – А.
Приклад 5.10 Знайти значення виразу:

А | Б | В | Г | Д |
200 | 8000 | 1600 | 400 | 800 |
Обчислення: Корінь кубічний записуємо через показник (1/3), далі за властивостю показників множимо 1/3 на показник кожного з підкореневих множників. В результаті отримаємо:
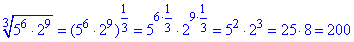
Відповідь: 200 – А.
В наступних уроках розберемо більше 30 прикладів на розкриття ірраціональності, а далі перейдемо до розв'язування ірраціональних рвнянь та нервностей.


