До ірраціональних належать рівняння в яких вираз зі змінною чи сама змінна міститься під знаком кореня або дробового степеня. При розв'язуванні рівнянь в першу чергу встановлюють обмеження на область визначення (ОДЗ). Далі є кілька способів розкриття ірраціональності, основні з них це піднесення до степеня та заміна змінної. При парних степенях коренів часто виникають зайві розв'язки, тому після обчислень методом підстановки слід перевірити чи всі знайдені значення перетворюють початкове рівняння в тотожність.
Далі будуть дані відповіді до понад 50 прикладів із ЗНО підготовки на ірраціональні рівняння, перегляньте їх та вивчіть алгоритми знаходження розв'язків.
Приклад 12.1 Знайти область визначення (область допустимих значень) рівняння
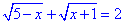
А | Б | В | Г | Д |
R | x∈(-∞;-1] | x∈[5;+ ∞) | (-1;5) | [-1;5] |
Обчислення: Перші завдання досить прості, і нам всього навсього потрібно з обмежень на кореневі функції встановити нерівності, з яких отримаємо ОДЗ:
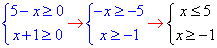
Далі можемо побудувати числову вісь і на ній зобразити ОДЗ

Часто учителі та викладачі вимагають будувати графічно області, тому ми їх для простих завдань будемо наводити.
З обмежень на корені встановили, що областю визначення є проміжок x∈[-1;5], що відповідає варіанту Д ЗНО тестів.
Відповідь: [-1;5] – Д.
Приклад 12.2 Вказати рівняння, областю визначення якого є одне число.
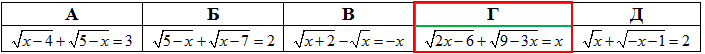
Обчислення: Маємо 5 ірраціональних рівнянь, кожне з яких містить суму або різницю двох коренів квадратних зі змінними. Для кожної умови складаємо систему із двох нестрогих нерівностей
А. 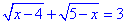
Записуємо ОДЗ:
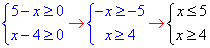
Відкладаємо область визначення на числовій осі
 та у вигляді проміжку xє[4;5].
та у вигляді проміжку xє[4;5].
Далі переходимо до наступного пункту
Б. 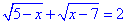
Система нерівностей для ОДЗ:
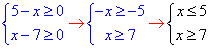
Будуємо графік області визначення 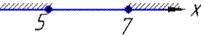 Оскільки інтервали не перетинаються, x∈∅, то ОДЗ є порожня множина, тобто рівняння немає розв'язків.
Оскільки інтервали не перетинаються, x∈∅, то ОДЗ є порожня множина, тобто рівняння немає розв'язків.
Перевіряємо наступне рівняння.
В. 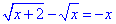
Виписуємо ОДЗ:
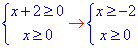
Можемо зразу записати область визначення x∈[0;+ ∞), а можна ще добавити графік ОДЗ на числовій осі
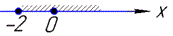
Залишилось перевірити ще 2 рівняння з коренями
Г. 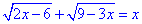
Встановлюємо ОДЗ:
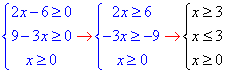
На числовій осі отримаємо лише одну точку
 Отже, xє{3}, або x=3.
Отже, xє{3}, або x=3.
Розпишемо останнє рівняння
Д. 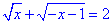
ОДЗ: 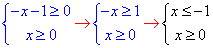
Оскільки розв'язок одночасно не може бути більший рівний нулю і менший рівний мінус одиниці
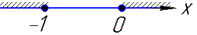 то областю визначення є порожня множина x∈∅.
то областю визначення є порожня множина x∈∅.
Відповідь: 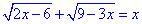 – Г.
– Г.
Приклад 12.3 Вказати рівняння, область визначення якого є порожня множина.
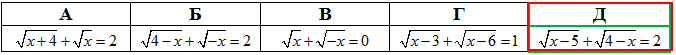
Обчислення: В попередньому завданні мали два рівняння що мали областю визначення порожні множини.
Перевіримо наведені ірраціональні рівняння і з'ясуємо, яке ж з них точно немає розв'язків.
А. 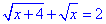
З обмежень на корені виписуємо систему нерівностей для визначення області визначення:
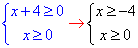
Після спрощень наносимо точки та заштриховуємо ОДЗ на числовій осі
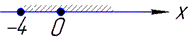 Отже, x∈[0;+ ∞).
Отже, x∈[0;+ ∞).
Б. 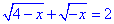
Виписуємо обмеження кореневих функцій:
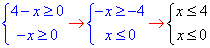
На числовій осі спільним інтервалом
 із двох нерівностей буде наступний x∈(-∞;4].
із двох нерівностей буде наступний x∈(-∞;4].
В. 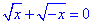
Система нерівностей для області визначення:
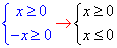
 Звідси xє{0}, або x=0.
Звідси xє{0}, або x=0.
Г. Для ірраціонального рівняння
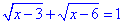
виписуємо ОДЗ:
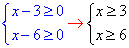
Заштриховуємо області на числовій осі та переконуємося, що їх перетином
 є інтервал x∈[6;+ ∞).
є інтервал x∈[6;+ ∞).
Д. Залишилось останнє для перевірки рівняння
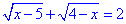
Виписуємо систему нерівностей з ОДЗ коренів:
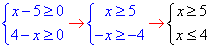
Корені снують при змінних не більших за 4 і не менших за 5, звідси робимо висновок,
 що областю визначення є порожня множина x∈∅, що й треба було встановити в умові прикладу.
що областю визначення є порожня множина x∈∅, що й треба було встановити в умові прикладу.
Відповідь: 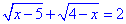 – Д.
– Д.
Приклад 12.4 Вказати рівняння, коренем якого є число 2.

Обчислення: В таблиці ЗНО тестів ми вже виділили правильну відповідь до завдання, але щоб її отримати довелося розв'язати 5 ірраціональних рівнянь.
І пам'ятайте, що коли права частина рівна нулю і маємо аналогічні приклади то слід відсіяти ті корені, що не задовільняють ОДЗ, або принаймні перевірити їх методом підстановки.
Ми ж покажемо повний хід аналізу рівнянь.
А. 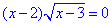
ОДЗ: x-3≥0, звідси x≥3.
В інтервальній формі ОДЗ має запис x∈[3;+ ∞).
Кожний з множників прирівнюємо до нуля та розв'язуємо рівняння
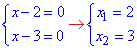
але x1=2 не належить ОДЗ, тому x=3.
Можете переконатися, що при підстановці x=2 отримаємо корінь квадратний з від'ємного числа.
Б.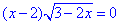
ОДЗ: 3-2x≥0, -2x≥-3, звідси x≤1,5.
Остаточно x∈(- ∞; 1,5].
Розв'язуємо рівняння
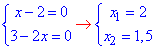
але один з коренів x1=2 не належить ОДЗ, тому x=1,5.
В. 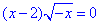
Підкоренева функція повинна приймати невід'ємні значення, тому нерівність для ОДЗ має вигляд:
-x ≥0, звідси x≤0.
У вигляді півінтервалу це рівносильне x∈(- ∞;0].
Знаходимо корені рівняння
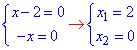
Їх кількість рівна двом, але x1=2 не належить ОДЗ, тому єдиний правильний розв'язок x=0.
Г. Для рівняння 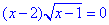
складаємо ОДЗ: x-1≥0, звідси x≥1.
Отже, x∈[1;+∞).
Обчислюємо корені
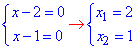
Бачимо, щообидва корені належать ОДЗ.
Отже, x=2 є коренем рівняння, початкова умова виконана.
Д. Для себе можемо перевірити останнє рівняння
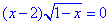
Область визначення встановлюємо з нерівності:
1-x≥0, -x≥-1, звідси x≤1.
ОДЗ x∈(- ∞;1].
Знаходимо корені
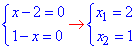
Перший знайдений x1=2 не належить ОДЗ, тому залишається x=1.
Відповідь: 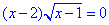 – Г.
– Г.
Попереду ще понад 40 прикладів на ірраціональні рівняння.
Переходьте та аналізуйте готові відповіді із ЗНО тестів.


