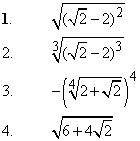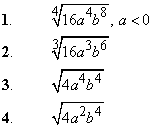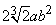Щоб добре розібратися в схемах розкриття коренів, виділення повних квадратів, роботі з показниками розглянемо наступні відповіді із серії 50 прикладів на ірраціональні вирази. Якщо завдання для Вас надто складні, а обчислення незрозумілі, то спробуйте повернутися до попередніх уроків та переглянути простіші приклади.
Приклад 5.21 Обчислити вираз:
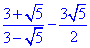
Обчислення: Спершу зведемо дроби до спільного знаменника.
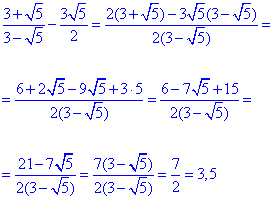
В цьому прикладі отримали пропорційний до знаменника ірраціональний вираз в чисельнику.
На практиці можливі складніші випадки, коли спростити не вдається. Тоді для правильності представлення відповіді слід помножити та поділити дріб на спряжений до знаменника вираз та позбутися в знаменнику ірраціональності. Пам'ятайте про це!
Відповідь: 3,5 – Г.
Приклад 5.22 Знайти значення виразу 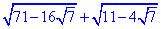 .
.
А | Б | В | Г | Д |
1 | 2 | 3 | 4 | 5 |
Обчислення: На перший погляд виглядає що тут немає вже куди спрощувати, але це не так. На попередніх уроках ми розбирали, що у випадках коли маємо вложені корені слід виділити повні квадрати та позбутися зовнішніх коренів. При цьому не забуваємо, що при парних степенях коренів при розкритті беремо не сам вираз, а його значення за модулем.
На практиці все оформляємо як у формулі далі
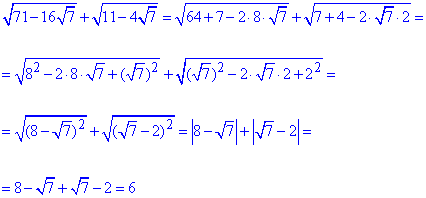
Зверніть увагу, що від правильності розкриття модулю багато залежить, тому якщо маєте сумніви, то спершу оцініть який з доданків під модулем більший.
Відповідь: 6 – Д.
Приклад 5.23 Обчислити:
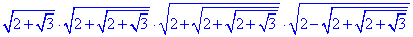
А | Б | В | Г | Д |
1 | 2 | 3 | 4 | 5 |
Обчислення: З таблиці бачимо, що при спрощенні добутку триповерхових коренів прийдемо до простого числа.
Спробуйте розв'язати приклад самостійно, а далі порівняти хід розрахунків з наведеним далі.
Алгоритм полягає в тому, що з кінця і до початку слід зводити добутки коренів під формулу різниці квадратів. Тут вона тричі була застосована, щоб вкінці отримати одиницю.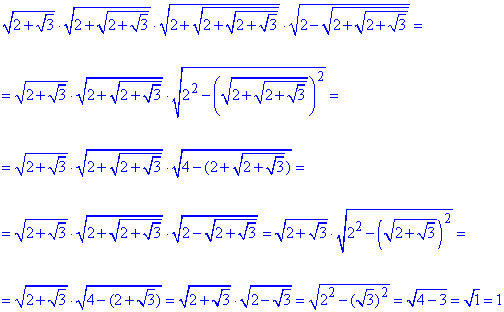
Надіюсь у нас з вами відповіді однакові.
Формула розбита на багато рядків для зручності перегляду з мобільних, з розвитком технологій все більше студентів та учнів мають доступ до навчальних матеріалів на подобі нашого ресурсу. Фільтруйте для себе якісні ресурси та додавайте їх в закладки, діліться з друзями.
Відповідь: 1 – А.
Приклад 5.24 Обчислити: 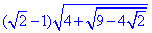
А | Б | В | Г | Д |
1 | 2 | 3 | 4 | 2√2 |
Обчислення: Завдання на розкриття ірраціональності ускладнюються, і черговий приклад є тому тільки доказом.
З аналізу таблиці бачимо, що відповідь може бути простим числом, а для цього три вкладені корені мають дати вираз спряжений до (√2-1).
Для цього слід побачити повний квадрат під другим коренем, що не є очевидним для початківців.
В результаті розкриваємо внутрішній корінь і за тією ж схемою виділяємо повний квадрат в зовнішньому корені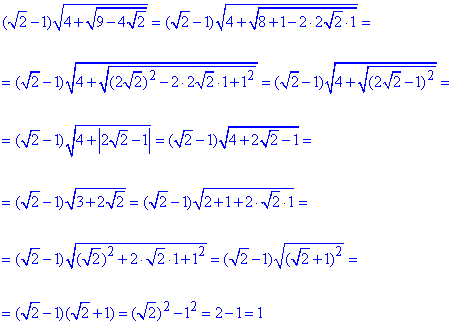
Далі приходимо до різниці квадратів, яку Вам не вперше розкривати.
Уважно перегляньте хід розрахунків та запам'ятайте, що якщо немає ідей як спрощувати вложені корені то скоріш за все перед вами спрощений квадрат якогось виразу. Виділяючи частину з коренем як подвоєний добуток доданків поступово приходимо до квадрата виразу, що містить корінь.
Цього не так просто навчитися, але постійна практика та самостійна робота над собою роблять подібні завдання цікавими та легкими.
Відповідь: 1 – А.
Приклад 5.25 Обчислити:
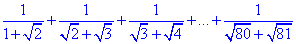
А | Б | В | Г | Д |
1 | 3 | 5 | 8 | 9 |
Обчислення: Задано суму 80 членів ряду, що містить ірраціональність в знаменнику. Для обчислень подібних прикладів спершу слід позбутися ірраціональності в знаменнику, для цього домножуємо на дріб де в чисельнику і знаменнику маємо вираз спряжений до знаменника. Далі шукаємо закономірності, які дозволяють згрупувати подібні доданки та знайти суму ряду
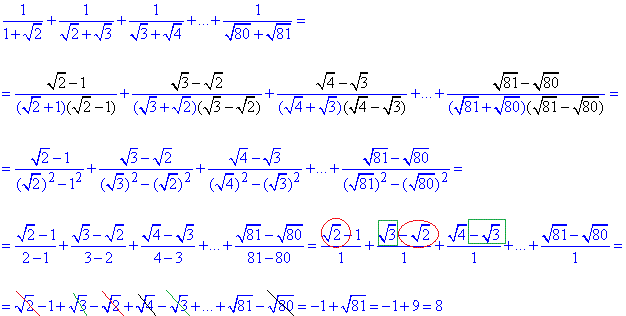
Запам'ятайте цю методику і використовуйте всюди де маєте ряди з ірраціональністю в знаменнику.
Отримали варіант Г із ЗНО тестів.
Відповідь: 8 – Г.
Приклад 5.26 Установити відповідність між заданими виразами (1–4) та виразами, які їм тотожно дорівнюють (А – Д).
| А. 2+√2 |
Обчислення: Використовуємо правило, згідно з яким корінь парного степеня з виразу в парному тому ж степені рівний виразу взятому за модулем. Для непарних степенів кореня при розкритті отримаємо сам вираз.
В результаті для чотирьох варіантів отримаємо так відповіді:
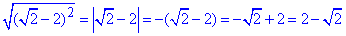 , 1 - В.
, 1 - В.
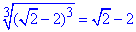 , 2 - Д.
, 2 - Д.
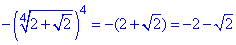 , 3 - Б.
, 3 - Б.
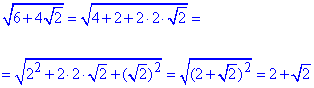 , 4 - А.
, 4 - А.
На ЗНО тестах з математики правильною буде відповідь 1- В, 2 - Д, 3 - Б, 4 - А.
Приклад 5.27 Установити відповідність між заданими виразами (1–4) та виразами, які їм тотожно дорівнюють (А – Д).
| А. 2|a|b2 |
Обчислення: Для розкриття ірраціональності врахуємо що a<0, та внесемо число під модуль.
В результаті прийдемо до наступного результату
1)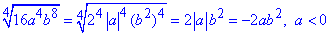 - В.
- В.
2) Якщо степінь кореня непарний, то числа під коренем можуть бути від'ємними
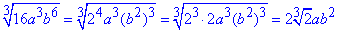 - Д.
- Д.
Це напряму слідує з ОДЗ кореневих функцій
3) В окремих випадках немає значення знак числа, зазвичай, тоді після розкриття коренів маємо квадрат чи парний степінь від'ємного виразу
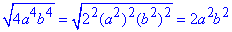 - Б.
- Б.
4) В останньому завданні ірраціональність розкриваємо по аналогії з першим завданням
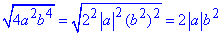 - А.
- А.
Приклад 5.28 Установити відповідність між виразами (1–4) та їх значеннями (А – Д).
1. (-27)1/3 | А. -1/3 |
Обчислення: Враховуючи властивості показникових функцій, перетворюємо задані вирази
1) 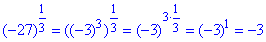 - В.
- В.
2)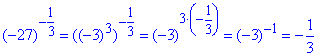 - А.
- А.
3) 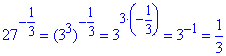 - Б.
- Б.
4) 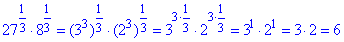 - Д.
- Д.
З формул Ви можете поступово розібратися з прийомами, які слід застосовувати в тому чи іншому випадку.
Попереду ще кільканадцять прикладів на спрощення ірраціональних виразів. Якщо розібралися з наведеними відповідями, то можете переходити до вивчення наступних схем розкриття ірраціональностей.