Основні методи розкриття ірраціональності вивчають в шкільній програмі. З їх допомогою можна розв'язати безліч ірраціональних рівнянь та нерівностей. Важливою особливістю обчислень ірраціональних рівнянь є необхідність перевіряти корені на правильність. Через це і виникає велика кількість помилок та неправильних рішень на контрольних, тестах, олімпіадах. Нижче наведені поширені ірраціональні рівняння, поширені помилки при їх обчисленні та самі методи розкриття ірраціональності.
Приклад 1. Розв'язання рівняння 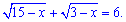
Розв'язання. Сума коренів рівна додатному числу, це означає, що хоча би один з коренів не нульовий. Область допустимих значень (ОДЗ) спільна для двох функцій наступна
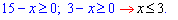
Перебиранням можливих значень можна отримати, що x=-1 є розв'язком ірраціонального рівняння. Однак наша мета навчитися розв'язувати рівняння, а не вгадувати корені. Тому, для зручності переносимо любий корінь за знак рівності і підносимо до квадрату
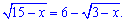
Це потрібно для зменшення складності обчислень. Щоб переконатися, спробуйте піднести до квадрату обидві сторони початкового рівняння і довести обчислення до кінця.
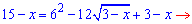
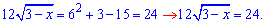
Ділимо на 12 і знову підносимо до квадрату
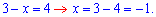
Отримали потрібний розв'язок за всіма правилами розкриття ірраціональностей. Крім цього він задовольняє ОДЗ.
Приклад 2. Розв'язання рівняння 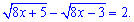
Розв'язання. Тут бачимо, що змінні при піднесенні до квадрату зануляться. Переносимо корінь з мінусом за знак рівності і підносимо до квадрату
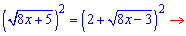
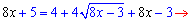
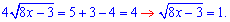
Повторно підносимо до квадрату, щоб позбутися кореня
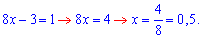
Підстановкою у корені переконуємося, що x=0,5 є розв'язком ірраціонального рівняння
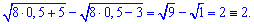
Приклад 3. Визначити середнє арифметичне розв'язків рівняння 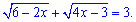
Розв'язання. Дане ірраціональне рівняння потрібно детально аналізувати. Знайдемо ОДЗ кореневих функцій
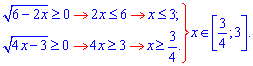
Саме з цього проміжку розв'язки нас цікавлять. Переходимо до розкриття ірраціональності

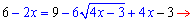
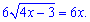
Ділимо на 6 і підносимо обидві сторони рівняння до квадрату
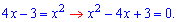
В такий спосіб вдалось звести ірраціональне рівняння до квадратного. Корені останнього дає Теорема Вієта
x=3; x=-1.
Так як ми обмежили розв'язок через ОДЗ, то єдиним вірним значенням є x=3. Якщо неможливо обмежити ОДЗ, то слід виконати перевірку. Без перевірки при піднесенні до квадрату і розкритті ірраціональності часто виникають зайві корені.
На практиці за цим постійно треба слідкувати і перевіряти знайдені значення підстановкою.
Приклад 4. Визначити менший корінь рівняння 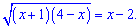
Розв'язання. Маємо просте ірраціональне рівняння, корені якого можна перевірити в кінці. Виконаємо розкриття ірраціональності піднесенням до квадрату
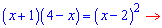
Розкриваємо дужки і групуємо подібні доданки
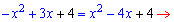
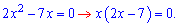
Корені рівні x=0 і x=7/2=3,5.
І тут багато хто впише 0 у відповідь, оскільки нуль менше із двох значень.
А про перевірку всі забули!
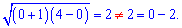
Виходить, що 0 не є коренем.
А друге значення x=3,5
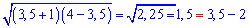
є шуканою відповіддю ірраціонального рівняння.
Приклад 5. Визначити більший корінь рівняння 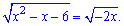
Розв'язання. Якщо не аналізувати ірраціональні рівняння, то можна припуститися багатьох помилок. Наприклад, з другого кореня бачимо, що нас цікавлять від'ємні значення, оскільки при x< 0 підкоренева функція додатна. Підносимо корені до квадрату
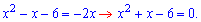
За теоремою Вієта корені квадратного рівняння рівні x=-3; x=2.
x=2 ми вже викреслили з коренів, згідно з ОДЗ. (хоча 2>-3). Отже, більшим коренем ірраціонального рівняння є x=-3. Без підстановки або аналізу ОДЗ могли отримати невірне значення, а на контрольній чи тестах – недораховані бали.
Висновки робіть самі!
Приклад 6. Розв'язання рівняння 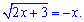
Розв'язання. Частина абітурієнтів, якщо це тести зразу кинулася шукати корені. Аналізувати ніхто не любить, а часом – і не вміє. Зліва маємо корінь, тобто додатне значення. Справа змінна з від'ємним знаком. Щоб таке мало місце, необхідно, щоб змінна була від'ємною. Враховуючи вище сказане корінь ірраціонального рівняння має належати інтервалу
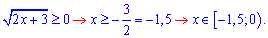
Причому цей корінь єдиний. Підстановкою першого цілого значення x=-1 одразу ж отримаємо рівність
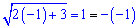
тобто без розкриття ірраціональності знайшли корінь рівняння x=-1.
Приклад 7. Розв'язання рівняння 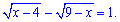
Розв'язання. Знайдемо область допустимих значень коренів
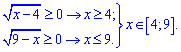
Отже корінь належить проміжку [4;9]. Підстановкою значень можна отримати, що при x=8 ірраціональне рівняння виконується
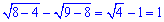
таким чином, методом виключення у швидкий спосіб знайшли потрібне значення.
Приклад 8. Скільки коренів має рівняння 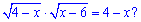
Розв'язання. Запишемо область значень кореневих функцій
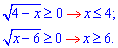
Отримали два інтервали, які не мають точок перетину, тобто рівняння немає розв'язків. Якщо б не визначати ОДЗ, то ми б підносили до квадрату, далі визначали корені. Дехто, можливо, порахував би їх кількість. Інші б підстановкою переконалися, що отримані значення не є розв'язками. В кожному з випадків Ви потратите чимало часу, які часом надто дорогі при контрольній, вступі, тестуваннях. Тому для себе постановіть за правило, де просте ірраціональне рівняння – там виписуєте ОДЗ, складніше завдання – робите перевірку!
Переглянути схожі матеріали:


