Продовжуємо вивчати, як правильно позбуватися ірраціональності та спрощувати такі вирази. Завдання, що далі розв'язані взяті із програми підготовки до ЗНО тестування, тому Ви добре знаєте де їх можете використати. Методи та схеми, що тут будуть наведені є загальновідомими, систематизованими та без вагань можуть бути застосовані Вами до аналогічних прикладів на ірраціональні вирази. Уважно розбирайте відповіді та вчіться красиво оформляти розв'язки.
Приклад 5.11 Звільнитися від ірраціональності в знаменнику дробу  .
.
Обчислення:В цьому і всіх подібних прикладах для розкриття ірраціональності в знаменнику слід домножити і поділити дріб на вираз спряжений до знаменника. За формулою різниці квадратів в знаменнику дістанемо різницю чисел.
Для цього завдання рівносильні перетворення наведені формулою
Бувають складніші приклади, коли для розкриття ірраціональності слід звести знаменник під різницю кубів, але про них піде мова пізніше.
Ми в свою чергу стараємося подавати матеріал від простого до складнішого, щоб Ви все засвоїли з першого разу.
Відповідь: (√7+1)/2 – А.
Приклад 5.12 Внести множники під знаки коренів: a√(-a)+b√b.
ОДЗ: a≤0; b≥0.
Обчислення: Уважно переглянь те переходи в обчисленнях. Перевірте, чи самостійно Ви могли б прийти до наведеної відповіді
Вона в нас точно правильна, тому добре запам'ятайте як вносити від'ємні значення під корінь квадратний.
Відповідь:  – Д.
– Д.
Приклад 5.13 Спростити ірраціональний вираз

Обчислення: Переходимо до завдань на вкладені корені.
Вони вимагають добрих знань показникових функцій та послідовного розкриття коренів від внутрішнього вложеного до головного над усіма.
Скористаємося правилами та спростимо вираз 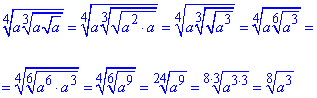
(при a≥0).
Уважно розберіть це завдання, далі підуть тільки важчі умови.
Відповідь:  – Г.
– Г.
Приклад 5.14Спростити вираз 
А | Б | В | Г | Д |
-a2b | -ab | a2b | a2b2 | ab2 |
Обчислення:Пригадуємо властивості показників та розписуємо вложені корені, аж поки не прийдемо до компактної відповіді .
.
Відповідь: a2b – В.
Приклад 5.15 Спростити вираз  .
.

Обчислення: По аналогії з попереднім завданням позбуваємося кореня кубічного від частки добутків показникових виразів.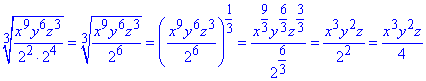
Після нескладних перетворень прийдемо до формули x3y2z/4, яка відповідає варіанту В тестових завдань.
Відповідь:x3y2z/4 – В.
Приклад 5.16 Знайти x, якщо 
А | Б | В | Г | Д |
-1,125 | -0,875 | -0,625 | -0,375 | -0,125 |
Обчислення: Спочатку спростимо вложені корені, що стоять у лівій частині рівняння: 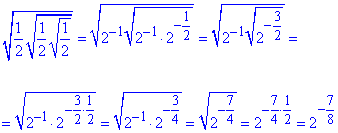
Прирівнюючи до правої частини, знаходимо невідоме значення:
 , тобто x=-7/8, x=-0,875.
, тобто x=-7/8, x=-0,875.
Відповідь: -0,875 – Б.
Приклад 5.17 Спростити вираз 
А | Б | В | Г | Д |
0 | 4 | -4 | 4+2√5 | 2√5 |
Обчислення: При розкритті коренів від квадратів виразів отримаємо вирази за модулем. Далі оцінюємо чи підмодульний вираз додатний чи від'ємний. Якщо додатний то просто опускаємо модульні дужки, якщо приймає від'ємне значення то при розкритті модуля міняємо знак на протилежний.
Для наведеного прикладу відповідь можна сформулювати в наступному вигляді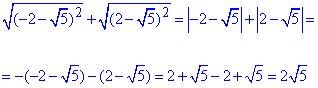
Відповідь: 2√5 – Д.
Приклад 5.18 Знайти значення виразу  , якщо x=√10.
, якщо x=√10.
А | Б | В | Г | Д |
-4,5 | 2√10-10,5 | 2x-10,5 | 4,5 | 3,5 |
Обчислення: Мамо суму коренів четвертого порядку від виразу в у 4 степені. Для розкриття коренів поступаємо як і у попередньому прикладі, записуємо модулі таі після аналізу підмодульних виразів записуємо кінцеві значення.
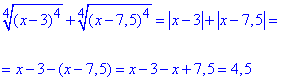
тут мали x-3=√10-3>0 і x-7,5=√10-7,5<0
Чим більше Ви самостійно розв'яжете ідентичних за змістом прикладів, тим краще Вам запам'ятаються правила розкриття коренів та модулів.
Одних переглядів готових відповідей до ірраціональних виразів замало, щоб швидко обчислювати такі приклади самостійно, тому практикуйте побільше і почастіше.
Відповідь: 4,5 – Г.
Приклад 5.19Спростити вираз 
А | Б | В | Г | Д |
√10 | 3,5+√10 | √3+2 | √2+√5 | 1+√6 |
Обчислення:Якщо маєте два вкладених корені і не бачите явної схеми як їх спростити то спробуйте розписати підкореневий вираз та подати його у вигляді квадрату виразу, що містить ірраціональність. Спершу Вам це буде важко вдаватися, але далі все легше зможете працювати з коренями.
В цьому завданні корінь з 10 розпишемо як корінь з 2 помножити на 5, а далі перегрупуємо доданки так як у випадку суми коренів з 2 та 5 в квадраті.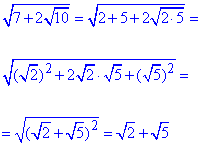
Запам'ятайте цю схему розкриття коренів, вона вимагає уваги до деталей та деякої практики.
Відповідь: √2+√5 – Г.
Приклад 5.20 Звільнитись від ірраціональності в знаменнику дробу 
Обчислення: В знаменнику маємо різницю коренів кубічних з 7 та 2. Щоб позбутися ірраціональності в знаменнику необхідно отримати формулу різниці кубів, а для цього весь дріб необхідно розділити та помножити на вираз, що це забезпечує.
За формулою різниці кубів записуємо відповідний множник та виконуємо перетворення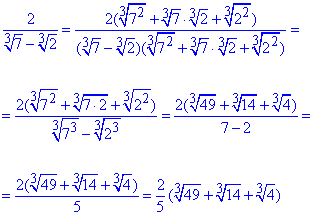
Формули різниці кубів та квадратів варто мати під рукою, щоб не наробити помилок в подібних завданнях та прийти до правильного результату.
Відповідь:  – В.
– В.
Далі підуть складніші в плані обчислень приклади із розкриття ірраціональності та знаходження значення ірраціонального виразу. Уважно перегляньте наведені завдання та вивчіть схему зведення під формулу квадрату виразу. Наступні 20 прикладів із ЗНО підготовки будуть розв'язані в наступних трьох публікаціях.
Після цього перейдемо до ірраціональних рівнянь та нерівностей.


