Ірраціональними називають рівняння, в яких невідома величина розміщена під знаком кореня певного степені. Найпростіші ірраціональні рівняння розв'язуються або піднесенням до степеня, або заміною. Складніші ірраціональні рівняння зводяться до попередніх деякими штучними методами. Наприклад, таке на перший погляд складне рівняння
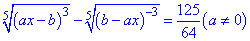
зводиться до квадратного заміною
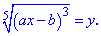
Часто при розкриті ірраціональності використовують формулу складного радикала
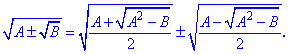
Варто зазначити, що при розв'язуванні ірраціональних рівнянь необхідно визначати область допустимих значень. Крім того, варто робити перевірку, підставляючи знайдені значення невідомих у вихідне рівняння, оскільки при піднесенні до степеня ми збільшуємо степінь рівняння, що може привести до появи сторонніх коренів.
Прості ірраціонаьні рівняння
Приклад1. Знайти розв'язок рівняння
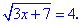
Розв'язання:Знаходимо область допустимих значень
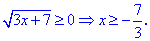
Підносимо обидві частини рівняння до квадрату та розв'язуємо
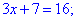
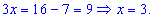
Отримали один розв'язок x=3.
Приклад 2. Знайти розв'язок рівняння
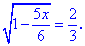
Розв'язання:ОДЗ для рівняння заходимо з нерівності
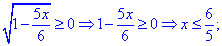
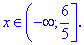
Розкриваємо ірраціональність рівняння та знаходимо корінь
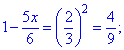
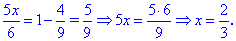
Він належить області допустимих значень, тобто – є розв'язком.
Приклад 3. Розв'язати рівняння
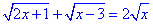
Розв'язання:Знаходимо область допустимих значень
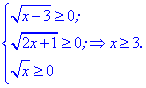
ОДЗ: 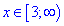
За описаною схемою підносимо обидві частини до квадрату, щоб позбутися ірраціональності.
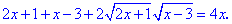
Переносимо всі доданки, крім коренів, в праву частину та спрощуємо
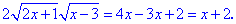
Для розкриття ірраціональності знову виконуємо піднесення до квадрату та спрощення
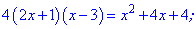
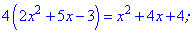
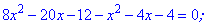
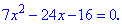
Отримали квадратне рівняння, корені якого знаходимо з допомогою дискримінанта
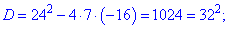
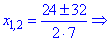
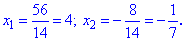
Другий корінь не належить області допустимих значень. Цю перевірку потрібно виконувати завжди, інакше отримаєте більше коренів ніж потрібно, причому вони не задовільнятимуть вихідне рівняння.
Отже, розв'язком буде одне значення x=4.
Ірраціонаьні рівняння середньої складності
Приклад 4. Розв'язати рівняння
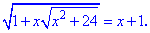
Розв'язання: Область допустимих значень для даного рівняння в простий спосіб знайти не вдасться, тому виконаємо розв'язання, після чого перевіримо підстановкою отримані корені.
Підносимо обидві частини рівняння до квадрату
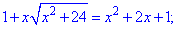
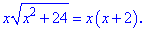
Даний вираз більшість з Вас спростила би на x та підносила до квадрату. Але це було б неправильно.
На x ділити можна коли він приймає ненульове значення. В даному випадку x=0 буде розв'язком рівняння, в чому легко перконатися
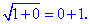
Після того, як ми це врахували можна продовжувати обчислення
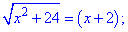
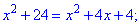
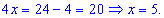
Виконуємо перевірку
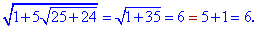
Отримали два корені рівняння x=0, x=6.
Приклад 5. Знайти розв'язок рівняння
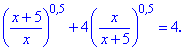
Розв'язання: Підносити до квадрату обидві сторони в подібних рівняннях не потрібно. Для спрощення робимо заміну
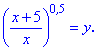
Рівняння перетвориться на наступне
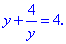
Множимо на змінну y і переписуємо у вигляді квадратного рівняння
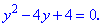
Теорема Вієта дає нам два однакові корені
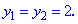
Повертаємося до заміни та знаходимо розв'язок
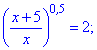
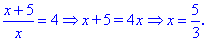
Значення x=5/3 задовільняє рівняння.
Приклад 6. Знайти розв'язок ірраціонального рівняння
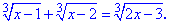
Розв'язання: Хочете чи ні, а такі приади обчислюють піднесенням до кубу обидвох сторін, тому пригадуємо формуи скороченого множення та знаходимо
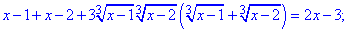
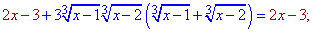
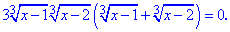
Варто зазначити, що вираз у дужках відповідає правій стороні заданного рівняння. В подібних прикладах такі ситуації зустрічаються часто, тому будьте уважними при розв'язанні. Робимо підстановку
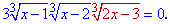
Прирівнюємо кожен з множників до нуля, та розв'язуємо
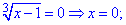
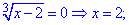
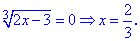
Перевірку спробуйте виконати самостійно. Вона покаже, що всі три знайдені значення перетворюють рівняння в тотожність.
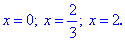
Остання частина легка і зрозуміла багатьом, проблемою залишається побачити, що доданки у третьому рядку рівні правій стороні рівняння. Ящо цього не робити, то доведеться обчилювати хоч і не складне, проте ще одне ірраціональне рівняння.
Приклад 7. Знайти розв'язок ірраціонального рівняння
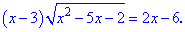
Розв'язання: Такий тип рівнянь придуманий для неуважних студентів. При спокійному аналізі можна побачити наступну закономірність

Стандартне піднесення до квадрату в даному випадку було довшим і складнішим шляхом до відшукання розв'язків. Із дужок отримаємо значення
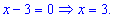
Спрощуємо вихідне рівняння та підносимо до квадрату
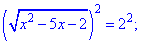
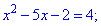
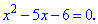
До отриманого квадратного рівняння обчислюємо дискримінант
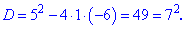
Корені рівняння знаходимо за формулою
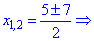
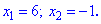
Таким чином встановлено, що подібні рівняння можуть мати до трьох розв'язків
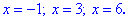
Вивчайте по можливості різні математичні пакети, вони полегшують навчання. Зокрема, в Maple останнє завдання вирішується кількома рядками
> restart;
> eq:=(x-3)*sqrt(x^2-5*x-2)=2*x-6;
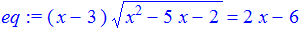
> solve({eq},{x});
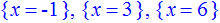
Просто і красиво. Проте і Maple може розв'язати далеко не всі ірраціональні рівняння, деякі корені не знаходить, в певних випадках підкореневі вирази потрібно довизначати. Однак для спрощення розрахунків є досить простою в плані коду програмою.
На цьому ознайомлення з ірраціональними рівняннями завершується. На практиці можна зустріти ірраціональні рівняння, які взагалі кажучи важко розв'язати наведеними методами, проте наближені корені знайти числово вдається. Тому, якщо у Вас при обчисленні виникнуть труднощі – звертайтеся, ми Вам допоможемо!
Переглянути схожі матеріали:


