Знайомство з прогресіями в шкільному навчанні розпочинається в 9, 10 класах з простих формул членів прогресій, знаменника прогресії, а вже тоді суми.
Послідовність (bn) називають геометричною прогресією (г/п), якщо кожен її наступний член більший або менший від попереднього в q раз
bn=bn-1q=b1qn-1.
Цей запис ще називають формулою n-го члена геометричної прогресії.
Темп зміни значень в такій послідовності q називають знаменником геометричної прогресії
q=bn/bn-1=bn+1/bn.
Якщо q<1 то маємо справу з нескінченно спадною геометричною прогресєю.
Формула суми геометричної прогресії для q>1
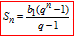
та суми нескінченно спадної геометричної прогресії q<1
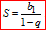
З допомогою цих формул можна обчислити до 90% задач на геометричну прогресію. 10% займають складні приклади з олімпіад, ЗНО тестів, де умови
ускладнюють до такої міри, що вчимо геометричну прогресію (г/п), а доводиться розв'язувати системи показникових рівнянь чи нерівності. З ними Ви познайомитеся в наступних уроказ, а зараз перегляньте відповіді до завдань із збірника для ЗНО підготовки.
Приклад 21.8 Записати формулу для обчислення n-го члена геометричної прогресії 4; 12; 36; …
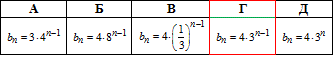 Обчислення: Маємо г/п, у якої b1=4, b2=12, b3=36 - члени г/п.
Обчислення: Маємо г/п, у якої b1=4, b2=12, b3=36 - члени г/п.
Знаходимо знаменник геометричної прогресії
q=b2/b1=12/4=3
Повторимо формулу для n-го член геометричної прогресії:
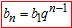 Підставляємо в неї свої значення
Підставляємо в неї свої значення
bn=4•3n-1
Відповідь: bn=4•3n-1 – Г.
В 9 класі кожен учень повинен вміти розв'язувати так приклади, це базис для обчислення всіх наступних завдань.
Приклад 21.9a Записати формулу для обчислення n перших членів геометричної прогресії 2; 6; 18; …
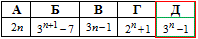 Обчислення: Маємо г/п, у якої b1=2, b2=6, b3=18 - члени г/п, тоді q=b2/b1=3 - знаменник.
Обчислення: Маємо г/п, у якої b1=2, b2=6, b3=18 - члени г/п, тоді q=b2/b1=3 - знаменник.
Обчислення n перших членів г/п рівносильне знаходженню суума геометричної прогресії:
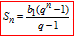
Підставляємо відомі значення та спрощуємо
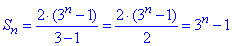
Відповідь: 3n-1 – Д.
Як бачите нічого складного немає і такі завдання на ЗНО під силу розв'язати кожному школяру.
Далі підуть задачі, для розв'язання яких потрібно логічно мислити або як кажуть "трохи подумати".
Приклад 21.20 У пробірці міститься три клітини, які розмножуються поділом навпіл.
Скільки утвориться клітин після n-го поділу?
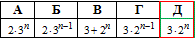
Обчислення: Навпіл є для Вас підказкою, що тут потрібно використовувати властивості геометричної прогресії.
Відомий b1=3 - перший її член прогресії (початкова кількість клітин) та
q=2 - знаменник (після кожного поділу клітин ставало вдвічі більше 3, 6, 12).
Кількість клітин, яка утвориться після n-го поділу є n+1 член г/п (це важливо розуміти), його розраховуємо з формули:
bn+1=b1 qn+1-1=3•2n.
Відповідь: 3•2n – Д.
Приклад 21.21 Вкладник вніс до банку a гривень під 10% річних.
Скільки грошей буде на рахунку вкладника через n років?
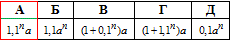
Обчислення: Задачі на вклади або банквські проценти в більшості випадків пов'язані з геометричною прогресією.
Позначимо A0=b1=a - перший член (початковий вклад),
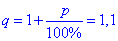 - знаменник (відсоткова ставка записано десятковим дробом p=10%).
- знаменник (відсоткова ставка записано десятковим дробом p=10%).
Кількість грошей, які будуть на рахунку вкладника через n років (на n+1 рік) є n+1 членом г/п.
Виконуємо підстановку у формулу
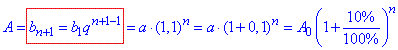
тобто A=1,1na.
В цьому завданні одночасно вивели формулу складних відсотків:
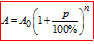
Відповідь: 1,1na – А.
Приклад 21.30 Установити відповідність між геометричними прогресіями (bn) (1–4), заданими двома членами, та формулами n-го члена (А–Д).

Обчислення: Алгоритм розв'язання такого сорту завдань наступний:
За формулою n-го члена геометричної прогресії складаємо одне або два показникових рівняння, далі виражаємо знаменник q та відновлюємо формулу bn. Після цього порівнюємо із заданими варантами А - Д в умовах тесту:
bn=b1q^(n-1).
1) b1=4, b4=108,
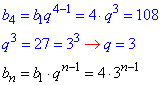
1 - Г.
2) b1=2, b4=-54,
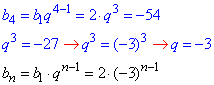
2 - А.
3) b2=-6, b5=-48
Складаємо систему показникових відносно q рівнянь
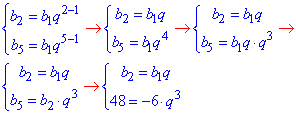
q3=-8=(-2)3 , звідси q=-2.
b2=b1q, b1=b2:q, b1=-6:(-2)=3, звідси b1=3.
bn=b1qn-1=3(-2)n-1.
3 - Б.
4) b2=6, b5=81/32
Схема обчислень аналогічна попередньому пункту
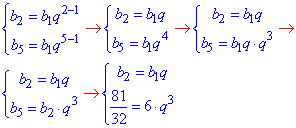
Останнє рівняння системи спрощуємо до кубічного
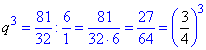
та знаходимо знаменник прогресії q=3/4.
b2=b1q, b1=b2:q, b1=6:(3/4)=6•4/3=8
bn=b1qn-1=8•(3/4)n-1.
4 - Д.
Завдання дещо важчі, але все тут зводиться до розв'язання системи 2 рівнянь та показникового рівняння не старше 4 порядку.
При q={2,-2,3,-3}, а такі найчастіше задаватимуть, це не є складно.
Приклад 21.43a У посудині міститься 1000 л повітря. Кожний рух поршня розріджувального насоса видаляє з посудини 0,1 частини повітря.
Скільки літрів повітря залишиться в посудині після п'яти рухів поршня?
Обчислення: Маємо геометричну прогресію (bn), у якої b1=1000 л - перший член (початковий об'єм повітря), q=0,9 - знаменник (кожний рух поршня насоса видаляє з посудини 0,1 частини повітря і тому кожного разу залишається 0,9 частина), n=6 - кількість членів г/п (після п'яти рухів поршня, означає на шостому русі).
Обчислимо об'єм повітря, який залишиться в посудині після п'яти рухів поршня як 6-й член геометричної прогресії
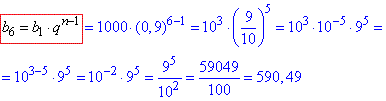
Відповідь: 590,49.
Поступово цей урок доповнимо цікавими прикладами на формулу n-го члена геометричної прогресії, а далі переходьте до завдань на знаходження знаменника та суми геометричної прогресії.


