Підсумуємо, що Ви на попередніх уроках навчилися обчислювати суми геометричної та арифметичної прогресій, різницю, знаменник, загальний член прогресій. Для знаходження сум рядів вводять поняття нескінченноспадної геометричної прогресії як геометричної прогресії зі знаменником меншим одиниці |q|<1 та нескінченною кількістю членів.
Якщо Вам задано q<1 і потрібно знайти суму скінченного числа членів геометричної прогресії то використовуйте одну з формул
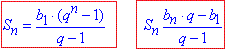 якщо n - необмежене, тобто при n→∞ маємо qn→0 і з формул вгорі виводимо наступну:
якщо n - необмежене, тобто при n→∞ маємо qn→0 і з формул вгорі виводимо наступну:
формула суми нескінченно спадної геометричної прогресії
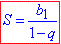 Незважаючи на простий вигляд формула дозволяє розв'язати багато завдань на прогресії, дослідження збіжності рядів також не обходиться без вказаної формули.
Незважаючи на простий вигляд формула дозволяє розв'язати багато завдань на прогресії, дослідження збіжності рядів також не обходиться без вказаної формули.
ЗНО тести, сума нескінченно спадної геометричної прогресії
Приклад 21.11 Знайти суму нескінченно спадної геометричної прогресії 3; -3/2; 3/4; -3/8; ...
А | Б | В | Г | Д |
2 | 3 | 6 | 2,5 | 1 |
Обчислення: Запишемо члени прогресії b1=3, b2=-3/2, b3=3/4, b4=-3/8 , та обчислимо знаменник
q=b2/b1=-1/2
Оскільки |q|=1/2<1, то маємо нескінченну спадну геометричну прогресію.
Суму прогресії знаходимо за спрощеною формулою:
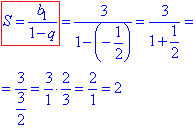
Ось такі завдання задають в 9, 10 класах і їх не важко розв'язати.
Відповідь: 2 – А.
Приклад 21.12 Обчислити суму 21-1+21-2+21-3+….
А | Б | В | Г | Д |
0,1 | 0,05 | 0,01 | 0,2 | 0,02 |
Обчислення: Обчислити значення виразу 21-1+21-2+21-3+ означає знайти суму нескінченно спадної геометричної прогресії, у якої b1=21-1=1/21 - перший член, q=21-1=1/21<1 - знаменник цієї прогресії.
За формулою знаходимо суму прогресії
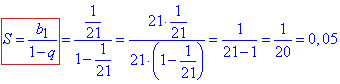 Остаточно, 21-1+21-2+21-3+…=0,05.
Остаточно, 21-1+21-2+21-3+…=0,05.
Відповідь: 0,05 – Б.
Приклад 21.18 Знайти знаменник нескінченно спадної геометричної прогресії, якщо її перший член b1=1/101, а сума - 1/100.
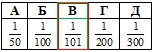 Обчислення: Маємо нескінченно спадну г/п, у якої b1=1/101 - перший член і S=1/100 - сума.
Обчислення: Маємо нескінченно спадну г/п, у якої b1=1/101 - перший член і S=1/100 - сума.
Для знаходження знаменника використаємо формулу: S=b1/(1-q).
Виконуємо розрахунки
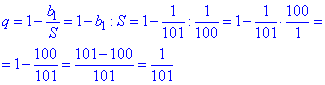
Звідси q=1/101 - знаменник нескінченно спадної г/п.
Відповідь: 1/101 – В.
Приклад 21.23 Установити відповідність між послідовностями (1–4) та їхніми можливими властивостями (А–Д).

Обчислення:
1. 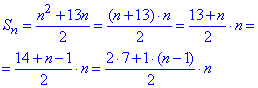
Отримали арифметичну прогресію із сумою
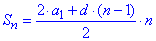
у якої a1=7 - перший член, d=1 - різниця, n - кількість членів.
1 - А.
2. Sn=3n+2 - послідовність часткових сум - не є прогресією.
2 - В.
3. an=2n=2•2n-1.
Отримали г/п із загальним членом bn=b1•qn-1, у якої
b1=2 - перший член, q=2 - знаменник (|q|>1), n - кількість членів.
3 - Г.
4. S=a1/(1-q).
Отримали нескінченно спадну геометричну прогресію із сумою Sn=b1/(1-q), у якої b1=a1 - перший член, q - знаменник (|q|<1). 4 - Б.
Нехай у геометричній прогресії маємо bn - загальний член, bn-1 - попередній член, bn+1 - наступний член.
Тоді знаменник геометричної прогресії можна знайти за формулою:
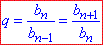 Звідси випливає наступна властивість членів прогресії:
Звідси випливає наступна властивість членів прогресії:
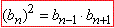
Приклад 21.32 Установити відповідність між нескінченними спадними геометричними прогресіями (bn) (1–4), заданими двома першими членами, та їх сумами (А–Д).
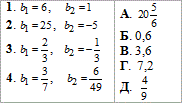
Обчислення: Такого типу завдання дозволяють перевірити наскільки добре Ви вмієте працювати з дробами, оскільки дроби доводиться спрощувати при обчисленні сум нескінченно спадних геометричних прогресій.
Алгоритм обчислень містить всього дві дії:
- Для заданих нескінченно спадних геометричних прогресій (bn) необхідно знайти знаменник q як частку другого до першого члена прогресії q=b2:b1.
- Далі записати суму за допомогою формули: S=b1/(1-q).
1) b1=6, b2=1. q=b2:b1=1/6
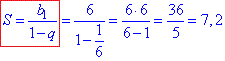 Звідси, S=7,2. 1 – Г.
Звідси, S=7,2. 1 – Г.
2) b1=25, b2=-5. q=b2:b1=-5/25=-1/5.
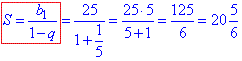 Отже, 2 - А.
Отже, 2 - А.
3) Використовуємо записаний на початку алгоритм
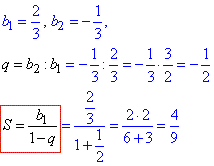
звідси q=-1/2.
S=4/9. 3 - Д.
4) 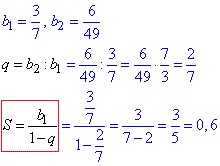
S=0,6. 4 - Б.
Приклад 21.42 (xn) - нескінченна спадна геометрична прогресія, у якої x1=3, q=1/3.
Знайти суму її членів з непарними номерами.
Обчислення: Маємо нескінченно спадну геометричну прогресію (xn), у якої x1=3 - перший член (непарний номер), q=1/3- знаменник.
Кожен наступний номер цієї прогресії у q разів більший за попередній, а кожен непарний номер - у q^2 більше за попередній непарний номер. Сума членів нескінченно спадної г/п з непарними номерами рівна:
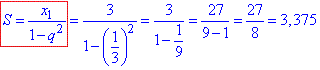 Відповідь: 3,375.
Відповідь: 3,375.
Приклад 21.44 Спростити рівняння функції 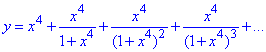 та знайти її значення, якщо x=3.
та знайти її значення, якщо x=3.
Обчислення: Оскільки 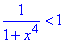 , то вираз
, то вираз
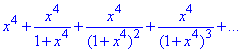
є нескінченно спадною геометричною прогресією, у якої b1=x^4 - перший член, q=1/(1+x^4) - знаменник.
Спростити рівняння функції рівносильне знайти суму нескінченно спадної геометричної прогресії (S=b1/(1-q))
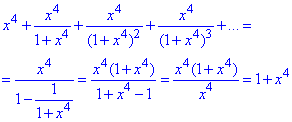
Отримали залежність y=1+x^4, звідси y(3)=1+3^4=1+81=82.
Відповідь: 82.
Приклад 21.41 Інфузорії-туфельки розмножуються поділом на дві частини.
Скільки утвориться інфузорій із п'яти після семи поділів?
Обчислення: Маємо задачу з біології на геометричну прогресію (bn), у якої b1=5 - перший член (початкова кількість інфузорій), q=2 - знаменник (у два рази збільшуються після кожного поділу), n=8 - кількість поділів.
Обчислюємо 8 член геометричної прогресії
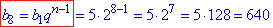
Після семи поділів (тобто на 8-й) утворилося 640 інфузорій-туфельок.
Відповідь: 640.
Якщо маєте цікаві завдання по темі, то надсилайте нам, тоді ми даний урок доповнимо.
А зараз можете перейти до відповідей №35-47 із ЗНО тестів на арифметичну прогресію.


