Дискримінант, як і квадратні рівняння починають вивчати у 8 клаcі в курсі алгебри. Розв'язати квадратне рівняння можна через дискримінант і за допомогою теореми Вієта. Методика вивчення квадратних рівнянь, як і формули дискримінанта досить невдало прищеплюються школярам, як і багато чого в теперішній освіті. Тому проходять шкільні роки, навчання в 9-11 класі заміняє "вища освіта" і всі знову шукають – "Як розв'язати квадратне рівняння?", "Як знайти корені рівняння?", "Як знайти дискримінант?" і ...
Формула дискримінанту
Дискримінант D квадратного рівняння a*x2 + bx + c=0 рівний D=b2 – 4*a*c.
Корені (розв'язки) квадратного рівняння залежать від знаку дискримінанту (D) :
D>0 – рівняння має 2 різних дійсних коренів;
D=0 - рівняння має 1 корінь (2 одинакові корені):
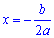
D<0 – не має дійсних коренів (в шкільній теорії). У ВУЗ-ах вивчають комплексні числа і вже на множині комплексних чисел рівняння з від'ємним дискримінантом має два комплексні корені.
Формула для обчислення дискримінанту досить проста, тому безліч сайтів пропонують онлайн калькулятор дискримінанту. Ми з такого роду скриптами ще не розібралися, тому хто знає, як це реалізувати просимо писати на пошту Ця електронна адреса захищена від спам-ботів. вам потрібно увімкнути JavaScript, щоб побачити її..
Загальна формула для знаходження коренів квадратного рівняння:
Корені рівняння знаходимо за формулою
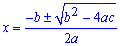
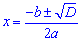Якщо коефіцієнт при змінній в квадраті парний то доцільно обчислювати не дискримінант, а четверту його частину
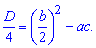В таких випадках корені рівняння знаходять за формулою
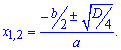
Другий спосіб знаходження коренів – це Теорема Вієта.
Формулюється теорема не тільки для квадратних рівнянь, а й для многочленів. Це Ви можете почитати у Вікіпедій чи других електронних ресурсах. Однак для спрощення розглянемо ту її частину, що стосується приведених квадратних рівнянь , тобто рівнянь вигляду (a=1)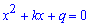 
Суть формул Вієта полягає в тому, що сума коренів рівняння рівна коефіцієнту при змінній, взятому з протилежним знаком. Добуток коренів рівняння рівний вільному члену. Формулами теорема Вієта має запис.
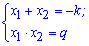Виведення формули Вієта достатньо просто. Розпишемо квадратне рівняння через прості множники
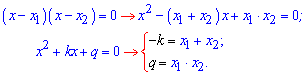Як бачите, все геніальне є одночасно простим. Найефективніше використовувати формулу Вієта коли різниця коренів за модулем або різниця модулів коренів рівна 1, 2. Наприклад, наступні рівняння за теоремою Вієта мають корені
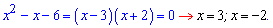
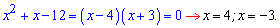
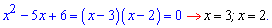
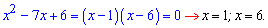
До 4 рівняння аналіз має виглядати наступним чином. Добуток коренів рівняння рівний 6, тобто коренями можуть бути значення (1; 6) та (2;3) або пари з протилежним знаком. Сума коренів рівна 7 (коефіцієнту при змінній з протилежним знаком). Звідси робимо висновок, що розв'язки квадратного рівняння рівні x=2; x=3.
Найпростіше підбирати корені рівняння серед дільників вільного члена, корегуючи їх знак з метою виконання формул Вієта. На початку це здається важко зробити, але з практикою на ряді квадратних рівнянь така методика виявиться ефективнішою за обчислення дискримінанту та знаходження коренів квадратного рівняння класичним способом.
Як бачите шкільна теорія вивчення дискримінанту та способів знаходження розв'язків рівняння позбавлена практичного змісту – "Для чого школярам квадратне рівняння?", "Який фізичний зміст дискримінанту?".
Давайте спробуємо розібратися, що описує дискримінант?
В курсі алгебри вивчають функції, схеми дослідження функції та побудови графіку функцій. І серед усіх функцій важливе місце займає парабола, рівняння якої можна записати у вигляді
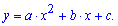Так от фізичний зміст квадратного рівняння – це нулі параболи, тобто точки перетину графіка функції з віссю Ox
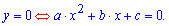Властивості парабол, які описані нижче попрошу Вас запам'ятати. Прийде час здавати екзамени, тести, чи вступні іспити і Ви будете вдячні за довідковий матеріал. Знак при змінній в квадраті відповідає чи будуть вітки параболи на графіку іти вгору (a>0),
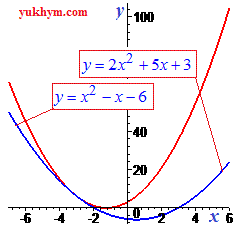
чи парабола вітками донизу (a<0).
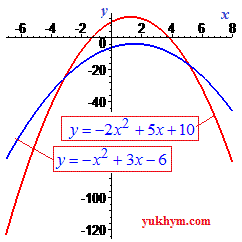
Вершина параболи лежить посередині між коренями
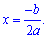
Фізичний зміст дискримінанту:
Якщо дискримінант більший нуля (D>0) парабола має дві точки перетину з віссю Ox.
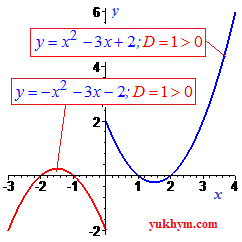Якщо дискримінант рівний нулю (D=0) то парабола у вершині дотикається до осі абсцис.
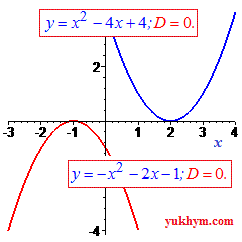
І останній випадок, коли дискримінант менший нуля (D<0) – графік параболи належить площині над віссю абсцис (вітки параболи вгору), або графік повністю під віссю абсцис (вітки параболи опущені донизу).
Неповніні квадратні рівняння
Якщо в квадратному рівнянні коефіцієнт при вільному члені або змінній рівні нулю то такі рівняння називають неповними. Корені рівнянь знаходимо за простішими формулами
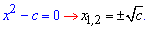Графік функцій завжди симетричний відносно початку координат. Варто зазначити, що рівняння має дійсні корені лише тоді коли в рівнянні чергуються знаки при коефіцієнтах "+, -" або "-, +".
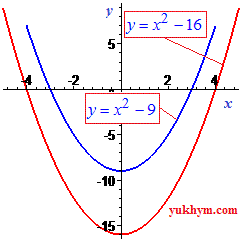
Неповне квадратне рівняння вигляду
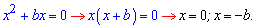
одним з коренів завжди має точку x=0.
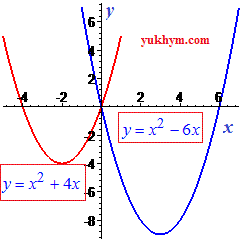В такому контексті розв'язування квадратних рівнянь стає потрібним, а при побудові графіків парабол, ще й візуально цікавим проведенням часу, особливо якщо йде мова про шкільні заняття з аналізу графіку функцій, чи вивченні теми парабол. Тому в 8, 9 класі рекомендуємо ці дві теми в алгебрі поєднувати.
Якщо матеріал допоміг Вам в навчанні, просьба поділитися з друзями посиланням на статтю !
