Готові відповіді до контрольної роботи з теорії ймовірностей допоможуть вивчити формули, методику розрахунків та ознайомитися з типовими завданнями на контрольних, індивідуальних роботах.
ВАРІАНТ – 1
Завдання 1 Із коробки, в якій 10 білих, 6 чорних та 4 синіх кульок, навмання виймають 3 кульки. Знайти ймовірність того, що серед них будуть:
- а) всі білі;
- б) перша біла, далі дві чорні;
- в) одна біла, одна чорна, одна синя.
Розв'язання: Число всіх можливих подій – кількість способів, за якими можна вибрати 3 кульки з 20 (10+6+4) знаходимо через розміщення:
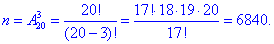
а) Число сприятливих подій – кількість способів, за якими можна вибрати 3 білі кульки з 10 можливих:
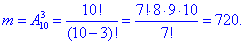
Ймовірність події A, при якій виймають усі білі кульки рівна
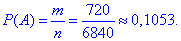
б) Число сприятливих подій – кількість способів, за якими можна вибрати одну білу кульку з 10 і дві чорних кульок з 6 можливих:
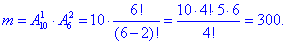
Ймовірність події B, при якій виймають 1 білу і дві чорні кульки:
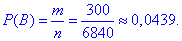
в) Число сприятливих подій – кількість способів, за якими можна вибрати 1 білу з 10, 1 чорну з 6 і 1 синю кульку з 4:
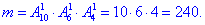
Ймовірність події C, при якій виймають 1 білу, 1 чорну і 1 синю кульки:
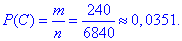
Наведені відповіді є правильними згідно формул теорії ймовірності, однак не так очевидними для студентів та школярів, важка для розуміння є методика обчислення. Існує геометричний спосіб вирішення даної задачі. Покажемо його переваги.
а) Для першого пункту нам важливо, що маємо 10 білих кульок з 20, а потрібно вибрати 3.
Першу кульку можна вибрати 10 способами з 20, тому ймовірність вийняти першою білу кульку рівна p1=10/20. Після цього залишиться 9 білих кульок з 19, тобто ймовірність що друга кулька буде білого кольору рівна p2=9/19. І останню, третю можна вибрати з ймовірністю p3=8/18.
За правилом сумування ймовірностей нам потрібно знайти їх добуток
p=p1*p2*p3=10/20*9/19*8/18=2/19=0,10526.
б) Одну білу (з 10) і дві чорні (з 6) при 20 кульках можна вибрати з ймовірністю
p=10/20*6/19*5/18=5/144=0,04386.
При цьому неважливо чи білу кульку вибираємо першою чи другою, чи третьою. Якщо поглянути на формулу, то поміняються місцями лише чисельники. Загалом ймовірність від цього не поміняється.
в) Враховуючи, що від порядку входження добуток ймовірностей не змінюється знаходимо значення для третього випадку
p=10/20*6/19*4/18=2/57=0,3509.
Останній метод можете застосовувати для контролю правильності обчислень за формулами теорії ймовірності.
Завдання 2 Для обслуговування деякого будівництва виділено 5 автомобілів. За однакових і незалежних умов з ймовірністю 0,8 вони прибувають на будівництво. Знайти ймовірність того, що в даний момент будівництво обслуговують
- а) всі п'ять автомобілів;
- б) не менше трьох;
- в) жодний автомобіль не прибув на обслуговування.
Розв'язання: Нехай pi=0,8 - ймовірність того, що і-й автомобіль прибув на будівництво, тоді qi=1-pi=1-0,8=0,2 - ймовірність того, що автомобіль не прибув (i=1,2,3,4,5).
а) Ймовірність того, що всі п'ять автомобілів прибули на будівництво
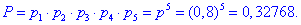
б) Ймовірність того, що не менше трьох автомобілів прибули на будівництво означає або 3, або 4, або 5.
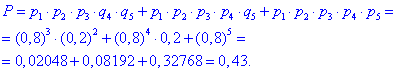
На перший погляд все логічно, але насправді - не зовсім так.
Машини різні, тоді виходить, що важливо які саме дві не приїхали в першому випадку, і яка одна в другому.
А з формули слідує, що 4-та і 5-та не приїхали в першому випадку, та 5 - в другому.
А могли не приїхати 1 і 3, або 2 і 4, і т.д в першому випадку та одна з 5 машин в другому випадку.
Тому в наведеній вище формулі перший доданок слід домножити на С52=10, а другий на С51=5.
Тоді ймовірність рівна
P=10*0,02048+5*0,08192+0,32768=0,94208.
Уважно перегляньте, та обдумайте чому саме так.
в) Ймовірність того, що жодний автомобіль не прибув на будівництво знаходимо за формулою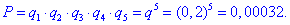 
На цьому завдання розв'язано.
Завдання 3 На трьох лініях заводу залізобетонних виробів при однакових і незалежних умовах виготовляються конструкції однієї назви, причому: перша лінія випускає 60%, друга – 30%, третя – 10% всіх виробів. Ймовірність, що кожна конструкція є небракованою відповідно для першої лінії 0,8, для другої – 0,7, для третьої – 0,4.
Знайти ймовірність, якщо
- а) конструкція, що знаходиться під навантаженням, є небракованою;
- б) за умови, що вона небракована, знайти ймовірність того, що її виготовлено на третій лінії.
Розв'язання: Задача на формулу повної ймовірності та Байєса. Нехай Hi - гіпотези, що виріб виготовлений і-м робітником, де i=1,2,3. Тоді ймовірність кожної з гіпотез рівна частці продукції в загальній кількості:
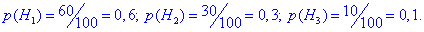
Їх сума рівна повній ймовірності, тобто одиниці. Нехай подія A полягає в тому, що взята навмання конструкція є небракована. Тоді на основі умови можемо виписати ймовірності того, що небраковану конструкцію виготовлено на кожній лінії:
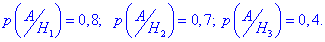
а) За формулою повної ймовірності знаходимо ймовірність, що конструкція, що знаходиться під навантаженням, є небракованою:
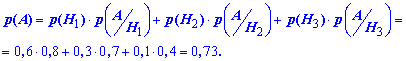
б) Ймовірність того, що конструкцію виготовлено на третій лінії рівна вкладу третього доданку в попередній формулі. Якщо записати це формулами ймовірності, то отримаємо
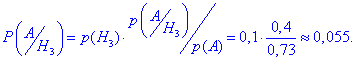
Подібних прикладів на ймовірність Байєса можна навести безліч. На контрольній чи індивідуальній вони є поширені, тому запам'ятайте формули.
Завдання 4 Монету кинуто 100 разів. Знайти ймовірність того, що герб випаде:
- а) 60 разів;
- б) не менше 40 і не більше 90.
Розв'язання: а) Оскільки ймовірність не залежить від історії (попередніх дослідів): p=0,5, то за формулою Бернуллі (дає точне значення) знаходимо
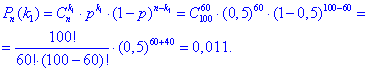
Однак для таких великих факторіалів слід виконувати обчислення в математичному пакеті – Maple, Mathematica, MathCad. Наближене значення ймовірності дає локальна теорема Лапласа.
Оскільки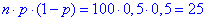 
, то похибка формул мінімальна
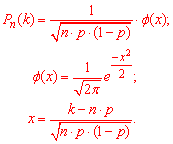Виконаємо обчислення: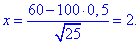 
За таблицями табулювання локальної функції Лапласа маємо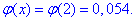 
Ймовірність рівна
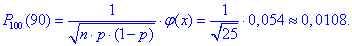
Як бачимо, розбіжність зі значенням отриманим за формулою Бернуллі незначне!
б) Ймовірність, що не менше 40 і не більше 90 разів випаде герб знайдемо за інтегральною формулою Лапласа:
де 
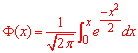- інтегральна функція Лапласа;
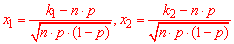- аргументи інтегральної функції розподілу.
Знайдемо точки
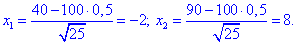
Отож ймовірність рівна 0,977.
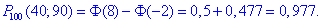
На цьому обчислення завершено.
Завдання 5 Монету кинуто чотири рази (n=4). X - число появ герба. Знайти закон розподілу випадкової величини X, знайти математичне сподівання випадкової величини M(X), дисперсію D(X), середньоквадратичне відхилення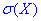 
, функцію розподілу F(X) та побудувати її графік.
Розв'язання: Оскільки від досліду до досліду ймовірність залишається сталою (а саме p=0,5 і q=1-0,5=0,5), то ймовірність випадання герба змінюється за біноміальним законом:
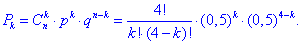
Результати запишемо в таблицю:
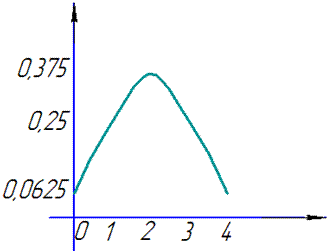
Графік закону розподілу має вигляд
Математичне сподівання випадкової величини
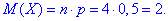
Знаходимо дисперсію
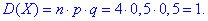
Середнє квадратичне відхилення випадкової величини X:
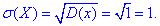
Функцію розподілу випадкової величини X знайдемо за формулою:
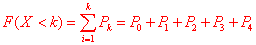
Результати запишемо в таблицю:
Графік функції розподілу має вигляд
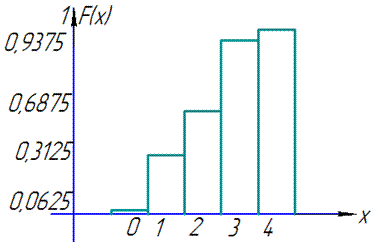
Завдання 6 Випадкова величина задана щільністю розподілу f(x):
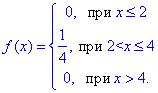
Знайти функцію розподілу F(X), математичне сподівання випадкової величини M(X), дисперсію D(X) випадкової величини та ймовірність того, що в результаті випробувань x набуде значень, що належать інтервалу (2,5;3). Побудувати графіки f(x) та F(x).
Розв'язання: Ітегруванням знаходимо функція розподілу:
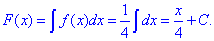
Графік функції f(x) та F(x) (при C=0):
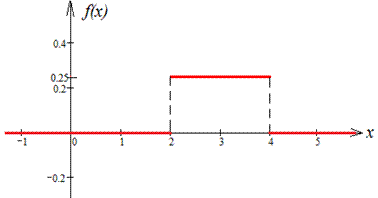
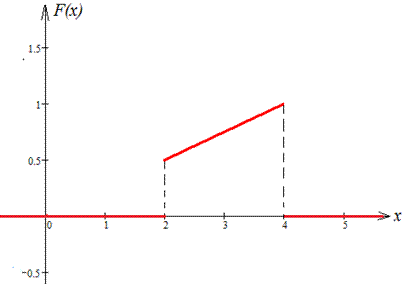
Через інтеграл знаходимо математичне сподівання:
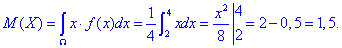
Далі дисперсію:
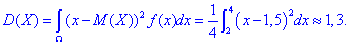
Ймовірність того, що в результаті випробувань x набуде значень, що належать інтервалу (2,5;3) знаходимо інтегруванням:
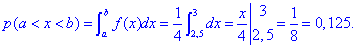
Ось так потрібно пояснювати подібні задачі.
Завдання 7 Відомі математичне сподівання a=1 та середнє квадратичне відхилення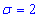 
випадкової величини x, яка розподілена нормально. Обчислити ймовірність того, що
- а) ця випадкова величина прийме значення, які належать інтервалу
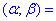(0;4); - б) абсолютна величина відхилення |x-a| буде менше за 5 (
).
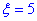Розв'язання: а) Для знаходження імовірності того, що випадкова величина x прийме значення, які належать інтервалу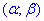 
скористаємось формулою Лапласа:
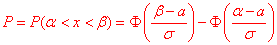Де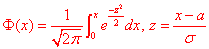 
- інтегральна функція Лапласа (її значення є в таблиці).
Виконуємо обчислення ймовірності
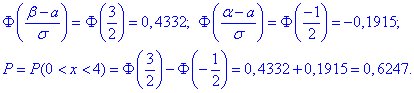
б) Для знаходження імовірності того, що абсолютна величина відхилення |x-a| <5 буде менше за 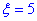скористаємось формулою:
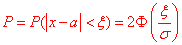
Знаходимо складову
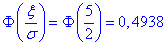
та обчислюємо ймовірність
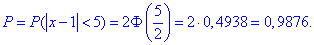
Після таких пояснень до контрольної чи індивідуальної роботи у викладачів не залишиться до Вас ніяких зауважень. Тож вчіть методику знаходження ймовірності в кожному з випадків та застосовуйте знання на практиці.
