Готові відповіді допоможуть навчити вирішувати типові контрольні та індивідуальні роботи на класичну ймовірність, формули Бернуллі, Байєса, локальну та інтегральну теорему Лапласа. Завдання корисні для студентів 1, 2 курсу навчання.
ВАРІАНТ – 5
Завдання 1. В бригаді 20 робітників, серед яких 11 дівчат, решта хлопці. На нараду послали 4-х представників від бригади. Знайти ймовірність того, що серед них:
- а) одні чоловіки;
- б) одні жінки;
- в) дві жінки і 2 чоловіка.
Розв'язання: Число всіх можливих подій – кількість способів, за якими можна вибрати чоирьох представників з 20 осіб:
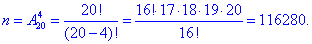
а) Число сприятливих подій – кількість способів, за якими можна вибрати 4-х хлопців із 9 можливих:
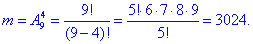
Ймовірність події A, при якій на нараду відправляють 4-х хлопців:
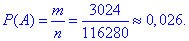
б) Число сприятливих подій – кількість способів, за якими можна вибрати чотирьох дівчат із 11 можливих:
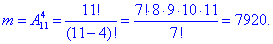
Ймовірність події B, при якій на нараду відправляють чотирьох дівчат:
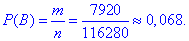
в) Число сприятливих подій – кількість способів, за якими можна вибрати 2-х жінок з 11 і 2-х чоловіків з 9:
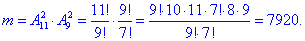
Ймовірність події C, при якій на нараду відправляють 2-х жінок і 2-х чоловіків:
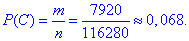
Відповіді можна знайти і геометричним способом. Покажемо, як його реалізувати на практиці.
а) ймовірність, що першим вибрали когось з чоловіків рівна p1=9/20, оскільки маємо 9 чоловік серед 20. Після того, як одного вибрали матимемо 8 чоловіків серед 19, що залишилися. Таким чином, ймовірність що другим виберуть чоловіка рівна p2=8/19. Третього - p3=7/18, та четвертого p4=6/17. За правилом сумування ймовірностей знаходимо їх добуток
P(A)=9/20*8/19*7/18*6/17=42/1615=0,026.
б) Виконавши подібні міркування, прийдемо до ймовірності
P(B)=11/20*10/19*9/18*8/17=22/323=0,068.
в) Дві жінки і два чоловіки можна вибирати кількома способами - ЧЧЖЖ, ЧЖЧЖ, ЖЖЧЧ, ЖЧЧЖ,..
Ймовірність при цьому не зміниться, оскільки знаменник спадає на одиницю з кожним новим добутком, а в чисельнику множники змінюються місцями. Для прикладу, остання записана комбінація матиме ймовірність
P(С)=11/20*9/19*8/18*10/17=22/323=0,068.
Якщо викладачі вимагають користуватися формулами ймовірності - використовуйте перший спосіб, другий в решті випадків (для перевірки).
Завдання 2. Троє студентів складають іспит. Ймовірність, що 1-й студент складе іспит дорівнює 0,8, 2-й – 0,7, 3-й – 0,4. Обчислити ймовірність того, що не складуть іспит:
- а) всі студенти;
- б) тільки один;
- в) хоча б один.
Розв'язання: Нехай p1=0,8, p2=0,7, p3=0,4 - ймовірність того, що іспит складуть відповідно 1-й, 2-й і 3-й студент, тоді для протилежної події q1=1-p1=0,2, q2=1-p2=0,3, q3=1-p3=0,6 - ймовірністі того, що іспит не складуть відповідно 1-й, 2-й і 3-й студенти.
а) Ймовірність того, що іспит не складуть всі студенти рівна добутку:
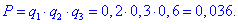
б) Ймовірність того, що іспит не складе тільки один студент рівна трьом варіантам з "або":
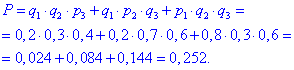
Якщо розписати словами, то або третій або другий або перший студент складе іспит з усіх.
в) Ймовірність того, що іспит не складе хоча б один студент є протилежною подією, що іспит не складуть усі студенти:
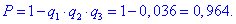
Це найпростіший варіант, оскільки в іншому випадку потрібно сумувати багато ймовірностей з умовою "або". Для перевірки можете переконатися, що довший за часом варіант розрахунків дає такий самий результат.
Завдання 3. На складі в трьох ящиках знаходяться деталі для ремонту автомобілів. Відомо, що в першому ящику 50 деталей, з яких 6 бракованих, у другому – 30 деталей, з яких 5 бракованих, у третьому – 40 деталей, з яких 6 бракованих. Майстер навмання вибирає деталь з будь-якого ящика. Знайти ймовірність того, що взята деталь бракована, й того, що майстер взяв її з другого ящика.
Розв'язання: Задача на застосування формули повної ймовірності та Байєса. В першому ящику 12% бракованих деталей, в другому – 16,67%, в третьому – 15% бракованих. Нехай Hi - гіпотези, що виріб виготовлений і-м робітником, де i=1,2,3. Тоді ймовірність кожної з гіпотез рівна частці виробів в загальній сукупності:
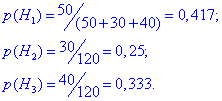
Їх сума рівна повній ймовірності =1. Нехай подія A полягає в тому, що взята навмання деталь бракована. Тоді на основі умови можемо виписати ймовірності того, що браковану деталь взято з кожного ящика:
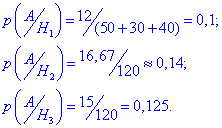
За формулою повної ймовірності знаходимо ймовірність, що деталь бракована:
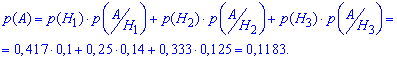
Ймовірність того, що бракована деталь взята з другого ящика за формулою Байєса рівна
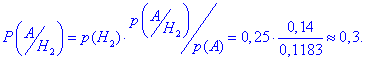
Це фактично вклад другого доданку в попередній сумі.
Завдання 4. Ймовірність народження хлопчика дорівнює 0,51. Знайти ймовірність того, що серед 100 народжених:
- а) рівно 50 хлопчиків;
- б) не менше 30 і не більше 70.
Розв'язання: а) Оскільки ймовірність не залежить від історії (попередніх дослідів), то за формулою Бернуллі знаходимо
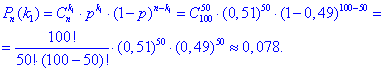
Значення розраховане в математичному пакеті Mathematica.
Наближене значення ймовірності дає локальна теорема Лапласа. Оскільки число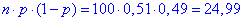 достатнє для застосування формули, то її похибка мінімальна
достатнє для застосування формули, то її похибка мінімальна
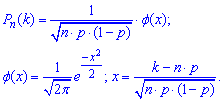
Виконаємо обчислення:
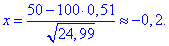
За таблицями табулювання локальної функції Лапласа маємо 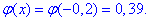
Ймовірність рівна
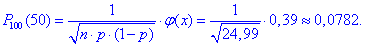
Як можете переконатися, відхилення від значення отриманого за формулою Бернуллі мале!
б) Ймовірність, що народилось від 30 і до 70 хлопців знайдемо за інтегральною формулою Лапласа:
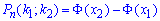
де 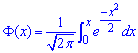 - інтегральна функція Лапласа;
- інтегральна функція Лапласа;
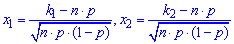 - аргументи інтегральної функції розподілу.
- аргументи інтегральної функції розподілу.
Знайдемо точки
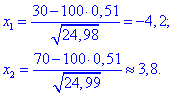
Отож ймовірність вірна
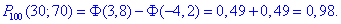
Завдання 5. В білеті чотири запитання (n=4). З ймовірністю 0,4 студент правильно відповідає на кожне з них. X - число правильних відповідей студента. Знайти закон розподілу випадкової величини X, знайти математичне сподівання випадкової величини M(X), дисперсію D(X), середньоквадратичне відхилення 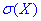 , функцію розподілу F(X) та побудувати її графік.
, функцію розподілу F(X) та побудувати її графік.
Розв'язання: Оскільки від досліду до досліду ймовірність залишається сталою (а саме p=0,4 і q=1-p=0,6), то ймовірність відповідати правильно на запитання змінюється за біноміальним законом:
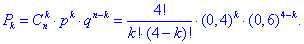
Результати запишемо в таблицю розподілу ймовірностей:
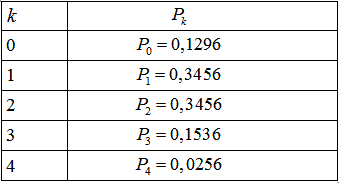
Графік закону розподілу має вигляд
 Математичне сподівання випадкової величини
Математичне сподівання випадкової величини
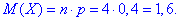
Дисперсія
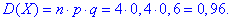
Середнє квадратичне відхилення випадкової величини X:
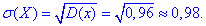
Функцію розподілу випадкової величини X знайдемо за формулою:
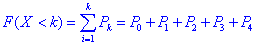
Результати запишемо в таблицю:
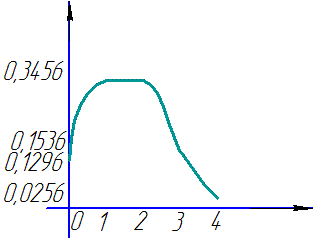
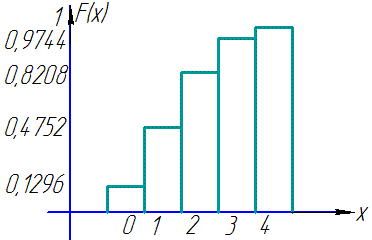
 Графік функції розподілу має вигляд
Графік функції розподілу має вигляд
Обчислення не складні і формули під силу вивчити кожному.
Завдання 6. Випадкова величина задана щільністю розподілу f(x):
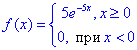
Знайти функцію розподілу F(X), математичне сподівання випадкової величини M(X), дисперсію D(X) випадкової величини та ймовірність того, що в результаті випробувань x набуде значень, що належать інтервалу (a;b). Побудувати графіки f(x) та F(x).
Розв'язання: Функція розподілу:
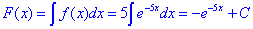
Графік функції f(x) та F(x) (при C=0):
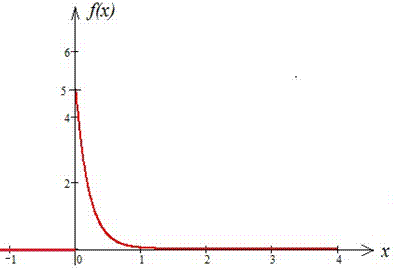
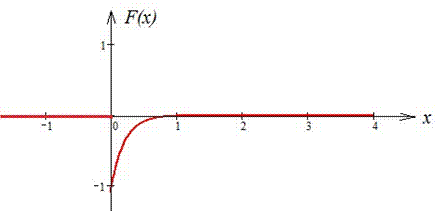
Математичне сподівання:
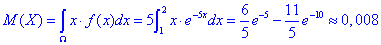
Дисперсія:
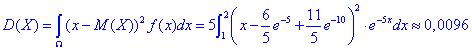
Ймовірність того, що в результаті випробувань x набуде значень, що належать інтервалу (a;b): 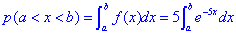
Завдання 7 Відомі математичне сподівання a=5 та середнє квадратичне відхилення 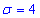 випадкової величини x, яка розподілена нормально. Обчислити ймовірність того, що
випадкової величини x, яка розподілена нормально. Обчислити ймовірність того, що
- а) ця випадкова величина прийме значення, які належать інтервалу
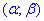 =(0;6);
=(0;6); - б) абсолютна величина відхилення |x-a|<9 буде менше за
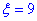 .
.
Розв'язання: а) Для знаходження імовірності того, що випадкова величина x прийме значення, які належать інтервалу 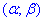 скористаємось формулою:
скористаємось формулою:
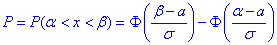
де 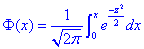 - інтегральна функція Лапласа (її значення є в таблиці).
- інтегральна функція Лапласа (її значення є в таблиці).
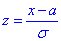 - заміна змінних.
- заміна змінних.
Отож, маємо
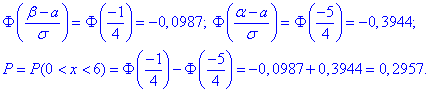
б) Для знаходження імовірності того, що абсолютна величина відхилення |x-a|<9 буде менше за 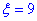 скористаємось формулою:
скористаємось формулою:
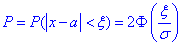
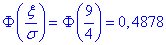
тому ймовірність
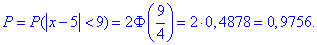
Попереду Вас чекає безліч готових відповідей з контрольних та індивідуальних робіт з теорії ймовірностей.


