Формула Гаусса-Остроградського застосовують для перетворення об'ємного (потрійного) інтеграла до інтегралу по замкнутій поверхні (подвійний) перетворення об'ємного (потрійного) інтеграла до інтеграла по замкнутій поверхні (подвійний), і навпаки:
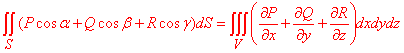
Інше застосування для обчислення потоку векторного поля через замкнену поверхню через інтеграл від дивергенції цього поля за об'ємом, що обмежений цією поверхнею.
Далі будуть наведені приклади переходу від подвійного до потрійного інтеграла, розставлення меж та обчислення об'ємних інтегралів.
Приклад 1 Використовуючи формулу Гаусса-Остроградського, перетворити поверхневий інтеграл
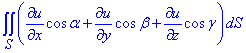
якщо гладка поверхня S обмежує скінченний об'єм V і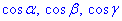 
- напрямні косинуси зовнішньої нормалі до поверхні S.
Розв'язання: Поверхневий інтеграл 2-го роду зводиться до потрійного інтеграла за допомогою формули Гаусса-Остроградського:
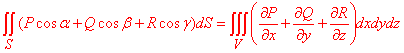
де P, Q, R виписуємо з заданого інтегралу
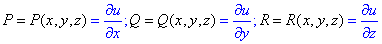- часткові похідні функції.
Тоді повторно обчислюємо похідні, щоб отримати напрямні косинуси в напрямку кожної з осей
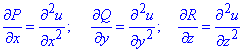
Можемо перейти від подвійного інтегралу до потрійного
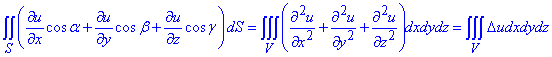
тут позначили Δu - дельта оператор Лапласа
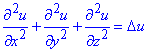
На цьому всі пояснення до першого прикладу.
Приклад 2 Використовуючи формулу Гауса-Остроградського, перетворити поверхневий інтеграл
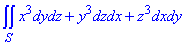
якщо гладка поверхня S обмежує скінченний об'єм V і 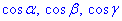- напрямні косинуси зовнішньої нормалі до поверхні S.
Розв'язання: Поверхневий інтеграл 2-го роду зведемо до трьохкратного інтегралу, використовуючи формулу Гауса-Остроградського:
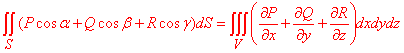
де P=P(x,y,z)=x3, P=P(x,y,z)=y3, P=P(x,y,z)=z3 беремо з умови.
О,числюємо другі похідні по "ікс, ігрик, зет"
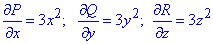
Записуємо формулу переходу від подвійного до потрійного інтегралу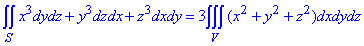 
На цьому прикладі Ви бачите, що сам перехід між кратними та потрійними інтегралами знайти не важко. Значно більше обчислень буде коли потрібно розставити межі та знайти потрійний інтеграл.
Приклад 3 Використовуючи формулу Гауса-Остроградського, перетворити поверхневий інтеграл
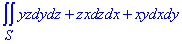
якщо гладка поверхня S обмежує скінченний об'єм V і 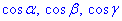- напрямні косинуси зовнішньої нормалі до поверхні S.
Розв'язання: Поверхневий інтеграл 2-го роду зведемо до потрійного інтегралу, використовуючи формулу Гауса-Остроградського: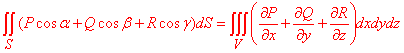
де P=P(x,y,z)=yz, Q=Q(x,y,z)=xz, R=R(x,yxz)=xy.
Часткові похідні другого порядку від P, Q, R
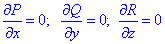
Тому потрійний інтеграл рівний нулю
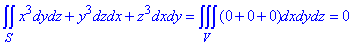
Приклад 4 Використовуючи формулу Гауса-Остроградського, обчислити поверхневий інтеграл int[x3dydz+y3dzdx+z3dxdy, S]
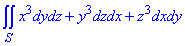
де S- зовнішня сторона сфери x2+y2+z2=a2.
Розв'язання: Поверхневий інтеграл ІІ роду зведемо до трьохкратного інтеграла, використовуючи формулу Гауса-Остроградського:
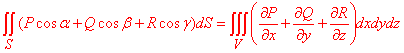
Виписуємо P=P(x,y,z)=x3, Q=Q(x,y,z)=y3, R=R(x,y,z)=z3.
Тоді часткові похідні від P, Q, R рівні
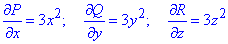
Область S обмежує об'єм сфери V рівнянням:
x2+y2+z2=a2.
В декартовій системі координат обчислювати потрійний інтеграл коли об'єм обмежений сферою недоцільно, оскільки матимемо кореневі функції в границях інтегралу.
Тому усюди перейдемо до сферичної системи координат:
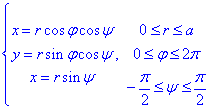
Знаходимо часткові похідні першого порядку за кутами від параметризованих координат
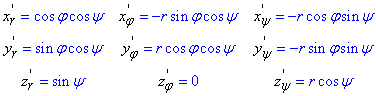
Додатково слід знайти якобіан переходу:
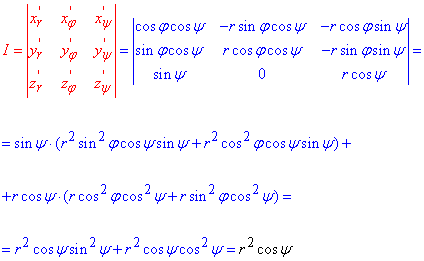
Він слугує додатковим множником в інтегралі.
Обчислимо підінтегральний вираз в нових координатах:
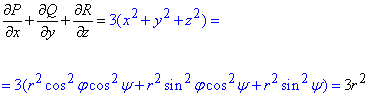
Далі використовуючи формулу Гауса-Остроградського знаходимо поверхневий інтеграл другого роду:
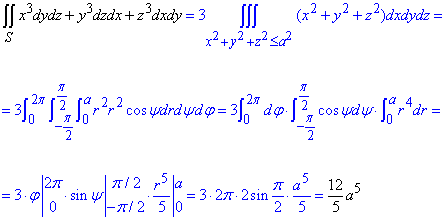
Уважно перегляньте як розкривали внутрішні інтеграли в потрійному.
Приклад 5 Використовуючи формулу Гаусса-Остроградського, перетворити поверхневий інтеграл
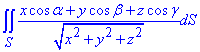
якщо гладка поверхня S обмежує скінченний об'єм V і 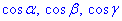- напрямні косинуси зовнішньої нормалі до поверхні S.
Розв'язання: Маємо поверхневий інтеграл ІІ роду
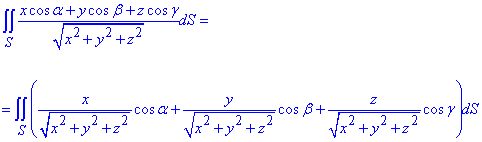
Зведемо до об'ємного інтеграла, використовуючи формулу Гауса-Остроградського: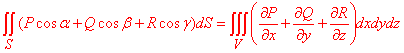
Відповідно до умови функції P, Q, R приймають значення
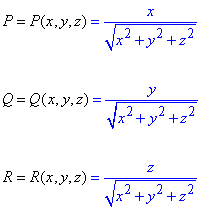
Обчислюємо часткові похідні другого порядку за змінними x, y, z
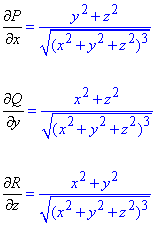
Підставляємо та перетворюємо інтегрування по площі на інтегрування по об'єму
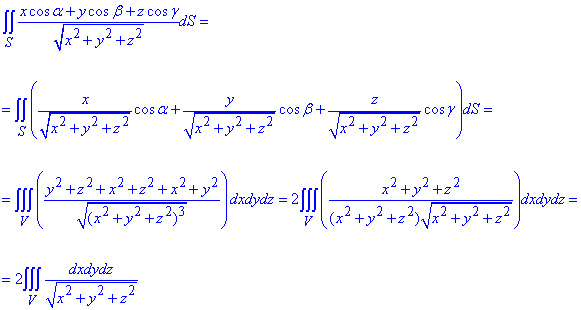
На сайті розміщено сотні розв'язаних прикладів з інтегрування, які охоплюють увесь курс з інтегралів.
Все що потрібно для навчання містить категорія інтегрування!
