Ниже приведены примеры интегрирования, каторые охватывают значительную часть разнообразных способов нахождения неопределенного интеграла. Такого типа примеры интегрирования функций Вы чаще всего увидите на 1,2 курсах учебы из высшей математики. Ниже приведены ответы одновременно и объясняют методику взятия интегралов, и служат инструкцией по их вычислению. Чтобы сэкономить время и место самих условий до примеров мы не выписывали.
Пример 1. Если бы перед интегралом имели множителем "икс", то его можно было бы внести под дифференциал и провести замену переменных.
Однако интеграл более сложен, потому выражения в скобках подносим к кубу, а дальше выполняем интегрирование каждого из слагаемых.
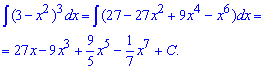
Пример 2. Задана дробная функция в знаменателе которой содержится иррациональность. Чтобы от нее избавиться функцию под корнем обозначим за новую переменную, дальше находим ее дифференциал и подставляем в интеграл. После незначительных манипуляций с показателями вычисляем интеграл, и вместо переменной подставляем выполненную замену.
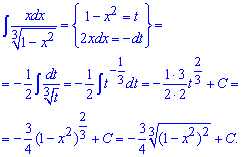
Пример 3. Кто часто вычисляет интегралы или хорошо знает теорию интегралов, то в этом и подобных заданиях за новую переменную выбирает логарифм. При дифференцировании логарифма получаем единицу разделенную на "икс", который значительно упрощает дальнейшее интегрирование.
Напоследок не забывайте в примерах на замену переменных перейти к начальной переменной "икс".
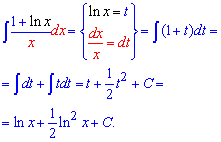
Пример 4. Выполняем интегрирование частями, для этого синус вносим под дифференциал
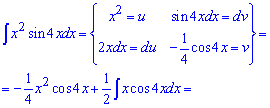
После первого раза опять получим интеграл, который вычисляем интегрированием частями.
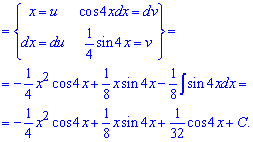
Пример 5. Имеем задание под правило интегрирования частями u*dv. За переменную выбираем экспоненту, а синус вносим под дифференциал.
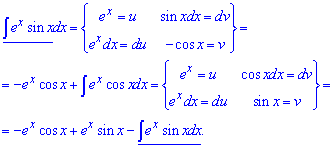
После повторного интегрирования частями придем к рекуррентной формуле, из которой и определяем интеграл.
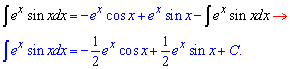
Пример 6. В этом интеграле квадратный трехчлен, который стоит в знаменателе надо возвести к сумме или разнице квадратов.
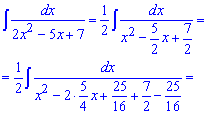
Дальше за формулами интегрирования получим арктангенс.
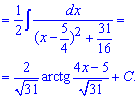
Пример 7. Интегрирование произведения тригонометрических функций дается не всем студентам, и здесь нужно учитывать как степени, так и сам вид функций.
В этом примере один косинус нужно внести под дифференциал и свести задание к интегрированию функции от синуса.
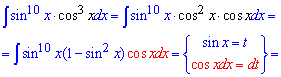
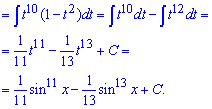
Сам интеграл не сложен и находится по правилу степенных функций .
Пример 8. Если имеем синусы или косинусы в показателях больше единицы, то за тригонометрическими формулами их надо расписать вплоть до первой степени. Дальше применяют формулы интегрирования синусов или косинусов.
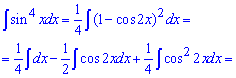
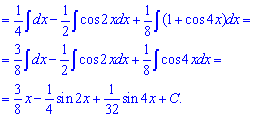
Пример 9. Чтобы найти интеграл от дробной функции сначала разделим числитель на знаменатель, и полученную в остатке дробь распишем на самые простые дроби. После этого, используя формулы интегрирования, вычисляем значение каждого из интегралов.
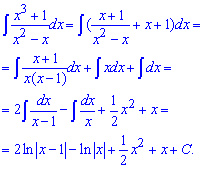
Пример 10. Имеем интеграл от дробной функции
![]()
Записываем ее через самые простые дроби первого и второго типов.
![]()
Дальше возводим дроби под общий знаменатель и из условия равенства числителей складываем систему линейных уравнений для вычисления неизвестных постоянных.
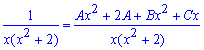
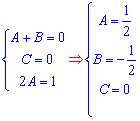
После ее решения возвращаемся к дроби, подставляем сталые и выполняем интегрирование.
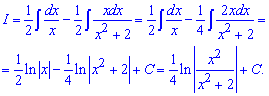
Пример 11. Имеем интеграл от дробной иррациональной функции. Для раскрытия иррациональности выполняем следующую замену переменных под интегралом
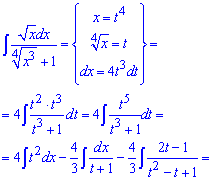
В результате придем к дробной рациональной функции под интегралом, которую расписав на простые дроби легко проинтегрировать.
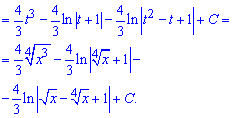
Пример 12. В этом задании чтобы избавиться иррациональности под интегралом необходимо использовать одну известную схему.
Она заключается в том, что проведя следующую замену переменных придем к рациональной функции от косинуса.
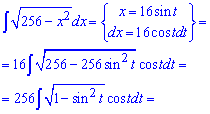
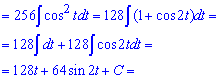
После интегрирования возвращаемся к выполненной замене и на этом вычислению можно завершить.
Однако, если иметь под рукой тригонометрические формулы то ответ можно упростить и записать в более компактном виде.
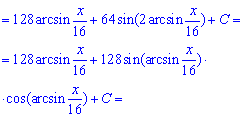
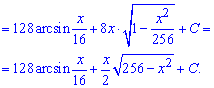
Пример 13. Имеем в знаменателе рациональную функцию от косинуса и синуса. Такие интегралы следует находить через универсальную тригонометрическую замену t=tg (x/2)
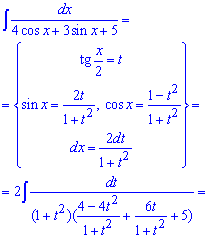
После подстановки формул синус и косинуса через тангенс половины кута подинтегральная функция превратится к дробной, в знаменателе которой будем иметь квадратный трехчлен. Его возводим к квадрату выражения, которое содержит переменную и интегрируем по правилу степенных функций .
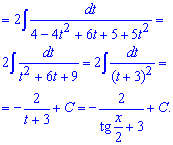
После интегрирования не забываем, что наше t=tg (x/2) и подставляем его в формулу интеграла.
На этом подборка примеров завершается, больше примеров Вы найдете в категории интегрирования.
Для увеличения базы готовых интегралов присылайте интересные примеры на Этот адрес электронной почты защищён от спам-ботов. У вас должен быть включен JavaScript для просмотра. или заказывайте у нас решение контрольных и расчетных работ.


