В даному уроці будуть розглянуті інтеграли вигляду R(sin(x), cos(x))
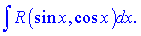
Такий запис вказує на те, що над синусом і косинусом проводяться виключно раціональні операції: додавання та віднімання, множення на константи, піднесення до цілого степеня, ділення. Простіше кажучи підінтегральна функція - це раціональна функція від синуса та косинуса.
Такі інтеграли зводяться до інтегралів від раціональної функції нового аргументу t підстановкою, яку ще називають універсальною:
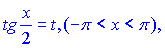тоді
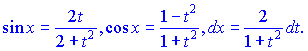Бувають випади, коли ця підстановка приводить до складних інтегралів. Тому для ряду випадків, в силу парності чи непарності підінтегральної функції, існують більш прості підстановки:
а)u=cos(x), якщо R(-sin (x), cos (x))= - R(sin (x), cos (x))
б) u=sin(x) якщо R(sin (x), -cos (x))= - R(sin (x), cos (x))
в) u=tan(x) якщо R(-sin (x), -cos (x))= R(sin (x), cos (x))
Приклади інтегрування раціональних фукцій від синуса та косинуса
Приклад 1. Обчислити інтеграли
а)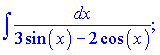 
Розв'язок. Застосуємо універсальну тригонометричну підстановку
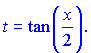
На її основі перетворюємо синус та косинус до вигяду
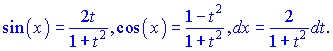
Підставимо в інтеграл та проінтегруємо за новою змінною
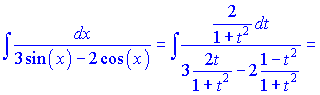
В знаменнику в вадратичній функції виділяємо різницю квадратів, щоб звести під логарифм частки
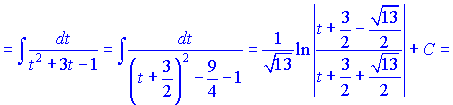
Вкінці не забуваємо замінити параметр t на тангенс половини кута
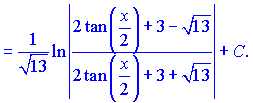
На вигляд інтегрування складне, проте і завдання не з простих. Іншої методики, яка б дозволяла аналітично знайти інтеграл Ви не знайдете, тож вивчайте і застосовуйте подану схему.
б)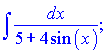 
Розв'язок. До даного прикладу застосовуємо попередні заміни
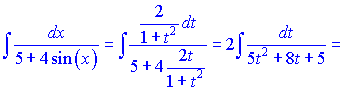
Це дозволить отримати в знаменнику дробу квадратичну функцію від параметра t. Далі її зводимо до суми квадратів
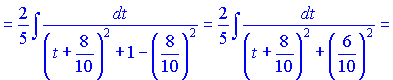
а це вже нам дає табличну формулу арктангенса
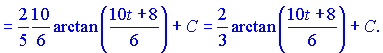
Ну і на останок замість t підставте тангенс половини кута, а то ми так захопилися обчисленнями, що забуи це зробити.
в)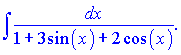 
Розв'язок. Застосовуємо універсальну заміну
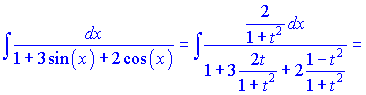
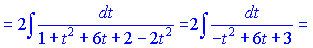
Трионометрична фунція в знаменнику зведеться до квадратичного тричлена, який записуємо у вигляді різниці квадратів
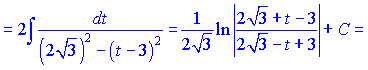
Подальше інтегрування дасть огарифм частки функцій. Остаточну відповідь записуємо після заміни параметра на тангенс половини кута
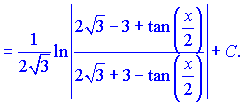
Інтегрування раціональних функцій від sin(x), cos(x) досить складне на практиці, тому слід бити уважними при спрощенні підінтегральної функції, а також при самому інтегруванні. Найменша помилка може призвести до неправильного результату, не поспішайте при обчисленні подібних інтегралів.
