Знайти радіус основи циліндра

Сьогодні розберемо тестові задачі із ЗНО курсу підготовки на знаходження радіуса основи циліндра. Завдання дещо складніші ніж шкільні, тому тут не будемо зупинятися на прикладах де відомо об'єм циліндра і висоту, а потрібно знайти радіус основи чи їм подібних. В завданнях слід виконати нескладну побудову і вже за нею визначити радіус. Для збільшення наведеного тут списку завдань просимо Вас надсилати нам тематично подібні відповіді до задач на циліндр.

38.4 Радіус циліндра

Задача 38.3 Діагональ осьового перерізу циліндра дорівнює l і утворює з площиною основи кут alpha.
Визначити радіус циліндра.

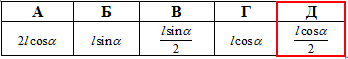
Розв'язання: Осьовим перерізом циліндра є прямокутник AA₁B₁B (див рис.).
Сторони AA₁=BB₁ є твірними циліндра (їх довжина дорівнює висоті H ), а інші дві сторони AB=A₁B₁ – діаметри основ циліндра.
Вісь циліндра OO₁ є віссю прямокутника, його кінці ділять діаметр навпіл, тобто AO=OB=A₁O=OB₁=R, де R – радіус циліндра.
Діагональ AB₁ прямокутника AA₁B₁B (за властивістю) ділить його на два рівних прямокутних трикутники ΔABB₁ і ΔAA₁B₁.

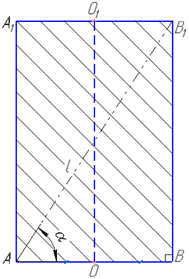
Ортогональною проекцією діагоналі AB₁ осьового перерізу AA₁B₁B є діаметр AB (або A₁B₁) основи циліндра.
Тому кут між діагоналлю AB1 і площиною основи є кут B₁AB (або кут AB₁A₁), отже ∠B₁AB=alpha.
Розглянемо прямокутний ΔABB₁ (∠ABB₁=90), у якого AB₁=l – гіпотенуза (за умовою задачі) і ∠B₁AB=alpha – кут, що є прилеглим до катета AB.
Із означенням косинуса гострого кута прямокутного трикутника виразимо катет AB:

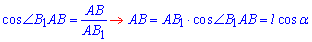
Далі знаходимо радіус циліндра як половину катета AO=OB=AB/2, тобто

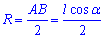
Відповідь: 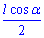– Д.

Задача 38.4 У циліндрі паралельно до його осі проведено площину на відстані 3 см від неї.
Ця площина перетинає основу циліндра по хорді, яка дорівнює 8 см. Знайти радіус циліндра.

Розв'язання: Переріз циліндра площиною, яка проходить паралельно осі циліндра є прямокутник AA₁B₁B, сторони AA₁=BB₁ якого є твірними циліндра (їх довжина дорівнює висоті H циліндра), а інші дві сторони AB=A₁B₁ – хорди основ циліндра, тобто AB=A₁B₁=8 см.
З центра основи циліндра O₁ опустимо перпендикуляр O₁M₁ на хорду A₁B₁, тобто O₁M₁⊥A₁B₁.
Оскільки твірні циліндра перпендикулярні до площин основи, а основи циліндра – два рівні круги, що лежать в паралельних площинах, то звідси O₁M₁=3 см – відстань від осі циліндра OO₁ до площини AA₁B₁ (прямокутника AA₁B₁B).
З центра основи O₁ проведемо відрізки A₁O₁ і B₁O₁.
Оскільки A₁B₁ – хорда основи, то A₁O₁ і B₁O₁ – радіуси основи, тому A₁O₁=B₁O₁=R.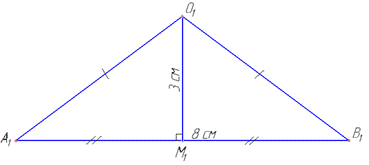

Звідси слідує, що ΔA₁O₁B₁ – рівнобедрений з основою A₁B₁=8 см і бічними сторонами A₁O₁=B₁O₁=R.
Відрізок O₁M₁=3 см – медіана, висота і бісектриса рівнобедреного ΔA₁O₁B₁ (за властивістю), тому A₁M₁=M₁B₁=A₁B₁/2=4 см і ∠A₁M₁O₁=∠B₁M₁O=90.
Із прямокутного трикутника A₁M₁O₁ (∠A₁M₁O=90), в якому A₁M₁=4 см і O₁M₁=3 см – катети,
за теоремою Піфагора знайдемо гіпотенузу A₁O₁=R – радіус циліндра:

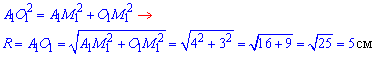
Відповідь: 5 см – Б.

Задача 38.6 Діагональ розгортки бічної поверхні циліндра дорівнює d й утворює з висотою розгортки кут alpha.
Знайти радіус циліндра.

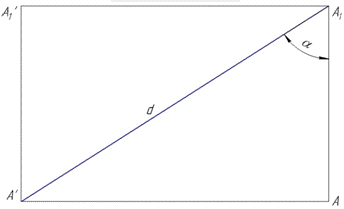
Розв'язання: Розгорткою бічної поверхні циліндра є прямокутник AA₁A₁'A', дві сторони AA₁ і A₁'A' якого є твірними (висотою) циліндра, а дві інші AA' і A₁A₁' є довжинами кіл – нижньої і верхньої основи циліндра відповідно, причому .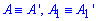
(Тут і надалі знак «», означає, що точки (або інші елементи) співпадають, накладаються).
Діагональ A'A₁ прямокутника AA₁A₁'A' ділить його на два рівних прямокутних трикутники (за властивістю).
За умовою задачі діагональ A'A₁ утворює з висотою розгортки кут alpha, тобто ∠AA₁A'=alpha.
Розглянемо прямокутний ΔAA1A' (∠A'AA1=90), у якого A'A1=d – гіпотенуза (за умовою задачі) і (∠AA1A'=alpha – кут, що є протилежним до катета AA'.
За означенням синуса гострого кута прямокутного трикутника знайдемо катет AA' – довжину кола:

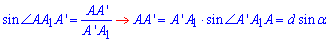
Отже, C=d•sin(alpha) – довжина кола, звідси
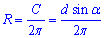– радіус кола,
де 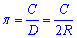– відношення довжини кола C до його діаметра D=2R.
Отже, 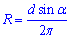– радіус кола.
Відповідь: 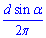– Б.

Задача 38.17 Знайти радіус циліндра, описаного навколо прямокутного паралелепіпеда зі сторонами 9 см і 12 см і висотою 8 см.

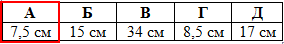
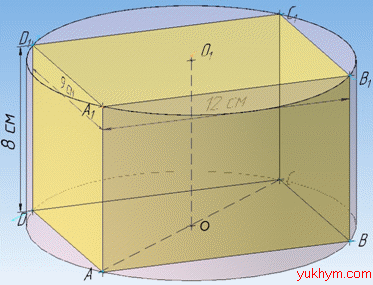
Розв'язання: Циліндр описаний навколо призми (циліндр описаний навколо прямокутного паралелепіпеда за умовою), якщо основи циліндра описані навколо основ призми (коло описане навколо прямокутника), а висота циліндра дорівнює висоті призми, тобто H=8 см.
Маємо прямокутний паралелепіпед ABCDA₁B₁C₁D₁, в основі якого лежить прямокутник ABCD зі сторонами AB=CD=12 см і AD=BC=9 см .

У прямокутника, за властивістю, діагоналі рівні і в точці перетину O діляться навпіл. Діагональ AC прямокутника ABCD знайдемо із прямокутного ΔABC (∠ABC=90) за теоремою Піфагора (AB=12 см і BC=9 см – катети):
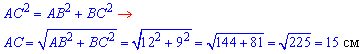Коло описане навколо прямокутника, якщо всі вершини прямокутника лежать на колі, а центр кола лежить на перетині діагоналей прямокутника. Тому діаметр кола дорівнює діагоналі AC вписаного прямокутника ABCD, а радіус R дорівнює половині діаметра (тобто половині діагоналі AC), отже R=AC/2=15/2=7,5 см – радіус (основи) циліндра.
Відповідь: 7,5 см – А.

Далі розглянемо приклади на обчислення площі осьового та під кутом перерізів циліндра. Їх теж отримано із посібника для ЗНО підготовки.
Щоб мати можливість вчитися з більшого різноманіття прикладів просимо Вас співпрацювати та ділитися навчальними матеріалами.