Задачі на кути в цилідрі

На попередніх уроках проаналізовано чимало завдань, де в умові були задані певні кути між лініями в циліндрі і потрібно було знайти висоту, радіус основи чи площу поверхні. Туи з точністю до навпаки: мінімум даних відомий, залишається знайти певний кут між лініями в циліндрі.

38.7 Циліндр. Задачі на кути

Задача 38.24 Площа основи циліндра відноситься до площі осьового перерізу як √3Pi:4.
Знайти у градусах кут між діагоналлю осьового перерізу циліндра і площиною основи.
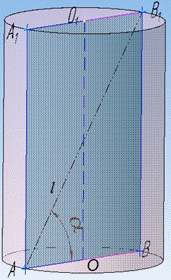
осьовий переріз циліндра
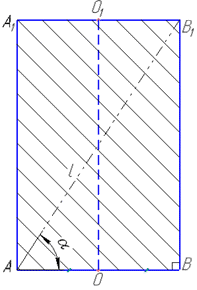
Розв'язання: Маємо циліндр з осьовим перерізом AA₁B₁B.
Площа основи циліндра:
S_oc=πR², де R – радіус основи циліндра;
Площа осьового перерізу – прямокутника AA₁B_1,/B:
S_пер=AB•AA₁=2R•H, де H – висота циліндра, AB=D=2R – діаметр циліндра.
За умовою задачі маємо
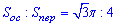, тобто 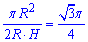, звідси отримаєм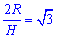о , або .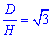
Оскільки осьовий переріз перпендикулярний до площини основи циліндра (звідси BB1⊥AB), проходить через його вісь (за означенням), то кут alpha – кут між діагоналлю AB1 перерізу і площиною основи циліндра (діаметр основи AB є ортогональною проекцією діагоналі AB₁ осьового перерізу A₁B₁B).
Розглянемо прямокутний трикутник ABB₁ (∠ABB₁=90), у якого AB=D – прилеглий катет (діаметр циліндра), а BB₁=H – протилежний катет (висота циліндра) до ∠BAB₁=alpha.
За означенням тангенса гострого кута прямокутного трикутника знайдемо кут alpha (нагадаємо, що 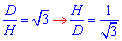, тоді):

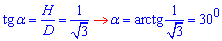
Отже, alpha=30 – кут між діагоналлю осьового перерізу і площиною основи циліндра, якщо відношення їх площ

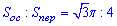
Відповідь: 30⁰.

Задача 38.25 Висота циліндра дорівнює 12, а радіус основи дорівнює 10. Циліндр перетнуто площиною, паралельно до його осі так, що в перерізі утворився квадрат. Знайти відстань від осі циліндра до січної площини.

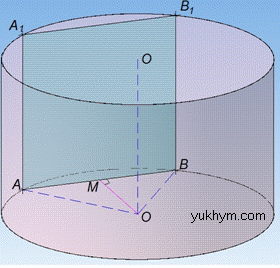
Розв'язання: Маємо циліндр з радіусом основи R=10 і висотою H=12. Маємо переріз циліндра, який проходить паралельно осі OO₁ циліндра (за умовою задачі), а значить перпендикулярний до площини основи (за властивістю). Звідси слідує, що AA₁=BB₁=12 – висота циліндра, а значить AB=12, оскільки AA₁B₁B – квадрат.
Проведемо перпендикуляр OM до площини перерізу (OM⊥AB).
Оскільки переріз AA₁B₁B перпендикулярний до площини основи, то відрізок OM – відстань від осі циліндра OO₁ до січної площини AA₁B₁B.
Проведемо відрізки AO і BO. Оскільки точки A і B належать основі циліндра (як точки перетину січної площини з основою циліндра), то AO=BO=R=10 – радіуси основи.
Звідси слідує, що трикутник AOB – рівнобедрений з основою AB=12.
Тоді за властивістю:
OM – висота, медіана і бісектриса проведені до основи AB. Звідси, AM=BM=AB/2=12/2=6. Із прямокутного трикутника AOM(∠AMO=90), у якого AO=10 – гіпотенуза, AM=6 – катет, за теоремою Піфагора знайдемо катет OM:

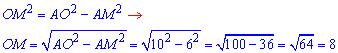
Отже, OM=8 – відстань від осі циліндра до січної площини.
Відповідь: 8.

Задача 38.33 У циліндрі проведено два перерізи ABCD і ABEF, де AB – твірна циліндра.
Площа кожного з цих перерізів дорівнює 0,5 площі осьового перерізу.
Знайти у градусах кут між площинами ABC і ABE.
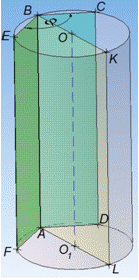
переріз циліндра
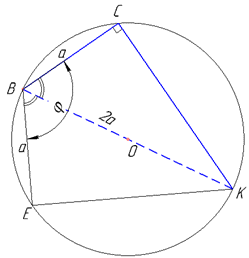
Розв'язання: Маємо циліндр з перерізами ABCD і ABEF. Оскільки AB – твірна (за умовою задачі), то перерізи ABCD і ABEF є прямокутниками і проведені паралельно до осі OO1 циліндра. Тобто площини ABC і ABE перпендикулярні до площини основи, тому кут між ними – це кут phi між відрізками BC і BE, які є проекціями відповідних площин на площину основи циліндра (круг з центром O). Отже phi=∠CBE – кут між площинами (перерізами ABCD і ABEF).
Маємо осьовий переріз циліндра – прямокутник ABKL зі сторонами AB=KL=H (висота) і AL=BK=2a (діаметр циліндра), який проходить через вісь OO1 циліндра. Площа осьового перерізу:
S_ABKL=AL•AB=2aH.
За умовою задачі площі перерізів ABCD і ABEF становлять 0,5 площі осьового перерізу, тому 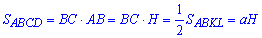, звідси отримаємо BC=a;
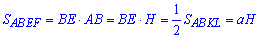, звідси отримаємо BE=a.
На площині основи циліндра проведемо відрізки CK і EK.
Отримали кути вписані у коло ∠BCK і ∠BEK відповідно, які спираються на діаметр BK. За властивістю кутів вписаних у коло (кути, які спираються на діаметр – прямі) ∠BCK=∠BEK=90, а тому прямокутні ΔBCK і ΔBEK – рівні за гіпотенузою (BK=2a спільна) і катетом BC=BE=a. Звідси ∠KBC=∠KBE=phi/2.
Розглянемо прямокутний трикутник BCK (∠BCK=90), у якого BC=a – прилеглий катет до ∠KBC=phi/2 і BK=2a – гіпотенуза. За означенням косинуса гострого кута прямокутного трикутника знайдемо ∠KBC=PHI/2:

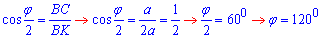
Відповідь: 120⁰.

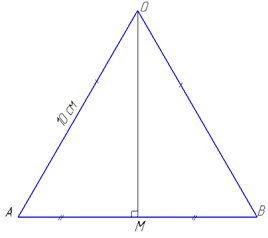
Задача 38.1 Д У рівносторонньому циліндрі радіус основи дорівнює 5√6. Точку кола верхньої основи сполучили з точкою кола нижньої основи. Проведена пряма утворює з площиною основи кут 60.
Визначити відстань від цієї прямої до осі циліндра.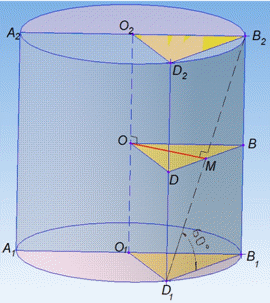
циліндр, ЗНО
Розв'язання: Маємо циліндр з висотою O₁O₂=H і радіусом основи R=5√6.
Рівносторонній циліндр – це той циліндр, осьовим перерізом якого є квадрат, тобто діаметр основи D=2R дорівнює висоті H, отже, H=D=2R=10√6.
Проведемо відрізок B₂D₁, який сполучає точку кола верхньої основи циліндра B₂ з точкою кола нижньої основи D₁.
Оскільки B₁B₂=H – висота циліндра, то B₁B₂ – перпендикуляр на площину нижньої основи циліндра, B₂D₁ – похила, тоді B₁D₁ – проекція похилої на площину нижньої основи, звідси ∠B₁D₁B₂=60 – кут між прямою B₂D₁ і площиною основи циліндра.
Побудуємо трикутну призму O₁B₁D₁O₂B₂D₂, у якої основи є рівнобедрені трикутники O₁B₁D₁ і O₂B₂D₂ з основою B₁D₁, B₂D₂ і бічними сторонами O₁B₁=O₁D₁=R=5√6, O₂B₂=O₂D₂=5√6 відповідно.
Тоді відрізок B2D1 – діагональ грані B₁D₁D₂B₂.
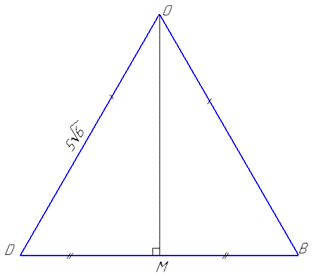
Через середину висоти призми (циліндра) B₁B₂=H паралельно основам призми проведемо переріз OBD, який буде рівним трикутникам O₁B₁D₁ і O₂B₂D₂, тому OB=OD=R=5√6 і BD=B1D1.
Висота OM трикутника OBD є відстанню від осі циліндра до грані B₁D₁D₂B₂, тобто до прямої B₂D₁, так як OM – спільний перпендикуляр для прямих O₁O₂ і B₂D₁.
(Перерізи проведені паралельно основам призми є перпендикулярними до висоти призми O₁O₂ і бічних граней).
Із прямокутного трикутника B₁D₁B₂ (∠B₂B₁D₁=90), у якого B₁B₂=H=10√6 – протилежний катет до кута ∠B₁D₁B₂=60 за означенням тангенса гострого кута прямокутного трикутника знайдемо прилеглий катет B1D1:
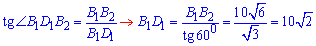
тангенс кута
отже BD=B₁D₁=10√2.
Так як трикутник OBD – рівнобедрений (OB=OD=R=5√6), то за властивістю OM⊥BD і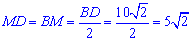
Із прямокутного ΔOMD (∠OMD=90), у якого MD=5√2 – катет і OD=R=5√6 – гіпотенуза, знайдемо катет OM за теоремою Піфагора – відстань від осі циліндра до прямої B₂D₁:

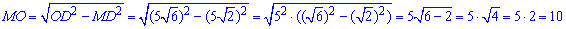
Відповідь: 10.