Проаналізуємо відповіді до задач на комбінацію циліндра і призми. До них віднесемо випадки коли циліндр вписаний у призму (трикутну чи чотирикутну), і навпаки - коли призма вписана в циліндр. Таких задач у нас поки що небагато, тому Вас просимо бути активними і надсилати нам задачі, які тут не було охоплено. Наведені далі завдання відповідають програмі з підготовки до ЗНО тестування.
38.3 Циліндр вписаний у призму
Задача 38.18 Об'єм правильної трикутної призми дорівнює V.
Визначити об'єм циліндра, вписаного в призму.
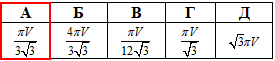
Розв'язання: Об'єм циліндра обчислюють за формулою:
V=Soc•H=πR2H,
де Soc=πR2 – площа основи циліндра (площа круга);
H – висота циліндра.
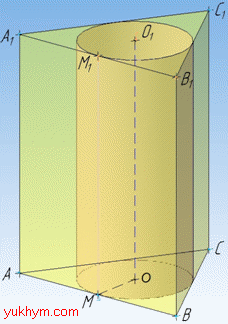
Циліндр вписаний у призму, якщо основи циліндра вписані в основу призми, а висота циліндра дорівнює висоті призми.
Маємо правильну трикутну призму ABCA1B1C1 з об'ємом V, в основі якої лежить правильний (рівносторонній) трикутник ABC.
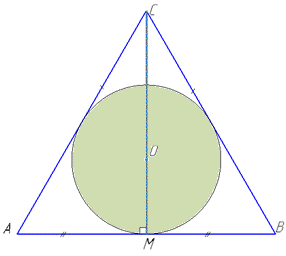
Нехай довжина сторони трикутника дорівнює a. Тоді площа основи трикутної призми (площа ΔABC) рівна:
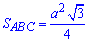
Формула об'єму трикутної призми:
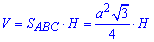
звідси отримаємо залежність
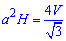
Коло вписано в трикутник, якщо всі сторони трикутника дотикаються до кола.
Радіус вписаного кола в правильний трикутник:
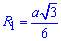– радіус І циліндра.
Знаходимо об'єм І циліндра:
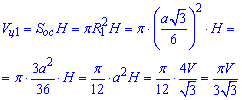
Тут підставили залежність, отриману з об'єму трикутної призми.
Відповідь: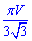 
– А.
Задача 38.19 У циліндр вписано правильну трикутну призму, а у призму – циліндр. Знайдіть відношення об'ємів циліндрів.
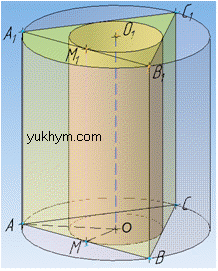
Розв'язання: З попередньої задачі 38.18 встановили, що об'єм (І) циліндра, вписаного в правильну трикутну призму дорівнює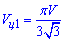 
Циліндр (ІІ) описаний навколо призми, якщо основи циліндра описані навколо основ призми, а висота циліндра дорівнює висоті призми. Коло описане навколо трикутника, якщо всі вершини трикутника лежать на колі.
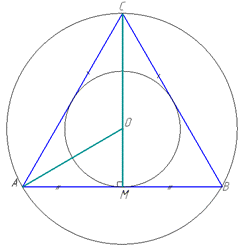
Радіус описаного кола навколо правильного трикутника зі стороною a:
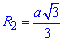– радіус ІІ циліндра.
Об'єм ІІ циліндра:
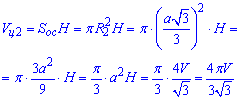
Складемо відношення об'ємів вписаного (І) і описаного (ІІ) циліндрів:
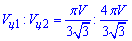
звідси слідує, що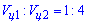 
(Відношення об'ємів вписаного і описаного циліндрів було встановлено через об'єм призми V, але в умові задачі 38.19 цього не дано.)
Тому покажемо Вам ще один спосіб розв'язку задачі:
оскільки висоти призми і обох циліндрів рівні, то достатньо скласти відношення площ основ циліндрів (як подібних фігур), які виражаються через радіуси вписаного і описаного кіл відповідно, тобто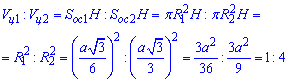 
Відповідь: 1: 4 – Б.
Задача 38.23 Установити відповідність між об'ємами правильних трикутних призм (1–4) та об'ємами вписаних у них циліндрів (А–Д).
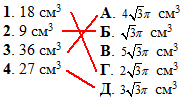
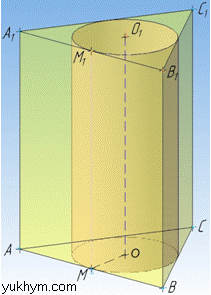
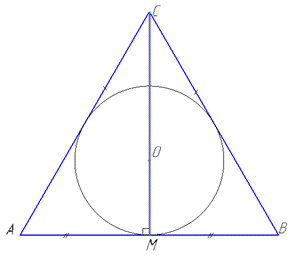
Розв'язання: (Розв'язок цієї задачі дивись у номері 38.18.)
Обчислимо об'єм циліндра за попередньо виведеною формулою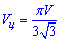 
для запропонованих тестових варііантів:
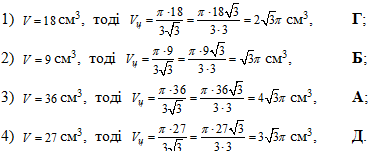
Задача 38.32 Основою прямої призми є рівнобічна трапеція, основи якої дорівнюють 8 і 2. Висота призми дорівнює 10/π. Знайти об'єм циліндра, вписаного в цю призму.
Розв'язання: Об'єм циліндра обчислюють за формулою:
V=SocH=πR2•H, де Soc=πR2 – площа основи циліндра (площа круга); H – висота циліндра.
Циліндр вписаний у призму, якщо основи циліндра вписані в основу призми, а висота циліндра дорівнює висоті призми
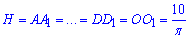
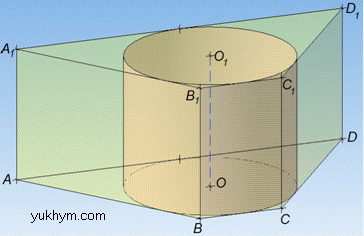
Маємо пряму призму ABCDA1B1C1D1, в основі якої лежить рівнобічна трапеція з основами BC=2, AD=8 і бічними сторонами AB=CD.
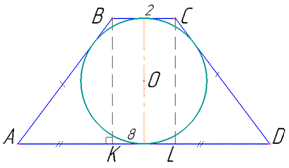
Коло вписано в трапецію, якщо всі сторони трапеції дотикаються до кола. За властивістю чотирикутника описаного навколо кола – суми довжин його протилежних сторін рівні – маємо
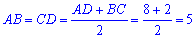
Оскільки основи трапеції дотикаються до вписаного в неї кола, то висота трапеції BK (або CL) є діаметром вписаного кола.
Знайдемо висоту трапеції BK.
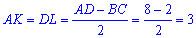
(за властивістю рівнобічної трапеції).
Із прямокутного трикутника ABK (∠AKB=90, оскільки BK⊥AD, AB=5 – гіпотенуза і AK=3 – катет) знайдемо катет BK.
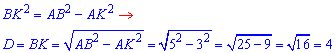
Отже, D=4 – діаметр вписаного кола (основи циліндра), R=D/2=2 – радіус основи вписаного циліндра.
Обчислюємо об'єм циліндра:
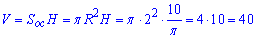
Відповідь: 40.
Задача 38.31 У циліндр вписано призму, основою якої є прямокутний трикутник з катетом 1 і прилеглим до нього кутом 600. Визначити об'єм циліндра, якщо висота призми дорівнює 1/π.
Розв'язання: Об'єм циліндра знаходимо за формулою:
V=SocH=πR2H,
де Soc=πR2 – площа основи циліндра (площа круга);
H – висота циліндра.
Циліндр описаний навколо призми (трикутної призми за умовою), якщо основи циліндра описані навколо основ призми (коло описане навколо трикутника), а висота циліндра дорівнює висоті призми
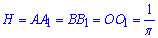
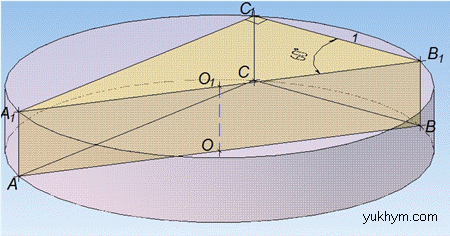
Маємо трикутну призму, в основі якої лежить прямокутний трикутник ABC (∠ACB=90) з катетом BC=1 і прилеглим до нього кутом ∠ABC=60.
За означенням косинуса гострого кута прямокутного трикутника знайдемо гіпотенузу AB:
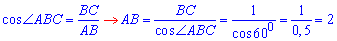
Коло описане навколо прямокутного трикутника, якщо всі вершини трикутника лежать на колі, а центр кола лежить на гіпотенузі прямокутного трикутника і (за властивістю) ділить її навпіл. Тому діаметр кола дорівнює гіпотенузі AB=2 вписаного прямокутного ΔABC, а радіус R дорівнює половині діаметра:
R=AB/2=1 – радіус основи циліндра.
Знаходимо об'єм циліндра:
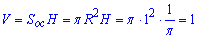
Відповідь: 1.
Далі йдуть задачі на радіус та висоту циліндра.
