Формула для обчислення довжини кола за відомим радіусом R або діаметром D доволі проста
C=πD=2πR.
Але завдань коли можемо напряму застосувати цю формулу мало як в шкільній практиці так і у ВУЗах. Далі зібрано частину із 35 прикладів для ЗНО підготовки, в яких в умові завдання потрібно знайти довжину кола. Спершу йдуть легші тестові завдання де Вам дають вибрати один із 5 варіантів відповідей, далі складніші завдання де потрібно обґрунтувати як Ви прийшли до результату. Уважно аналізуйте відповіді та вивчайте наведені в розрахунках формули.
Задача 34.1
А | Б | В | Г | Д |
10π см | 40π см | 20π см | 100π см | 50π см |
Розв'язання: До перших двох завдань можна побудувати наступний схематичний рисунок
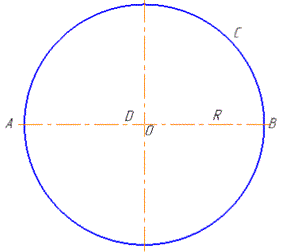
Формула для обчислення довжини кола:
C=πD=2πR, де C - довжина кола;
AB=D=2R - діаметр кола;
OA=OB=R - радіус кола;
π≈3,14 - відношення довжини кола до його діаметра;
таким чином маємо за умовою D=20 см, звідси
C=Dπ=20π см.
Відповідь: 20π см – В.
Задача 34.3 Знайти довжину дуги кола, радіус якого дорівнює 10 см, якщо її кутова величина дорівнює 300.
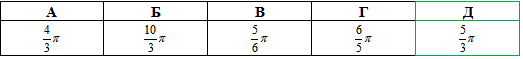
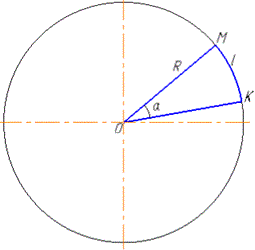
Розв'язання: Запишемо формулу для обчислення довжини дуги кола:
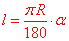
де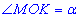 
- градусна міра відповідного центрального кута;
OM=OK=R - радіус кола.
π≈3,14 - відношення довжини кола до його діаметра;
l - довжина дуги кола,
Підставляємо дані з умови R=10 см, alpha=30 в формулу та обчислюємо
Отримане значення відповідає варіанту Д тестових відповідей.
Відповідь: 5π/3 – Д.
Задача 34.10 При збільшенні круга його площа збільшилася у 9 разів. У скільки разів збільшилась довжина кола цього круга?
А | Б | В | Г | Д |
1,5 | 27 | 9 | 2 | 3 |
Розв'язання: Відношення площ кругів S1/S2 дорівнює відношенню квадратів їх лінійних розмірів, зокрема і відношенню квадратів довжин їхніх кіл
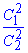, тобто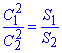
де відношення площ рівне 9 за умовою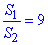 
, звідси знаходимо коефіцієнт пропорційності
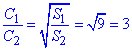
Відповідь: 3 – Д.
Задача 34.11 З точки кола проведено дві перпендикулярні хорди, довжини яких дорівнюють 12 і 16. Знайти довжину кола.
А | Б | В | Г | Д |
20π см2 | 40π см2 | 50π см2 | 60π см2 | 35π см2 |
Розв'язання: Побудуємо рисунок до задачі. Маємо коло з центром у точці O, дві хорди AC=16 см і BC=12 см (∠ACB=90 за умовою).
Оскільки ∠ACB - прямий, то він спирається на діаметр AB.
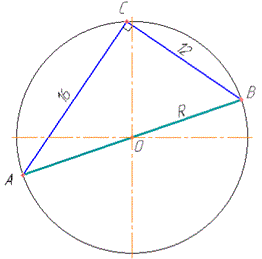
Із прямокутного ΔACB за теоремою Піфагора знайдемо гіпотенузу AB:
AB2=AC2+BC2, беремо корінь квадратний з обох частин від знаку рівності
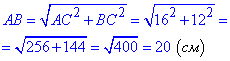
Отже, D=AB=20 (см) - діаметр заданого кола.
C=πD=20π (см) - довжина заданого кола.
Відповідь: 20π – А.
Задача 34.25 У рівнобедрену трапецію вписано коло. Основи трапеції дорівнюють 9 і 25.
Знайти: 1) бічну сторону;
2) довжину l вписаного кола. У відповідь записати l/π.
Розв'язання: Нехай маємо рівнобедрену трапецію ABCD, AD||BC, AB=CD - бічні сторони і BC=9, AD=25 – основи трапеції.
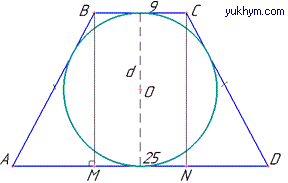
У трапецію ABCD вписано коло з центром у точці O.
Тому, за властивістю вписаного кола у чотирикутник, суми протилежних сторін чотирикутника рівні, тобто AB+CD=AD+BC, звідси знайдемо бічну сторону рівнобедреної трапеції ABCD:
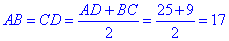
Оскільки коло вписане у трапецію, то радіус перпендикулярний до сторін трапеції (в точках дотику), тому діаметр вписаного кола дорівнює висоті трапеції.
Проведемо висоти BM і CN трапеції ABCD.
Оскільки BM=CN, AB=CD, BM⊥AD і CN⊥AD, то (за ознакою рівності прямокутних трикутників) ΔAMB=ΔDNC, звідси слідує, що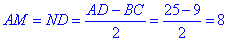 
(Тут MN=BC=9).
У прямокутному трикутнику ΔAMB (∠AMB=90) за теоремою Піфагора знайдемо катет BM - висоту рівнобедреної трапеції ABCD:
BM2=AB2-AM2, звідси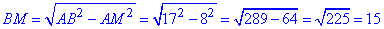 
Отже, d=BM=15 - діаметр вписаного кола.
Знайдемо довжину вписаного кола l:
l=dπ=15 π.
Звідси, l/π =15.
Відповідь: 1) 17, 2) 15.
Задача 34.24 Знайти довжину кола l, вписаного в ромб, діагоналі якого дорівнюють 15 і 20. У відповідь записати l/π.
Розв'язання: Нехай маємо ромб ABCD, AC=15 і BD=20 - діагоналі ромба.
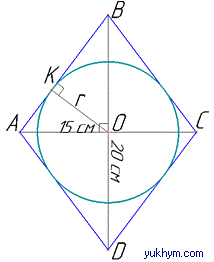
У ромб ABCD вписано коло з центром у точці O - точка перетину діагоналей ромба і дотикається до сторони AB у точці K.
Тому OK=r - радіус вписаного кола і, за властивістю, AB⊥OK.
А за властивістю діагоналей ромба (діагоналі ромба перпендикулярні і в точці перетину діляться навпіл):
AC⊥BD і AO=CO=AC/2=7,5, BO=DO=BD/2=10.
Отже, OK - висота прямокутного трикутника ΔAOB.
У прямокутному ΔAOB (∠AOB=90) за теоремою Піфагора обчислимо гіпотенузу AB:
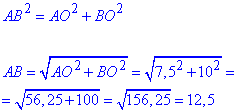
Знайдемо площу прямокутного трикутника ΔAOB через півдобуток катетів:
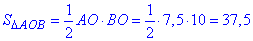
Знайдемо висоту OK прямокутного ΔAOB - радіус вписаного кола r у ромб ABCD:
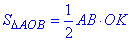, звідси
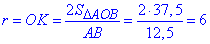
ІІ – спосіб:
Знайдемо площу ромба ABCD:
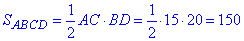
Обчислимо півпериметр ромба ABCD (у ромба всі сторони рівні):
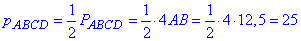
Знайдемо радіус вписаного кола r у ромб ABCD:
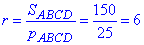
Знайдемо довжину вписаного кола l:
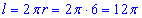
Отже, l/π =12.
Відповідь: 12.
Задача 34.26 Периметр правильного трикутника дорівнює 36. На стороні трикутника, як на діаметрі, побудовано коло.
Знайти довжину l дуги, розміщену у внутрішній області трикутника. У відповідь записати l/π.
Розв'язання: Нехай маємо правильний трикутник ABC з периметром PΔABC=36.
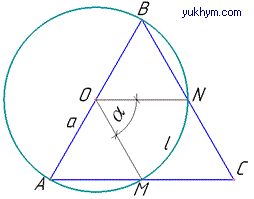
Тоді сторона правильного ΔABC (у правильного трикутника всі сторони рівні):
a= PΔABC:3=36:3=12.
На стороні AB=a цього трикутника, як на діаметрі, побудовано коло з центром у точці O (за умовою), тому R=AO=BO=a:2=6 - радіус цього кола.
Це коло перетинає сторони AC і BC трикутника ABC у точках M і N, відповідно.
OMі ON. Оскільки AO=BO=OM=ON=R і ∠OAM=∠OBN=60 (як внутрішні кути правильного трикутника ΔABC), то звідси впливає (якщо у рівнобедреного трикутника хоча б один кут дорівнює 600, то він є правильним), що ∠MON=alpha=60 - центральний кут, що стягує дугу 
у внутрішній області ΔABC, довжину l якої треба знайти.
Знайдемо довжину дуги l, розміщену у внутрішній області ΔABC - довжину дуги сектора з центральним кутом alpha=60:
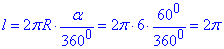
Отже, l/π=2.
Відповідь: 2.
Решта задач стосуються обчислення лінійних розмірів кола, визначення центрального та внутрішніх кутів в колі та обчислення площ як круга так і складних фгур, отриманих на його основі.
