Задачі на трикутник бувають прості, складні і дуже складні. Якщо маємо прямокутний трикутник то формули для обчислення площі, катетів, радіусів вписаного та описаного кіл дещо спрощуються. Нижче наведені розв'язки прикладів на будь-який смак, аналізуйте їх – можливо вони допоможуть Вам в навчанні.
Задача 1. Знайдіть гіпотенузу і синуси гострих кутів прямокутного трикутника, якщо його катети дорівнюють: а) 6см і 8см; б) 4см і 7см.
Розв'язок. Застосуємо теорему Піфагора до заданих катетів
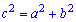
Для завдання а) гіпотенуза рівна

та для б) відповідно
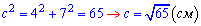
Синус гострого кута в прямокутному трикутнику рівний відношенню катета навпроти кута до гіпотенузи.
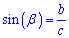
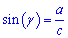 .
.
Рисунок з необхідними формулами для синусів та формулою Піфагора наведено нижче
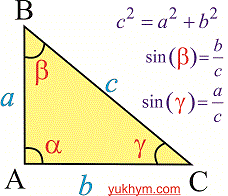
Обчислюємо синуси шуканих кутів
а) 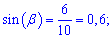
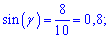
б)
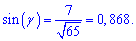
На цьому приклад розв'язано.
Приклад 1. Як визначити площу трикутника за катетом та гіпотенузою?
Розв'язування:Використаємо рисунок з попереднього завдання. Нехай відомо катет a і гіпотенузу c.
За теоремою Піфагора знаходимо другий катет прямокутного трикутника
b=√(c2-a2) .
Площа трикутника рівна півдобутку основи на висоту, для прямокутного трикутника це може бути півдобуток катетів, так як між ними прямий кут.
Тому площа дорівнює
S=a•√(c2-a2)/2.
По аналогії, якщо задано інший катет і Вам не хочеться вертіти позначеннями, то площа рівна
S=b•√(c2-b2)/2.
Відповідь:S=a•√(c2-a2)/2; S=b•√(c2-b2)/2.
Задача 2. Знайдіть катети прямокутного трикутника, якщо його гіпотенуза і другий катет відповідно рівні: а) 15см і 9см; б) 8см і 4см.
Розв'язок. На основі теореми Піфагора отримаємо
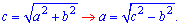
Підставляємо значення
а) 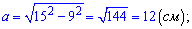
б) 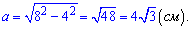
Відповідь: Катети трикутника рівні 12 см та  см.
см.
Задача 3. Гіпотенуза прямокутного трикутника дорівнює 17 см. Один з його катетів на 7 см менший від гіпотенузи. Знайдіть косинус меншого гострого кута.
Розв'язок. Для заданого завдання і подібних йому необхідно складати рівняння. В цьому прикладі позначимо через
x – більший катет, тоді
x-7 –менший катет.
За формулою Піфагора матимемо
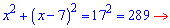
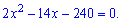
Ділимо на два та розв'язуємо квадратне рівняння з допомогою дискримінанту
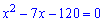
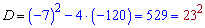
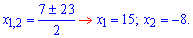
Другий корінь рівняння відкидаємо, оскільки він суперечить умові завдання. Таким чином один катет рівний 15 см, а другий – 15-7=8 см.
Відповідь: Катети прямокутного трикутника рівні 15 і 8 см.
Задача 4. Обчисліть довжину висоти рівностороннього трикутника, сторона якого дорівнює 12см.
Розв'язок. Якщо трикутник рівносторонній, то висота ділить основу навпіл. Крім цього висота є перпендикуляром. Таким чином завдання полягає в знаходженні катета коли відомо, що гіпотенуза рівна 12 см, а другий катет – 12/2=6 см.
За теоремою Піфагора обчислюємо
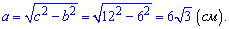
Відповідь: Катет рівний  см.
см.
Задача 5. Сторона квадрата рівна 7 см. Визначте довжину діагоналі.
Розв'язок. Оскільки сторони квадрата рівні, то потрібно знайти гіпотенузу прямокутного рівнобедреного трикутника з катетами довжиною 7 см. Використовуємо відому формулу Піфагора
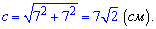
Відповідь: Діагональ квадрата рівна 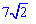 см.
см.
Задача 6. Більша діагональ і більша основа прямокутної трапеції дорівнюють відповідно 8 см і 6 см. Знайдіть довжину меншої бічної сторони трапеції.
Розв'язок. Розглянемо допоміжний рисунок, щоб було зрозуміло, що потрібно шукати.
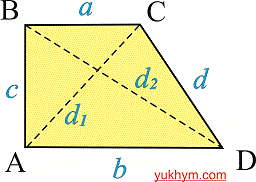
За умовою відома діагональ BD=8 см та AD=6 см. Катет AB прямокутного трикутника знаходимо за формулою
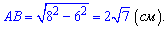
Відповідь: Сторона трапеції рівна 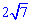 см.
см.
Задача 7. У трикутнику АВС кут В = 90 градусів, ВD перпендикулярна АС, АВ = 16см, ВС = 12см. Знайдіть довжину відрізка АD і тангенс кута при основі.
Розв'язок. Розглянемо допоміжний рисунок, щоб було зрозуміло, що потрібно шукати.
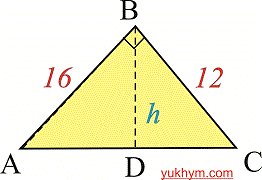
Складемо пропорції для відшукання відрізка AD
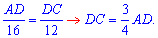
Друге рівняння побудуємо на основі теореми Піфагора
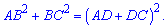
Думаю досі Вам усе зрозуміло. Наступним кроком підставляємо DC та значення катетів у рівняння
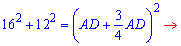
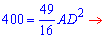
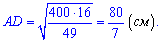
Відрізок знайдено, тангенс кута А знаходимо за формулою
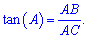
Визначимо довжину гіпотенузи, для цього знайдемо невідому частину DC
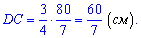
Гіпотенуза рівна сумі AD+DC
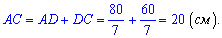
Обчислимо тангенс кута при основі
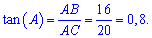
Відповідь: AD=80/7, tan(A)=0,8.
Задача 8. Периметр прямокутного трикутника дорівнює 12см, а один із з його катетів – 3см. Знайдіть площу трикутника.
Розв'язок. Даний приклад на складання рівняння з невідомими.
Перше рівняння відповідає формулі периметра трикутника, друге – теоремі Піфагора.
Позначимо b – невідомий катет, с – гіпотенуза трикутника.
Складаємо систему рівнянь
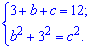
Маємо два рівняння з двома невідомими. Метод розв'язування Вам відомий з першого рівняння виражаємо одну із змінних і підставляємо в друге. В результаті після спрощень отримаємо квадратне рівняння один з коренів якого і буде розв'язком. Другий отримаємо в результаті підстановки в першу залежність системи рівнянь.
В мене вийшло, що b=4 см, c=5 см.
Якщо не вірите, то можете пройти описані вище процедури.
Площу знаходимо як половину добутку катетів
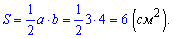
Відповідь: площа трикутника 6 сантиметрів квадратних.
Задача 9. Катети прямокутного трикутника рівні 3 см і 4 см. Знайти радіус вписаного та описаного кола.
Розв'язок. Радіус описаного кола знайти найлегше – він рівний половині гіпотенузи. Обчислюємо її довжину за теоремою Піфагора
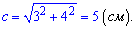
Звідси знаходимо більший радіус
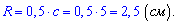
Радіус вписаного в прямокутний трикутник кола можна знайти декількома способами.
Підемо найпростішим і визначимо його на основі формули площі трикутника
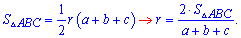
Як бачите обчислити радіус вписаного кола достатньо просто. Знаходимо площу трикутника
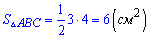
та підставляємо в попередню формулу
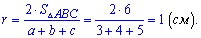
Ось такий складний на сприйняття приклад легко вирішується при знанні необхідних формул.
Відповідь: радіуси описаного та вписаного кіл рівні 2,5 см та 1 см відповідно.
Задача 10. Периметр прямокутного трикутника 60 см, а медіана що проведена до гіпотенузи рівна 13 см. Знайти площу трикутника.
Розв'язування: Використаємо одну з властивостей:
Медіана прямокутного трикутника рівна радіусу описаного кола, а гіпотенуза - діаметру цього кола.
Звідси гіпотенуза АВ=2*13=26 см.
P=АВ+ВС+АС=60 см.
Звідси
АВ+ВС=60-26=34 см.
Нехай АВ=х, тоді ВС=34-х.
За теоремою Піфагора
х²+(34-х)²=26²,
х²-34х+240=0,
D=b²-4ac=(-34)²-4•240=196=14²
x₁=(34+14)/2
х₂=(34-14)/2
х₁=24 см
х₂=10 см.
Звідси другий катет відповідно рівний
34-24=10 см
або
34-10=24 см.
Площа рівна півдобутку катетів:
S=10*24/2=120 см2.
Вивчайте формули основних геометричних фігур, набирайтеся досвіду на практиці і з часом приклади розв'язуватимете без труднощів. Якщо ж не вдається розв'язати приклад чи задачу, або незрозуміла умова завдання звертайтеся до спеціалістів. На цьому сайті та подібних інтернет ресурсах Ви завжди маєте можливість вирішити будь-яке складне завдання.


