Розглянемо кілька прикладів на знаходження повної поверхні конуса.
Повна поверхня рівна площі основи - круга та бічній площі. Бічна поверхня конуса знаходиться через розгортку на площину по твірній.
Розгортка бічної поверхні конуса є круговим сектором, радіус якого рівний твірній конуса, а довжина дуги сектора відповідає довжині основи кола.
Далі наведемо кілька готових розв'язків тестових задач із ЗНО підготовки на обчислення повної поверхні конуса.
Завдання підібрані різнопланові, тому на кількох прикладах охопимо ряд поширених задач на конуси за 10-11 класи.
Задача39.3 Знайти площу повної поверхні конуса, твірна якого дорівнює 10 см, а радіус основи дорівнює 6 см.
Розв'язання: Площа повної поверхні конуса обчислюється за формулою:
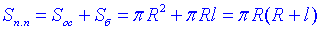
де R=AO=BO – радіус основи конуса;
l=SA=SB – твірна конуса.
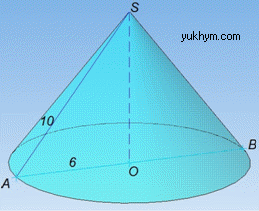
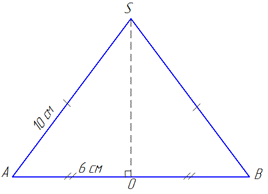
Маємо конус з твірною l=SA=SB=10 см і радіусом основи R=AO=BO=6 см (за умовою задачі).
Площа повної поверхні конуса:
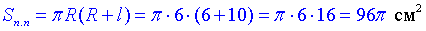
Тут застосували просту формулу площі поверхні, яку Ви не раз використовували на практичних заняттях в школі.
Відповідь: 96π см2 – Б.
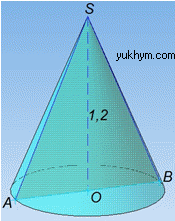
Задача 39.26 Площа осьового перерізу конуса дорівнює 0,6. Висота конуса дорівнює 1,2.
Обчислити площу S повної поверхні конуса. У відповідь записати S/π.
Розв'язання: Площа повної поверхні конуса обчислюється за формулою:
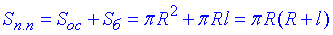, де R=AO=BO – радіус основи конуса;
l=SA=SB – твірна конуса.
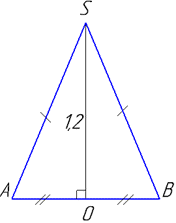
Маємо конус з висотою H=SO=1,2 і осьовим перерізом ΔSAB
(дивись І абзац задачі 39.1), площа якого S=0,6 (за умовою задачі).
Площа осьового перерізу – це площа трикутника:
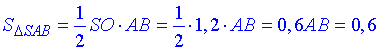
Звідси D=AB=1 – діаметр основи конуса, тоді R=AO=BO=D/2=0,5 – радіус основи.
Із прямокутного ΔSAO (∠AOS=90), у якого S=1,2 і AO=0,5 – катети, за теоремою Піфагора знайдемо гіпотенузу SA=l – твірну заданого конуса:
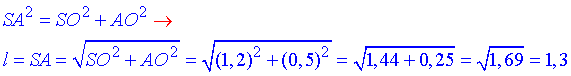
Отже, R=0,5 – радіус основи і l=1,3 – твірна заданого конуса.
Знаючи радіус і твірну, без проблем знаходимо площу повної поверхні конуса:
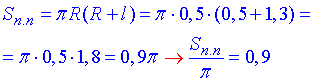
З наведеного вище бачимо, що в таких задач основна частина розрахунків припадає на вираження твірної або радіуса конусу.
Відповідь: 0,9.
Задача 39.28 Бічна поверхня конуса дорівнює 10 см2 і розгортається у сектор з кутом 36.
Знайти у квадратних сантиметрах повну поверхню конуса.
Розв'язання: Маємо конус з площею бічної поверхні Sb=10 см2, який розгортається у сектор з кутом 36.
Рисунок розгортки конуса має вигляд
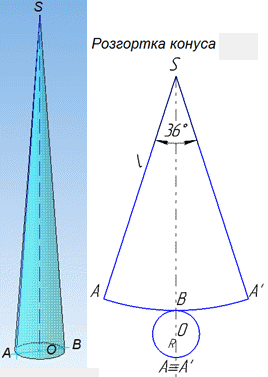
Площа сектора і є площею бічної поверхні конуса, та розраховується за формулою:
Sb=πRl, де l – твірна конуса;
площа основи конуса:
Soc=πR2, де R – радіус основи конуса;
площа сектора з кутом alpha0:
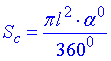
оскільки радіус сектора є твірною конуса.
З цієї формули знаходимо твірну
,
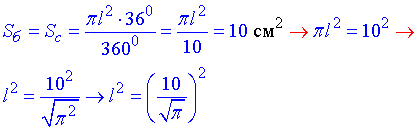тобто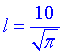 
см – довжина твірної заданого конуса.
Далі виражємо радіус основи
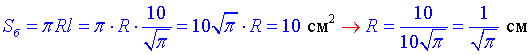
Площа основи конуса – круга рівна:
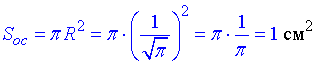
Площа повної поверхні конуса знаходимо сумуванням:
.
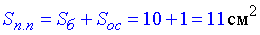Відповідь: 11.
Задача 39.31 Ромб, площа якого дорівнює Q, обертається навколо сторони.
Визначити площу S поверхні одержаного тіла. У відповідь записати S/(πQ).
Розв'язання: Маємо ромб ABCD, в якому SABCD=Q – площа;
нехай AB=BC=CD=AD=l – довжина сторони і AK=r – висота ромба ABCD.
Тоді площа ромба визначається через подвійну площу трикутників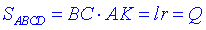 
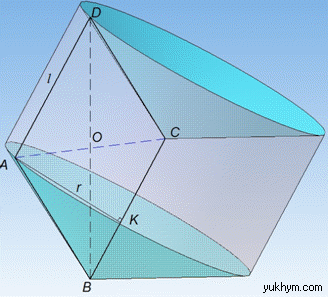
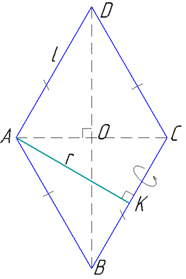
Тіло, яке утвориться при обертанні ромба ABCD навколо сторони (BC наприклад) складається з циліндра і двох конусів.
Оскільки BC – вісь обертання і AK⊥BC, то AB=l і CD=l – твірні конусів, а AK=r – радіус основи конусів.
Так як у ромба всі сторони і висоти проведені до них рівні, то два утворених конуси також рівні.
Площа поверхні (бічної) конуса:
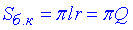
З тих же міркувань AK=r – радіус основи циліндра, оскільки основи конусів і циліндра співпадають;
AD=DC=l – твірні (або висота) циліндра.
Площа поверхні (бічної) циліндра:
Площа поверхні утвореного тіла обертання:
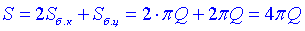
S/(πq)=4.
Відповідь: 4.
Задача 39.32 Рівнобічну трапецію, основи якої дорівнюють 8 і 18, обертають навколо більшої основи.
Знайти площу S поверхні тіла обертання, якщо відомо, що в цю трапецію можна вписати коло. У відповідь записати S/π.
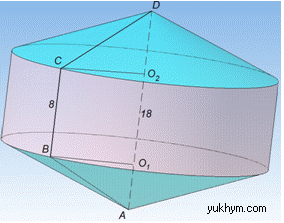
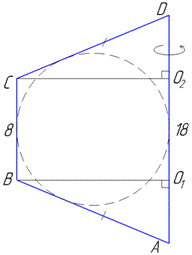
Розв'язання: Маємо рівнобічну трапецію ABCD, у якій BC=8 і AD=18 – основи;
AB=CD=(8+18)/2=13 – бічні сторони (їх обчислено за властивістю кола вписаного в чотирикутник, тобто суми протилежних сторін цього чотирикутника рівні).
Відрізки BO1 і CO2 – висоти трапеції ABCD, тому B1=CO2 і B1⊥AD, C2⊥AD.
Оскільки трапеція ABCD – рівнобічна, то AO1=DO2=(AD-BC)/2=(18-8)/2=5 (це випливає із рівності прямокутних ΔABO1 й ΔDC2).
Звідси за теоремою Піфагора у відповідних трикутників знайдемо висоти BO1 і CO2:
Отже, маємо AB=CD=13 – бічні сторони і BO1=CO2=12 – висоти трапеції ABCD.
Тіло, яке утвориться при обертанні рівнобічної трапеції ABCD навколо більшої основи AD складається з циліндра і двох конусів.
Оскільки AD – вісь обертання і BO1⊥AD, CO2⊥AD, то lk=AB=CD=13 – твірні конусів, а r=BO1=C2=12 – радіус основи конусів.
Так як трапеція ABCD – рівнобічна, то два утворених конуси рівні.
Площа поверхні (бічної) конуса:
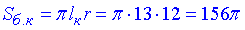
З тих же міркувань r=BO1=CO2=12 – радіус основ циліндра, оскільки основи конусів і циліндра співпадають;
lc=BC=O1O2=8 – твірні (або висота) циліндра.
Площа поверхні (бічної) циліндра:
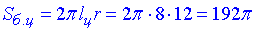
Площа поверхні утвореного тіла обертання:
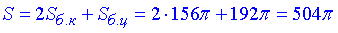
S/π=504.
Відповідь: 504.
Думаю, що наведені відповіді будуть для Вас корисними не тільки при ЗНО підготовці, а й на перших курсах ВУЗ-ів та останніх класах середньої школи.
Далі розглянемо завдання на площу осьового та інших перерізів.
