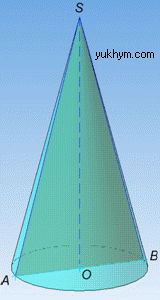
Проаналізуємо кілька готових відповідей до тестових задач із ЗНО підготовки на знаходження площі розгортки конуса.
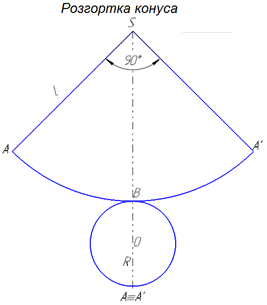
Нагадаємо, що розгорткою бічної поверхні конуса називають круговий сектор, який утворюється при розрізі бічної поверхні по твірній та розгортанні на площині.
Радіус кругового сектору за побудовою дорівнює твірній в конусі, довжина дуги сектора відповідно рівна довжині кола в основі конуса.
Таким чином площа бічної поверхні конуса фактично рівна площі її розгортки.
Площа кругового сектора (розгортки бічної поверхні конуса) знаходять за формулою
S=π•l•α/360 , де α — градусна міра дуги AA'.
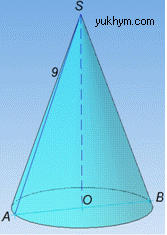
Задача 39.7 Розгорткою бічної поверхні конуса є сектор, радіус якого дорівнює 9 см, а дуга – 120 градусів.
Знайти радіус конуса.
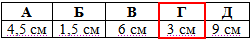
Розв'язання: Маємо розгортку конуса – сектор з радіусом l=9 см і кутом ∠ASA'=120, причому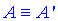 
(тобто точки A та A' на конусі співпадають).
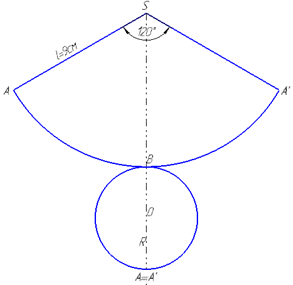
Запам'ятайте твердження, яке є справедливим для усіх задач на розгортку конуса:
Радіус сектора є твірною для конуса, довжина дуги сектора дорівнює довжині кола – основи конуса.
Знайдемо довжину дуги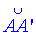 
розгортки конуса – сектора SABA':
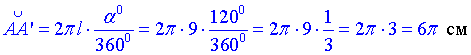
де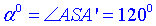 
– градусна міра дуги, або центрального кута (∠ASA'), що вписаний в цю дугу.
Отримали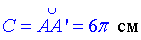 
– довжину кола основи конуса.
Але довжина кола обчислюється за формулою:
C=2πR, де R – радіус (кола) основи конуса.
Отже, 2πR=6π, звідси отримаємо R=3 см.
Відповідь: 3 см – Г.
Задача 39.16 Півкруг згорнули в конус. Знайти кут при вершині осьового перерізу цього конуса.
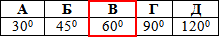
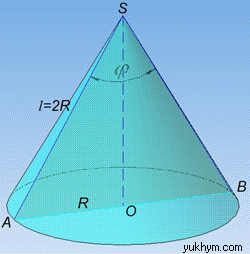
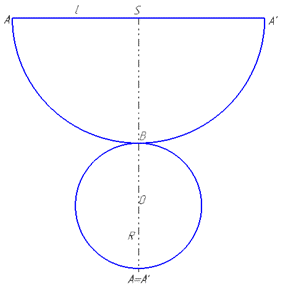
Розв'язання: Маємо розгортку конуса – сектор з радіусом l і кутом ∠ASA’=180, адже в умові сказано, що розгорткою конуса є півкруг, величина якого становить 180, на рисунку (тобто точки A та A’ на конусі співпадають).
Знайдемо довжину дуги 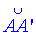розгортки конуса – сектора SABA’:
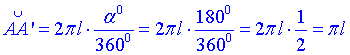
де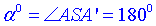 
– градусна міра дуги, або центрального кута (∠ASA’), що вписаний в цю дугу.
Отримали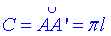 
– довжину кола основи конуса.
Але довжина кола обчислюється за формулою:
C=2πR, де R – радіус (кола) основи конуса.
Отже, 2πR=πl, звідси отримаємо l=2R.
В осьовому перерізі – ΔSAB (дивись І абзац задачі 39.1) отримали: SA=SB=AB, тому ΔSAB – рівносторонній.
У рівностороннього трикутника всі кути рівні та дорівнюють 60.
Звідси ∠ASB=60 – кут при вершині осьового перерізу заданого конуса.
Відповідь: 60 – В.
Задача 39.17 Розгорткою бічної поверхні конуса є сектор з дугою alpha.
Знайти alpha, якщо висота конуса дорівнює 4 см, а радіус основи – 3 см.
Розв'язання: Маємо конус з висотою H=SO=4 см і радіусом основи R=AO=3 см.
Розглянемо осьовий переріз заданого конуса – ΔSAB (дивись І абзац задачі 39.1).
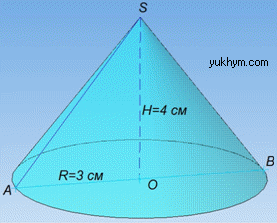
Із прямокутного ΔSAO (∠AOS=90), у якого SO=4 см і AO=3 см – катети, за теоремою Піфагора знайдемо гіпотенузу SA=l – твірну заданого конуса:
SA^2=SO^2+AO^2, звідси
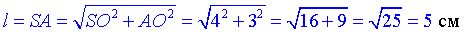
Довжину кола – основи заданого конуса знаходимо за формулою:
r=2π•R=6π см.
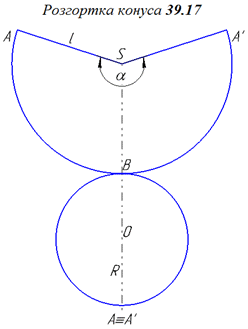
Маємо розгортку конуса – сектор з радіусом l=5 см і кутом ∠ASA'=alpha, на рисунку 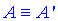( точки A та A’ співпадають).
Ще раз нагадаємо, що радіус сектора є твірною для конуса, довжина дуги сектора рівна довжині кола – основи конуса, тобто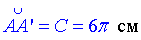 
Знайдемо величину дуги alpha сектора SABA’ розгортки заданого конуса:
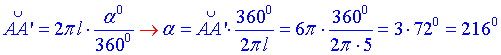
отже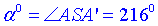 
– градусна міра дуги, або центрального кута (∠ASA’), що вписаний в цю дугу.
Відповідь: 216 – Г.
Задача 39.29 Висота конуса дорівнює 6. Розгорткою бічної поверхні цього конуса є сектор з центральним кутом 120.
Визначити об'єм V конуса. У відповідь записати V/π.
Розв'язання: Об'єм конуса обчислюють за формулою:
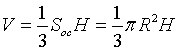, де Soc=πR2 – площа основи конуса (площа круга);
H=SO – висота конуса.
Маємо конус з висотою H=SO=6, розгорткою якого є сектор з радіусом l і центральним кутом ∠ASA'=120, причому (точки A та A' на конусі співпадають).
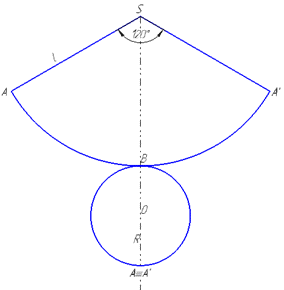
Знайдемо довжину дуги 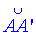розгортки конуса – сектора SABA':
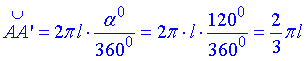
де 
– градусна міра дуги, або центрального кута (∠ASA'), що вписаний в цю дугу.
Отримали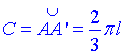 
– довжину кола основи конуса.
Але довжина кола обчислюється за формулою:
C=2πR, де R – радіус (кола) основи конуса.
Отже, 2πR=2/3πl, звідси отримаємо R=l/3, або l=3R. В осьовому перерізі ΔSAB (дивись І абзац задачі 39.1) розглянемо прямокутний трикутник AOS (∠AOS=90), в якому SA=l – гіпотенуза, а SO=6 і AO=R – катети.
За теоремою Піфагора знайдемо залежність довжини твірної SA=l від радіуса основи AO=R:
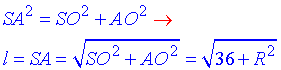
звідси, враховуючи, що l=3R, маємо
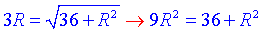
отже отримаємо
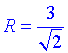
Об'єм конуса:
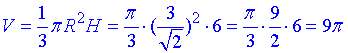
V/π=9.
Відповідь: 9.
Задача 39.36 Бічною поверхнею конус розгортається у чверть круга.
Визначити повну поверхню цього конуса, якщо площа його осьового перерізу дорівнює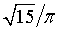 
Розв'язання: Маємо конус з площею осьового перерізу
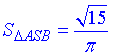
(дивись І абзац задачі 39.1), розгорткою якого є чверть круг – сектор з радіусом l і центральним кутом ∠ASA'=90, причому 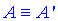(тобто точки A і A' на конусі співпадають).
Знайдемо довжину дуги AA' розгортки конуса – сектора SABA':
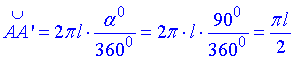
де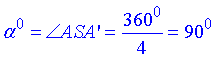 
– градусна міра дуги (чверть круга), або центрального кута (∠ASA'), що вписаний в цю дугу.
Отримали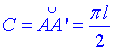 
– довжину кола основи конуса.
Але довжина кола обчислюється за формулою:
C=2πR, де R – радіус (кола) основи конуса.
Отже, 2πR=πl/2, звідси отримаємо R=l/4, або l-4R.
Площа осьового перерізу, ΔASB:
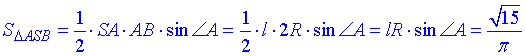
Оскільки, R=l/4, то R/l=1/4=cos(∠A) у прямокутному ΔSAO (∠SAO=90), де l=SA – гіпотенуза, R=AO – прилеглий катет до ∠A.
Звідси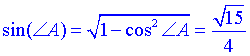 
.
Тоді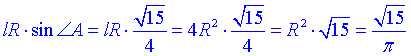 
, тобто 
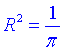і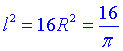 
.
Площа бічної поверхні конуса (дорівнює площі його розгортки):
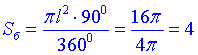
Площа основи конуса:
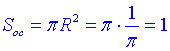
Площа повної поверхні конуса:
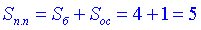
Відповідь: 5.
Тут наведені відповіді до завдань на розгортку конуса лише з одного посібника для підготовки до ЗНО.
Загалом подібних задач можна придумати чи віднайти в інтернеті ще сотні.
Всі вони між собою певною мірою перекликаються та похожі, тому наведені тут формули справедливі для обчислення безлічі задач на розгортку конуса.
Вчіть теорію та нехай у Вас не буде труднощів як на практичних з геометрії, так і в навчанні у ВУЗ-ах.
