Розглянемо кілька готових відповідей до тестових задач із ЗНО, в яких потрібно визначити площу бічної поверхні конуса.
Для розрахунків Вам потрібні базові знання з геометрії за 10-11 клас та бажання вивести нові формули.
Задача39.2 Твірна конуса дорівнює l, а кут між твірною і висотою – beta.
Визначити площу бічної поверхні конуса.
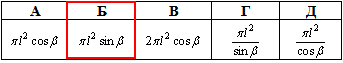
Розв'язання: Площа бічної поверхні конуса обчислюється за формулою:
Sb=πRl, де R=AO=BO – радіус основи конуса;
l=SA=SB – твірна конуса.
Маємо конус з твірною SA=l (за умовою задачі) й ∠ASO=beta – кут між твірною SA=l і висотою SO=H.
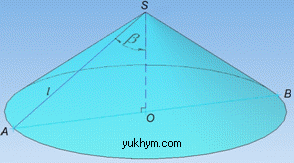
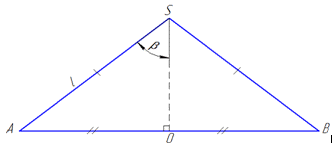
Розглянемо прямокутний ΔAOS (∠AOS=90), в якому SA=l – гіпотенуза і ∠ASO=beta – кут, що є протилежним до катета AO=R.
За означенням синуса гострого кута прямокутного трикутника знайдемо катет AO=R:
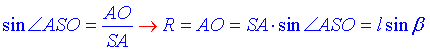
Отже, R=AO=BO=l•sin(beta) – радіус основи конуса.
Площа бічної поверхні конуса:
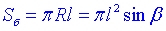
Відповідь: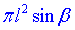 
– Б.
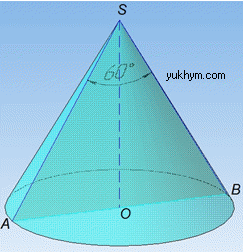
Задача 39.14 Найбільший кут між твірними конуса дорівнює 60.
Знайти відношення бічної поверхні до площі основи конуса.
Розв'язання: Площа бічної поверхні конуса обчислюється за формулою:
Sb=πRl, де R=AO=BO – радіус основи конуса;
l=SA=SB – твірна конуса.
Площа основи конуса (круга):
Soc=πR2.
Маємо конус з найбільшим кутом між твірними – ∠ASB=60, оскільки найбільший кут між твірними – це кут між сторонами SA і SB осьового перерізу конуса – трикутника SAB (про осьовий переріз дивись І абзац задачі 39.1).
Оскільки ∠ASB=60, то за теоремою про суму кутів трикутника і властивістю кутів при основі у рівнобедреного трикутника ΔSAB, маємо:
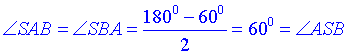
тобто ∠SAB=∠SBA=∠ASB=60. Отже, ΔSAB – рівносторонній (у нього всі кути і сторони рівні), звідси SA=SB=AB=2R, тобто l=2R.
Для заданого конуса маємо:
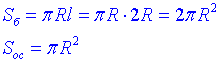
Складемо відношення бічної поверхні до площі основи конуса:
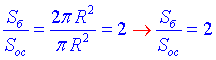
Відповідь: 2 – Б.
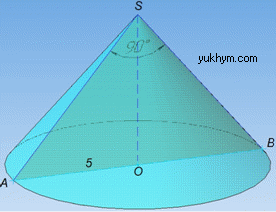
Задача 39.25 Осьовим перерізом конуса є прямокутний трикутник.
Знайти площу S бічної поверхні конуса, якщо радіус основи конуса дорівнює 5.
У відповідь записати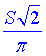 
Розв'язання: Площа бічної поверхні конуса обчислюється за формулою:
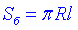, де R=A=BO=5 – радіус основи конуса;
l=SA=SB – твірна конуса.
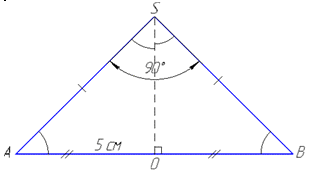
Маємо конус з радіусом R=AO=5 і з осьовим перерізом, яким є прямокутний ΔSAB (∠ASB=90).
Оскільки осьовий переріз ΔSAB – рівнобедрений з основою AB (R=AO=BO=5) і бічними сторонами SA=SB (дивись І абзац задачі 39.1), то ∠SAB=∠SBA=45 (впливає із суми кутів трикутника і рівності кутів при основі рівнобедреного трикутника), а також ∠ASO=∠BSO=45 (SO – бісектриса).
Звідси слідує, що ∠SAO=∠ASO=45, тому прямокутний ΔAOS (∠AOS=90) – рівнобедрений з основою SA і бічними сторонами AO=SO=5.
Отримали, що SO=5 – висота конуса.
Із прямокутного ΔAOS (∠AOS=90), у якого SO=5 і AO=5 – катети, за теоремою Піфагора знайдемо гіпотенузу SA=l – твірну заданого конуса:
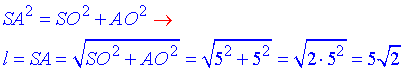
Площа бічної поверхні конуса:
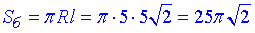
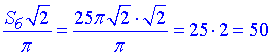
Відповідь: 50.
Задача 39.37 У правильній чотирикутній піраміді плоский кут при вершині дорівнює 60.
Визначити площу бічної поверхні конуса, описаного навколо піраміди, якщо її висота дорівнює
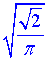
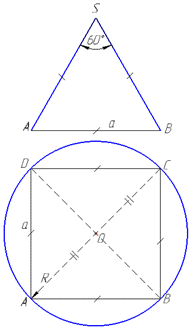
Розв'язання: Площа бічної поверхні конуса обчислюється за формулою:
Sb=πRl, де R=A=CO – радіус основи конуса;
l=SA=SB – твірна конуса.
Конус описаний навколо піраміди, якщо основа конуса описана навколо основи піраміди, а висота конуса дорівнює висоті піраміди.
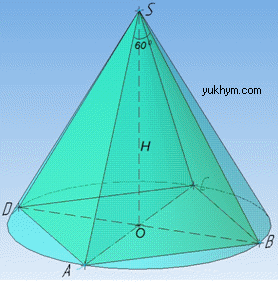
Маємо правильну чотирикутну піраміду SABCD, у якої висота піраміди:
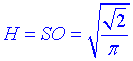і ∠ASB=60 – плоский кут при вершині.
Оскільки правильна чотирикутна піраміда вписана у конус, то осьовий переріз піраміди є осьовим перерізом конуса, тобто ΔSAC (про осьовий переріз конуса дивись І абзац задачі 39.1).
В основі піраміди лежить правильний чотирикутник (тобто квадрат) ABCD, який вписаний в основу конуса.
Тому центр цього круга, точка O, знаходиться на перетині діагоналей AC і BD квадрата ABD.
Нехай сторона квадрата дорівнює a, тоді
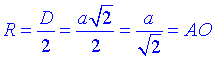
– радіус описаного навколо квадрата кола, радіус основи конуса.
У заданій піраміді SA=SB=AB=a, оскільки рівнобедрений ΔSAB (у правильної піраміди всі бічні ребра рівні) з кутом 60 – рівносторонній.
Розглянемо прямокутний ΔSAO (∠SOA=90), у якого відомі два катети –
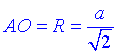, SO=H та гіпотенуза – SA=a.
За теоремою Піфагора встановлюємо, що
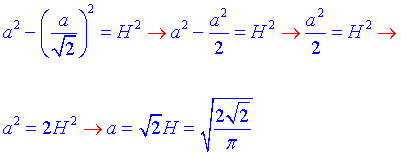
Отже,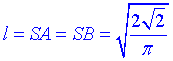 
– довжина бічного ребра піраміди, твірна конуса;
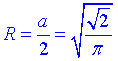– радіус описаного кола (основи конуса) навколо квадрата ABCD.
Площа бічної поверхні конуса:
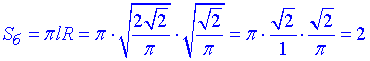
Sb=2.
Відповідь: 2.
Далі розглянемо задачі на повну поверхню конуса та площі осьового та інших перерізів.
