Розберемо готові відповіді до завдань на обчислення площі осьового та інших перерізів. Задачі підібрано із посібника для ЗНО підготовки.
Нагадаємо, що осьовим перерізом називають такий, що проходить через вісь конуса.
Осьовим перерізом конуса завжди є рівнобедрений трикутник, висота якого рівна висоті конуса, а основа трикутника рівна діаметру кола в основі конуса.
Інші перерізи утворюють площинами, які перетинають конус під певним кутом до його осі.
Окремий випадок – це площини паралельні основі конуса і розміщені на певній висоті від неї.
Такого сорту задачі нами відібрані та далі наведені їх розв'язки.
Задача 39.5 Осьовим перерізом конуса є прямокутний трикутник. Радіус основи конуса дорівнює 6.
Знайти площу осьового перерізу конуса.
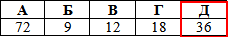
Розв'язання: Маємо конус з радіусом R=AO=6 і з осьовим перерізом, яким є прямокутний ΔSAB (∠ASB=90).
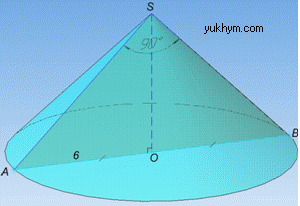
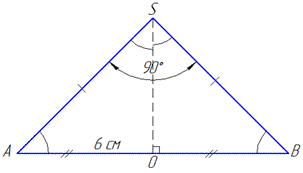
Оскільки осьовий переріз ΔSAB – рівнобедрений з основою AB (R=AO=BO=6) та бічними сторонами SA=SB (дивись І абзац задачі 39.1), то ∠SAB=∠SBA=45 (впливає із суми кутів трикутника і рівності кутів при основі рівнобедреного трикутника), а також ∠ASO=∠BSO=45 (SO – бісектриса).
Звідси слідує, що ∠SAO=∠ASO=45, тому прямокутний ΔAOS (∠AOS=90) – рівнобедрений з основою SA і бічними сторонами AO=SO=6.
Отримали, що SO=6 – висота ΔSAB, проведена до сторони AB=12
(AB=AO+BO=12, оскільки SO – одночасно медіана і висота рівнобедреного ΔSAB).
Площа ΔSAB – осьового перерізу конуса:
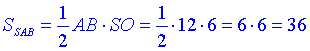
Відповідь: 36 – Д.
Задача 39.6 Радіус основи конуса дорівнює 8 см, а його твірна – 10 см. Знайти площу осьового перерізу конуса.
Розв'язання: Маємо конус з радіусом R=AO=8 см і твірною l=SA=10 см.
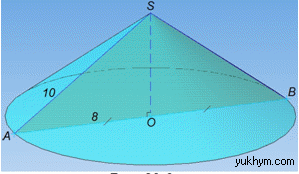
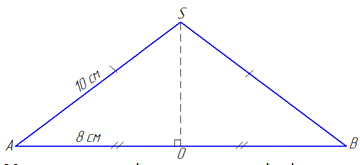
Осьовим перерізом конуса є рівнобедрений ΔSAB (далі дивись І абзац задачі 39.1). Отже, AB=2R=2•8=16 см.
Розглянемо прямокутний трикутник AOS (∠AOS=90), в якому SA=1 см – гіпотенуза та AO=8 см – катет.
За теоремою Піфагора знайдемо катет SO=H – висоту конуса:
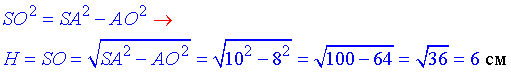
Отже, H=SO=6 см – висота конуса та одночасно ΔSAB.
Площа ΔSAB – осьового перерізу конуса:
.
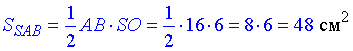Відповідь: 48 см2 – А.
Задача 39.24 Установити відповідність між кутом нахилу твірної конуса (1–4) та відношенням площ його основи та осьового перерізу (А – Д).
Ця задача є оберненою до задачі 39.15
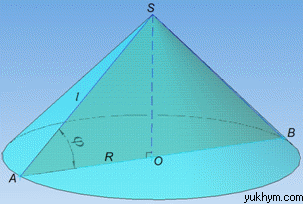
Розв'язання: Площа основи конуса обчислюється за формулою:
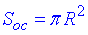
де R=AO=BO – радіус основи конуса;
l=SA=SB – твірна конуса.
Площа осьового перерізу – ΔSAB:
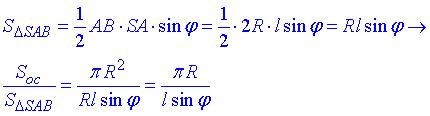
(про осьовий переріз дивись І абзац задачі 39.1), де phi – кут між твірною і діаметром конуса – кут нахилу твірної до площини основи конуса.
За означенням косинуса гострого кута прямокутного ΔAOS (∠AOS=90), у якого SA=l – гіпотенуза та AO=R – прилеглий катет до кута ∠SAO=phi маємо:
cos(phi)=R/l, звідси отримаємо
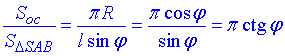
Обчислимо відношення площ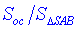 
в залежності від кута phi в кожному випадку:
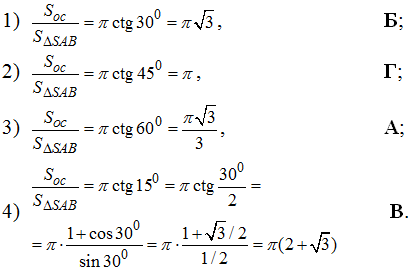
Задача 39.8 Висоту конуса поділено на чотири рівні відрізки і через точки поділу паралельно основі проведено площини.
Визначити площу найбільшого перерізу, якщо площа основи дорівнює S.
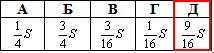
Розв'язання: Площина, яка перетинає конус та проходить паралельно основі відтинає подібний конус.
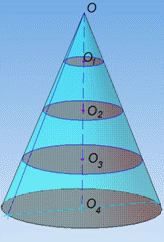
А у подібних конусів відповідні площі відносяться як квадрати їх відповідних лінійних розмірів. Найбільшу площу має переріз, який знаходиться найближче до основи заданого конуса (тобто переріз 3), оскільки конус з основою, яким є переріз 3 має найбільшу висоту.
Оскыльки площини проходять через точки, які ділять висоту заданого конуса на 4 рівні частини, то висота подібного конуса з перерізом 3 має висоту
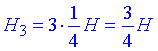
(оскільки вона складається з 3 частин чверті всієї висоти), де H – висота заданого конуса.
За умовою задачі S – площа основи заданого конуса, тоді S3 – площа перерізу 3.
Складемо відношення і знайдемо S3:
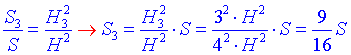
Отже, S3=9•S/16 – площа найбільшого перерізу.
(Ця задача є аналогічною до задачі 37.10 (треба було слово «піраміда» змінити на «конус»), оскільки конус і піраміда відрізняються основами: у піраміди в основі лежить многокутник, а у конуса – круг).
Відповідь: 9/16•S – Д.
Задача 39.10 Радіус основи конуса дорівнює r.
Визначити площу перерізу, який проходить через вершину конуса і хорду основи, яка стягує дугу 60, якщо площина перерізу утворює з площиною основи конуса кут 30.
Розв'язання: Розглянемо рівнобедрений ΔAOB, у якого AO=OB=r – бічні сторони, як радіуси основи конуса, а AB – основа, тобто хорда (за умовою задачі).
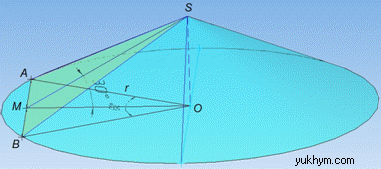
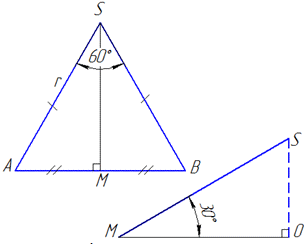
Проведемо висоту OM до основи AB у рівнобедреному ΔAOB (AB⊥OM), тоді OM – медіана і бісектриса ΔAOB (за властивістю), тобто AM=BM=AB/2 і
∠AOM=∠AOB/2=60/2=30
оскільки ∠AOB=60 є центральним кутом вписаним у круг (основу конуса), що опирається на відповідну дугу. За теоремою про суму кутів ΔAB і властивістю про рівність кутів при основі рівнобедреного ΔAOB маємо:
∠OAB=∠OBA=∠AOB=60.
Звідси слідує, що ΔAOB – рівносторонній (у нього всі сторони і всі кути рівні), тому AB=AO=OB=r і AM=BM=r/2.
Розглянемо прямокутний ΔAM (∠AMO=90), у якого AO=r – гіпотенуза.
За означенням косинуса гострого кута прямокутного трикутника знайдемо прилеглий катет OM до кута ∠AOM=30.
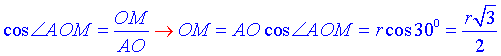
Розглянемо прямокутний ΔSOM (∠SOM=90), у якого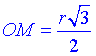 
– прилеглий катет до кута ∠SMO=30 – кута між перерізом, тобто ΔASB і площиною основи конуса.
За означенням косинуса гострого кута прямокутного трикутника знайдемо гіпотенузу SM – висоту ΔASB, оскільки SM⊥AB (за теоремою «про три перпендикуляри»):
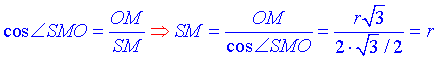
Площа перерізу – ΔASB:
.
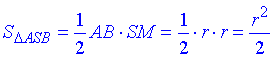Відповідь: r2/2 – Д.
Задача 39.13 Осьовим перерізом конуса є правильний трикутник зі стороною 2r.
Визначити площу перерізу, проведеного через дві твірні, кут між якими дорівнює 30.
Розв'язання: Маємо конус з осьовим перерізом ΔSAB (про осьовий переріз дивись І абзац задачі 39.1).
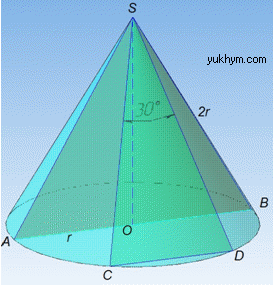
Отже, SA=SB=AB=2r (за умовою задачі). Твірна конуса – відрізок, проведений з вершини конуса в точку, що належить границі основи конуса. Проведемо твірні SC і SD заданого конуса, кут між якими дорівнює 30, тобто ∠CSD=30.
Оскільки всі твірні конуса рівні, то SC=SD=2r.
Отже, отримали переріз конуса – трикутник SCD зі сторонами SC=SD=2r і кутом ∠CSD=30 між ними.
Площа ΔSCD:
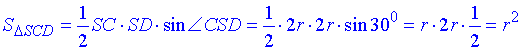
Відповідь: r2 – А.
На ЗНО тестах чи практичних з геометрії Вас можуть чекати подібні до наведених завдання, тому зберігайте посилання на сайт в улюблені закладки та використовуйте в навчанні.
