Радіус кола. Довжина хорди. Діаметр круга

Продовжуємо розбирати відповіді до тестових завдань для ЗНО підготовки і сьогодні переглянемо лише ті завдання з 35 розв'язаних, де потрібно знайти лінійні розміри в колі чи крузі. Обчислення довжини дуги винесено в окрему статтю. Формули, що тут даються є загальними для математики, тому ними обов'язково Ви повинні вміти користуватися.

Задача 34.2 Знайти радіус кола, якщо довжина кола дорівнює 24π см.

Розв'язання: Почнемо з формули для знаходження довжини кола:
C=2πR, де C=24π см, звідси виражаємо радіус

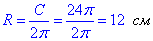
Запам'ятайте виведення цієї формули, адже є багато подібних завдань.
Відповідь: 12 см – Б.

Задача 34.4 Знайти радіус кола, в якого кутова величина дуги завдовжки π см дорівнює 45⁰.

Розв'язання: Повторимо формулу для обчислення довжини дуги кола:

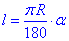
де 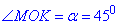- величина центрального кута;
l=π см - довжина дуги кола.
OM=OK=R - радіус кола, звідси отримуємо

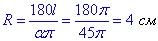
Відповідь: 4 см – Д.

Задача 34.7 Знайти діаметр круга, площа якого дорівнює π см².

Розв'язання: Формула для обчислення площі круга:
S= πR², де R - радіус круга.

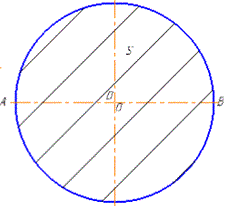
Звідси виводимо формулу радіуса круга через його площу

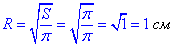
Виведення формули радіуса круга теж вартує запам'ятати.
За означенням:
D=2R=2 см - діаметр круга.

Відповідь: 2 см – А.

Задача 34.19 Три кола, радіуси яких дорівнюють 2, 3 і 10, попарно дотикаються зовні.
Знайти радіус кола, яке вписане в трикутник, утворений центрами цих кіл.

Розв'язання: Оскільки три кола попарно дотикаються зовні в точках A, B і C, то відрізки O₁O₃, O₁O₂ і O₂O₃ проходять через ці точки відповідно

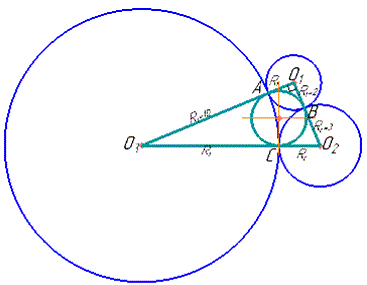
(це випливає із властивості, що дотична в точці дотику перпендикулярна до радіуса кола), де O₁, O₂ і O₃ - центри кіл, що дотикаються зовні.
Звідси отримуємо довжини сторін трикутника:

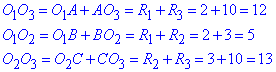
Знайдемо півпериметр трикутника O₁O₂O₃:

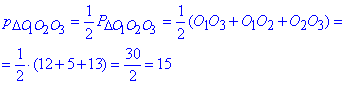
Помічаємо, що ΔO₁O₂O₃ є прямокутний (13²=12²+5²) з катетами O₁O₃=12, O₁O₂=5 і гіпотенузою O₂O₃=13, тому його площа рівна півдобутку катетів:

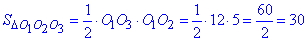
Знайдемо радіус кола вписаного в ΔO₁O₂O₃ за формулою частки площі трикутника до його півпериметру:

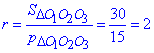
Відповідь: 2 – Г.

Задача 34.20 l(x) - довжина хорди, проведеної на відстані x від центра кола.
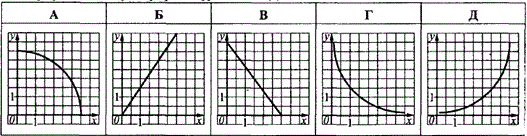
Який із наведених графіків може бути графіком функції l=l(x)?

Розв'язання: Побудуємо схематичний рисунок

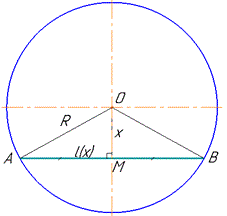
За умовою маємо коло з центром у точці O і радіусом R=OA=OB.
В колі проведена хорда AB=l на відстані OM=x від центра кола.
Отримали рівнобедрений ΔOAB з основою AB=l, бічними сторонами R=OA=OB та висотою OM=x, що проведена до основи AB.
За властивістю рівнобедреного ΔOAB маємо:
AM=MB=l/2 і AM⊥OM (∠AMO=90).
За теоремою Піфагора у прямокутному ΔOAM отримаємо:

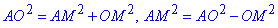
звідси
Отже, 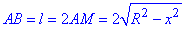, тобто 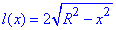(частина еліпса з центром в початку координат (0;0)).
Графік отриманої залежності зображений на рисунку А.
Відповідь: А.

Задача 34.21 З точки кола проведено дві перпендикулярні хорди a та b.
Установити відповідність між довжинами цих хорд (1–4) та довжиною кола (А–Д).

Розв'язання: Маємо коло з центром у точці O, дві хорди AC=b см і BC=a см (∠ACB=90 за умовою).

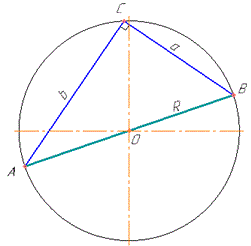
Оскільки ∠ACB - прямий, то він спирається на діаметр AB.
Із прямокутного трикутника ΔACB за теоремою Піфагора знайдемо гіпотенузу AB:
AB²=AC²+BC², звідси

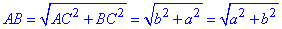
Вона одночасно є 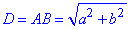- діаметром кола.
Виводимо формулу для довжини кола за хордами

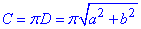
Обчислимо довжину кола для заданих довжин хорд a та b:
1. a=12 см і b=16 см , 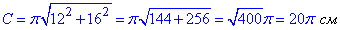, 1 – Б
2. a=5 см і b=12 см , 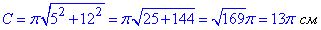см, 2 – Г
3. a=3 см і b=4 см , 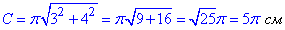см, 3 – А
4. a=6 см і b=8 см , 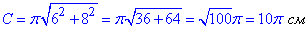см, 2 – В

Задача 34.22 Установити відповідність між довжинами сторін квадрата (1–4) та радіусами вписаних у квадрати кіл (А–Д).

Розв'язання: Маємо квадрат зі стороною a см та вписане коло з радіусом r см.

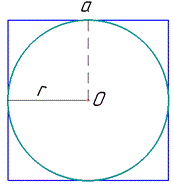
За властивістю квадрата і кола вписаного в нього випливає, що радіус вписаного в квадрат кола r дорівнює половині сторони квадрата a, тобто r=a:2.
1. a=2 см, тоді r=2:2=1, 1 – В
2. a=6 см, тоді r=6:2=3, 2 – А
3. a=10 см, тоді r=10:2=5, 3 – Д
4. a=30 см, тоді r=30:2=15, 4 – Б.

Задача 34.32 У прямокутну трапецію з основами 1 і 3 вписано коло. Знайти радіус вписаного кола.
Розв'язання: Нехай маємо прямокутну трапецію ABCD, AD||BC,BC=1, AD=3, AB⊥AD, AB⊥BC і вписане в трапецію коло з центром у точці O.

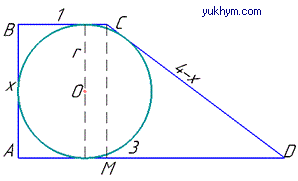
Позначимо AB=x, тоді, за властивістю вписаного кола у чотирикутник, суми протилежних сторін чотирикутника рівні, тобто AB+CD=AD+BC, x+CD=3+1, звідси CD=4-x.
Оскільки коло вписане у трапецію, то радіус перпендикулярний до сторін трапеції (в точках дотику), тому діаметр вписаного кола дорівнює висоті трапеції.
Проведемо висоту CM трапеції ABCD. Оскільки трапеція ABCD прямокутна, то CM=AB=x, звідси AM=BC=1, MD=AD-AM=3-1=2.
У прямокутному ΔCMD (∠CMD=90) за теоремою Піфагора запишемо
CD²=CM²+MD², звідси (4-x)²=x²+2²,
16-8x+x²=x²+4, 16-8x=4, 8x=12, звідси x=1,5.
Отже отримали: d=CM=AB=1,5 - висота трапеції ABCD і діаметр вписаного кола.
Знайдемо радіус r вписаного кола в прямокутну трапецію ABCD:
R=d:2=1,5:2=0,70.
Відповідь: 0,70.

Задача 34.16 У прямокутник ABCD вписано три круги одного й того самого радіуса.

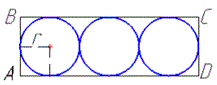
Визначити довжину сторони BC, якщо загальна площа кругів дорівнює 3π.

Розв'язання: За умовою задачі маємо 3 однакових круги із загальною площею 3π, тоді площа одного круга:
S₁=π з радіусом r=1, де S= πR² - площа круга.
d=2r=2 - діаметр одного круга, тому BC=3d=3•2=6.
Відповідь: 6 – В.

Задача 34.31 На рисунку сторона квадрата дорівнює 5. Кожна його вершина є центром кола радіуса 5. Знайти периметр P замальованого криволінійного чотирикутника обмеженого цими колами. У відповідь записати 3P/π.
Розв'язання: Нехай маємо квадрат ABCD зі стороною a=5.

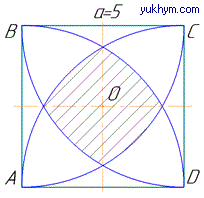
Проведемо частини чотирьох кіл з центрами в кожній вершині квадрата і довжиною C, які лежать в середині квадрата ABCD. Центр квадрата O є центром симетрії, тому всі точки цієї фігури є симетричними відносно цього центра, звідки слідує, що вершини заштрихованого криволінійного чотирикутника розділяють чверть кола на три рівних частини, тобто довжина однієї частини:
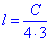(чверть кола ще на три поділили).
Це твердження потребує строгого доведення, яке тут не подається.
Знайдемо периметр P замальованого криволінійного чотирикутника:

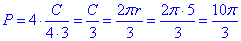
звідси

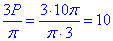
Відповідь: 10.

Можливо не усі завдання напряму стосуються радіусу кола та довжини хорд, але такі завдання мають місце при поступленні у ВУЗи і їх Ви повинні вміти розв'язувати. Далі підуть приклади на центральний та внутрішні кути в колі та площу круга, або певних фігур на основі кругів.

Вас може зацікавити:
1. Площа круга. Площа кругового сектора
2. Довжина кола. Задачі на довжину дуги кола
3. Кути в колі. Кути дуг
4. Рівнобедрені трикутники. 25 задач на площу, периметр, радіус