Чотирикутна призма. Задачі з відповідями

В інтернеті Ви можете зустріти безліч умов до задач на чотирикутну призму, однак не всі вони містять готові відповіді. Далі наведені готові розв'язки до посібника із ЗНО підготовки, які навчать вас знаходити площу повної поверхні призми, площу основи, об'єм, кути і т.д. Проаналізувавши відповіді, Ви можете пригадати потрібні формули та властивості призм. Приклади в першу чергу необхідні школярам 10-11 класів для покращення знань з геометрії, далі абітурієнтам для підготовки до вступу у ВУЗи, а також батькам для перевірки правильності обчислень їх дітей та вчителям для підготовки уроків. Нові малюнки до завдань допоможуть Вам швидко розібратися з обчисленнями.


Пропонуємо завантажити відповіді (Посібник для підготовки до зовнішнього незалежного тестування з математики).
Автори: Анатолій Капіносов, Галина Білоусова, Галина Гап'юк, Сергій Мартинюк, Лариса Олійник, Петро Ульшин, Олег Чиж

 

Тема 36.4 Чотирикутна призма

Задача 36.9 Знайти площу повної поверхні правильної чотирикутної призми, сторона основи якої дорівнює a, а висота – H.


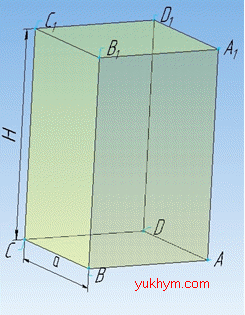
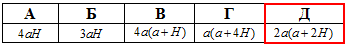
Розв'язання: Площа повної поверхні правильної призми:
Sn=2Soc+Sb.
В основі правильної чотирикутної призми лежить квадрат зі стороною a.
Тому площа основи:
Soc=a²,
периметр основи:
Poc=4a.
Площа бічної поверхні:
Sb=Soc•H=4aH.
Площа повної поверхні правильної чотирикутної призми:
Sn=2Soc+Sb=2a²+4aH=2a(a+2H).
Відповідь: 2a(a+2H) – Д.

Задача 36.10 В основі прямої призми лежить рівнобічна трапеція з основами 4 см і 10 см і бічною стороною 5 см. Бічне ребро призми дорівнює 10 см.
Обчислити повну поверхню призми.


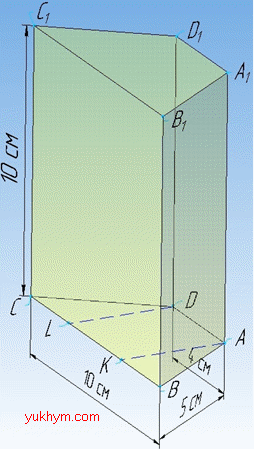
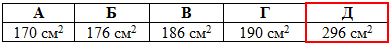
Розв'язання: Площа повної поверхні прямої призми:
S_п=2Soc+Sb.
В основі прямої призми лежить рівнобічна трапеція з основами AD=4 см і BC=10 см і бічною стороною AB=CD=5 см.

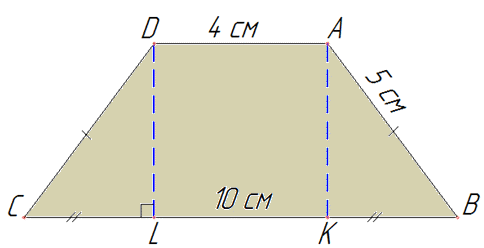
Знайдемо висоту DL трапеції.

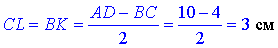
Із прямокутного трикутника DLC (∠DLC=90, бо DL⊥BC, CD=5 см – гіпотенуза і CL=3 см – катет) знайдемо катет DL.
DL²=CD²-CL², звідси

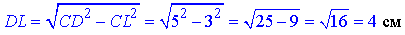
Площа основи – трапеції ABCD:

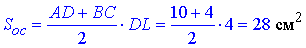
Периметр основи:
Poc=AB+BC+CD=2•5+10+4=24 см.
Площа бічної поверхні:
S_б=Poc•h=24•10=240 см².
Площа повної поверхні прямої призми:
S_п=2Soc+Sb=2•28+240=296 см².
Відповідь: 296 см² – Д.

Задача 36.16 Діагональ правильної чотирикутної призми дорівнює 13 см, а діагональ бічної грані дорівнює 12 см. Знайти площу основи призми.


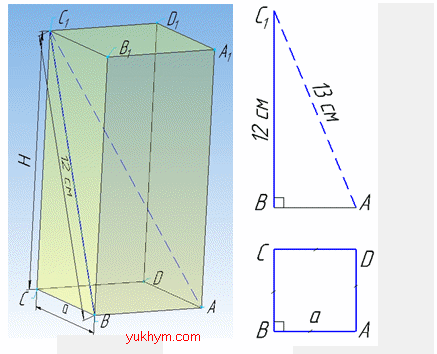
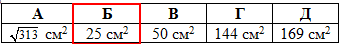
Розв'язання: В основі правильної чотирикутної призми лежить квадрат зі стороною a, тому площу основи обчислимо за формулою:
Soc=a².
У правильної призми бічне ребро перпендикулярне до площини основи CC₁⊥ (ABC), тому CC₁⊥BC. Звідси CC – перпендикуляр опущений з вершини C₁ на площину основи (на квадрат ABCD), BC₁ – похила, яка опущена з цієї ж вершини C1 на площину основи, BC – проекція похилої BC1.
Оскільки основа – квадрат ABCD, то AB⊥BC.
За теоремою «Про три перпендикуляри» маємо AB⊥BC₁, тому ΔABC₁ – прямокутний (∠ABC₁=90). З прямокутного трикутника ABC₁ (∠ABC₁=90), в якому BC<₁=12 см – катет (діагональ бічної грані) і AC₁=13 см – гіпотенуза (діагональ призми), за теоремою Піфагора знайдемо катет AB=a – довжину сторони квадрата:

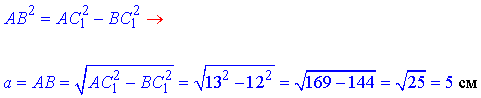
Площа основи правильної чотирикутної призми – квадрата ABCD:
Soc=a²=5²=25 см2.
Відповідь: 25 см² – Б.

Задача 36.17 У правильній чотирикутній призмі площа діагонального перерізу дорівнює S. Визначити площу бічної поверхні.


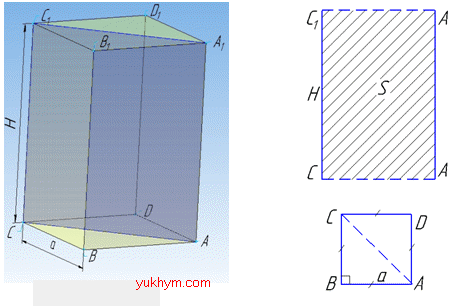
Розв'язання: Площа бічної поверхні правильної чотирикутної призми зі стороною основи a і висотою H обчислюють за формулою:
S_б=Poc•H=4aH.
У правильній чотирикутній призмі діагональним перерізом є прямокутник ACC₁A₁ зі сторонами діагоналі основи призми AC і висоти CC₁=H.
Діагональ основи правильної чотирикутної призми (квадрата ABCD):

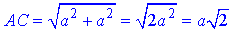
(Обчислюємо як довжину гіпотенузи AС прямокутного ΔABC (∠ABC=90)).
Площа діагонального перерізу:

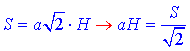
Площа бічної поверхні правильної чотирикутної призми:

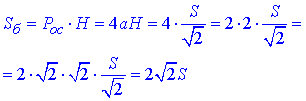
Відповідь: 2√2S – В.

Задача 36.18 Діагональним перерізом правильної чотирикутної призми є квадрат, площа якого дорівнює S. Визначити об'єм призми.


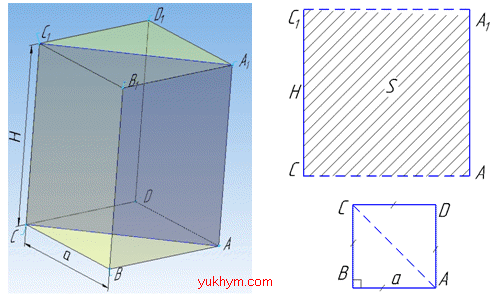
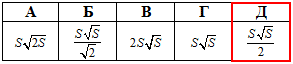
Розв'язання: Об'єм правильної чотирикутної призми зі стороною основи a і висотою H обчислюють за формулою:

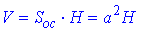
За умовою задачі у правильній чотирикутній призмі діагональним перерізом є квадрат ACC₁A₁ зі стороною діагоналі основи призми AC.
Діагональ основи правильної чотирикутної призми (квадрата ABCD):

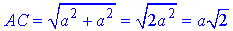
(Обчислюємо як довжину гіпотенузи AC прямокутного ΔABC).
Площа діагонального перерізу:

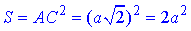
звідси отримаємо

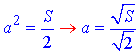
Оскільки ACC₁A₁ – квадрат, то

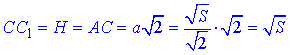
Об'єм правильної чотирикутної призми:

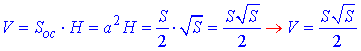
Відповідь: S√S/2 – Д.

Задача 36.20 Бічна поверхня правильної чотирикутної призми дорівнює Q, а її об'єм – V. Визначити сторону основи призми.


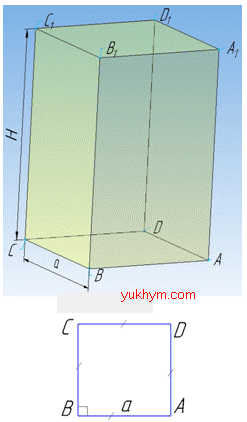
Розв'язання: В основі правильної чотирикутної призми лежить квадрат зі стороною a.
Об'єм правильної чотирикутної призми зі стороною основи a і висотою H обчислюють за формулою:
V=Soc•H=a²•H.
Бічна поверхня (площа бічної поверхні) правильної чотирикутної призми зі стороною основи a і висотою H обчислюють за формулою:
Sб=Pос•H=4aH.
За умовою задачі

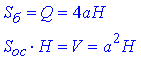
Складемо відношення

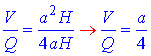
звідси отримаємо
a=4V/Q.
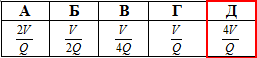
Відповідь: 4V/Q – Д.

Задача 36.21 Розгорткою бічної поверхні правильної чотирикутної призми є квадрат зі стороною 8 дм. Знайти об'єм призми.


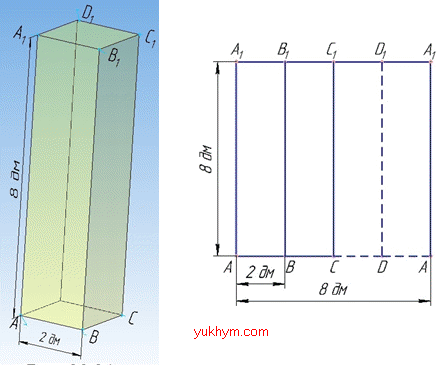
Розв'язання: Об'єм правильної чотирикутної призми зі стороною основи a і висотою H обчислюють за формулою:
V=Soc•H=a²•H.
В основі правильної чотирикутної призми лежить квадрат ABCD зі стороною a.
Оскільки розгорткою призми є квадрат зі стороною 8 дм, то висота призми дорівнює периметру основи призми:
H=Poc=8 дм.
Периметр квадрата:
Poc=4a=8 дм, звідси a=2 дм – довжина сторони основи.
Об'єм правильної чотирикутної призми:
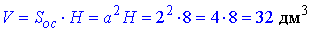 Відповідь: 32 дм³ – В.

Задача 36.24 Установити відповідність між площами діагональних перерізів (1–4), які є квадратами у правильних чотирикутних призм, та об'ємами цих призм (А–Д).


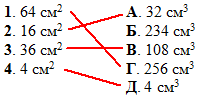
Розв'язання: (Розв'язок цієї задачі дивись у номері 36.18.)
Обчислимо об'єм призми для кожного випадку:
1) S=64 м², тоді 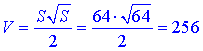Г;
2) S=16 см², тоді 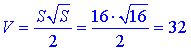А;
3) S=36 см², тоді 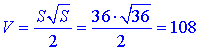В;
4) S=4 см², тоді 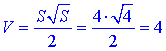Д.

Задача 36.26 Діагональ правильної чотирикутної призми утворює з площиною основи кут 45⁰. Знайти у градусах кут, утворений цією діагоналлю з площиною бічної грані.

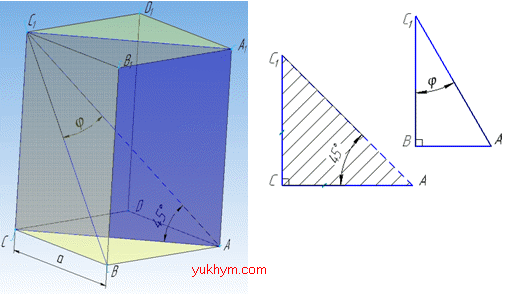
Розв'язання: У правильної призми бічне ребро (висота) перпендикулярна до площини основи (квадрата ABCD), тому бічне ребро перпендикулярне до кожного відрізка, що лежить в площині основи, тобто CC₁⊥AC, CC₁⊥BC.
Так як CC₁⊥AC, то відрізок AC (діагональ квадрата) є ортогональною проекцією діагоналі призми AC1, тому ∠C₁AC=45 – кут між діагоналлю призми і площиною основи і ΔC₁AC – прямокутний (∠ACC₁=90).
Нехай сторона основи правильної чотирикутної призми дорівнює a.
Оскільки в основі призми лежить квадрат, то за теоремою Піфагора у прямокутному ΔABC (∠ABC=90) маємо

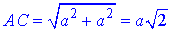
Розглянемо прямокутний трикутник C1AC, у якого ∠ACC₁=90 і ∠C₁AC=45. За теоремою про суму кутів трикутника, маємо ∠CC₁A=180-(90+45)=45.
Звідси слідує, що ΔC1AC – рівнобедрений з основою AC₁ і бічними сторонами AC=CC₁=a√2.
За теоремою Піфагора обчислимо довжину діагоналі призми AC₁: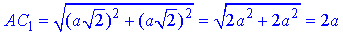
Відрізок CC₁ – перпендикуляр опущений з вершини C₁ на площину основи (на квадрат ABCD), BC₁ – похила, яка опущена з цієї ж вершини C₁ на площину основи, BC – проекція похилої BC₁.
Оскільки основа – квадрат ABCD, то AB⊥BC.
За теоремою «Про три перпендикуляри» маємо AB⊥BC₁, тому ΔABC₁ – прямокутний (∠ABC₁=90), а 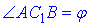– кут між діагоналлю призми AC₁ з площиною бічної грані BB₁C₁C, оскільки відрізок BC₁ – ортогональна проекція відрізка AC₁ на площину бічної грані BB₁C₁C.
Розглянемо прямокутний трикутник ABC₁, у якого ∠ABC₁=90, AC₁=2a – гіпотенуза, і AB=a – протилежний катет до кута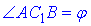
За означенням синуса гострого кута у прямокутного трикутника маємо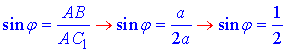
звідси слідує, що

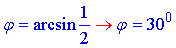
Відповідь: 30⁰.

Задача 36.34 Висота правильної чотирикутної призми дорівнює 5, а кут між діагоналями, проведеними з однієї вершини основи у двох суміжних бічних гранях, – 60⁰. Визначити площу бічної поверхні призми.

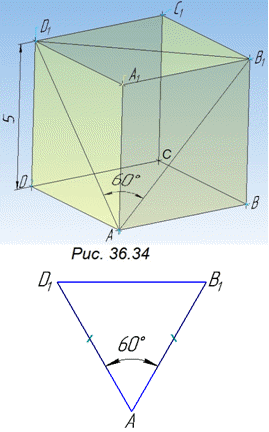
Розв'язання: Площу бічної поверхні правильної чотирикутної призми зі стороною основи a і висотою H обчислюють за формулою:
S_b=Poc•H=4a•5=20a, де H=AA₁=BB₁=CC₁=DD₁=5 – висота правильної чотирикутної призми;
a=AB=BC=CD=AD – сторона основи правильної чотирикутної призми.
Нехай ∠BAD₁ – кут між діагоналями AB₁ і AD₁ двох суміжних бічних граней AA₁B₁B і AA₁D₁D відповідно.
Проведемо відрізок B₁D₁ (діагональ грані A₁B₁C₁D₁) і розглянемо трикутник B₁A₁D₁.
Оскільки в умові задана правильна чотирикутна призма, то в основі лежать квадрати, а бічні грані є рівними прямокутниками.
У рівних прямокутників всі діагоналі рівні, тому AB₁=AD₁.
Отже, ΔB₁AD₁ – рівнобедрений з основою B₁D₁ і (за властивістю)

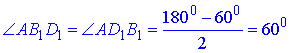
Трикутник, у якого всі кути рівні (∠AB₁D₁=∠AD₁B₁=∠B₁AD₁=60) – рівносторонній:
AB₁=AD₁=B₁D₁.
Правильна чотирикутна призма, у якої всі діагоналі граней рівні (а відповідно, і всі ребра рівні) називається кубом.
Тому довжина ребра куба:
a=H=5.
Площа бічної поверхні правильної чотирикутної призми (куба):
Sb=Poc•H=20•5=100
Відповідь: 100.

На наступному уроці розберемо складніші приклади на похилі трикутні та чотирикутні піраміди, а далі перейдемо до пірамід.  Всім школярам, для яких ця тема здається важкою рекомендуємо переглянути попередні простіші статті на паралелепіпеди та куби.

Вас може зацікавити:
1. Правильна трикутна піраміда
2. Задачі на зрізану піраміду
3. Чотирикутна призма. Задачі з відповідями
4. Задачі на похилу призму з відповідями