Розглянемо готові відповіді до задач на трикутну призму, які взято із посібника для ЗНО підготовки. Пояснення до прикладів стислі, обґрунтовані та відповідають шкільним вимогам до практичних занять з геометрії для 10-11 класів. Завдання підібрані так, що охоплюють важливі формули на площу та об'єм призми, а також допоможуть згадати необхідні для розрахунків властивості таких геометричних фігур, як трикутні призми.
Пропонуємо завантажити відповіді (Посібник для підготовки до зовнішнього незалежного тестування з математики).
Автори: Анатолій Капіносов, Галина Білоусова, Галина Гап'юк, Сергій Мартинюк, Лариса Олійник, Петро Ульшин, Олег Чиж
Тема 36.2 Трикутна призма
Задача 36.6 Основою прямої призми є прямокутний трикутник з гіпотенузою 10 см і катетом 6 см. Знайти площу бічної поверхні призми, якщо її бічне ребро дорівнює 5 см.
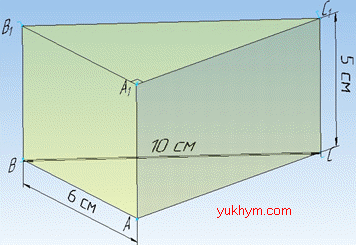
Розв'язання: Площу бічної поверхні прямої призми обчислюємо за формулою:
Sб=Poc•H,
де Poc – периметр основи;
H – висота прямої призми, довжина бічного ребра.
У прямокутному трикутнику ABC (∠BAC=90), в якому AB=6 см – катет і BC=10 см – гіпотенуза, за теоремою Піфагора знайдемо катет BC – третю сторону основи прямої призми:
AC2=BC2-AB2, звідси
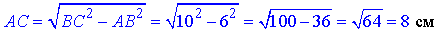
Обчислимо периметр основи прямої призми:
Poc=AB+BC+AC=6+8+10=24 см.
Обчислимо площу бічної поверхні прямої призми з бічним ребром H=CC1=5 см:
Sб=Poc•H =24•5=120 см2.
Відповідь: 120 см2 – А.
Задача 36.7 Сторона основи правильної трикутної призми дорівнює 4 см, а бічне ребро дорівнює 2√3 см. Знайти об’єм призми.
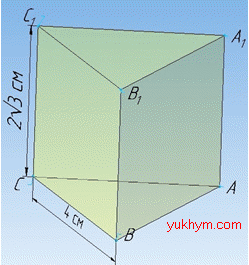
Розв'язання: Об’єм правильної призми обчислюємо за формулою:
V=Soc•H,
де Soc – площа основи;
H – висота правильної призми, довжина бічного ребра.
У правильному трикутнику ABC (AB=BC=AC=A=4 см) площа обчислюється за формулою:

Обчислимо об’єм правильної призми з бічним ребром H=CC1=2√3 см:
V=Soc•H=4√3• 2√3 =4•2•3=24 см3.
Відповідь: 24 см3 – Г.
Задача 36.8 Сторона основи правильної трикутної призми дорівнює 12 см, а діагональ бічної грані дорівнює 13 см. Знайти бічну поверхню призми.
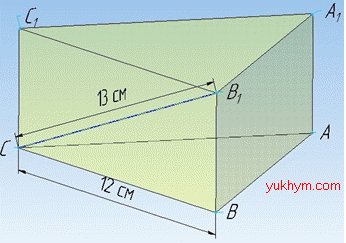
Розв'язання: Бічну поверхню правильної призми обчислюємо за формулою:
Sб=Soc•H,
де Soc – площа основи;
H – висота правильної призми, довжина бічного ребра.
У правильному трикутнику ABC (AB=BC=AC=a=12 см) периметр обчислимо за формулою
Poc=3a=3•12=36 см.
Оскільки кожна бічна грань правильної призми є прямокутник, то бічне ребро перпендикулярне до площини основи, тоді BB1⊥BC, а B1C=13 см – діагональ грані BB1C1C.
У прямокутному трикутнику B1BC (∠B1BC=90), в якому BC=12 см – катет і B1C=13 см – гіпотенуза.
За теоремою Піфагора знайдемо катет BB1=H – висоту, довжину бічного ребра правильної призми:
BB12=B1C2-BC2, звідси
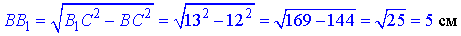
Обчислимо площу бічної поверхні правильної трикутної призми:
Sб=Soc•H=36•5=180 см2.
Відповідь: 180 см2 – Г.
Задача 36.23 Установити відповідність між сторонами основи та діагоналями (1–4) бічних граней правильних трикутних призм та площами їх бічних поверхонь (А – Д).
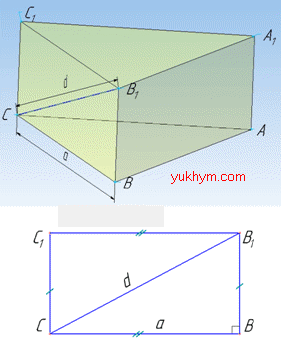

Розв'язання: Площа бічної поверхні правильної трикутної призми зі стороною основи a і висотою H обчислюють за формулою:
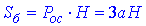
У правильній призмі бічними гранями є рівні прямокутники зі сторонами основи a і висотою H.
Бічні ребра правильної призми перпендикулярні до площини основи, а значить, і до кожного відрізка, що належить основі.
Нехай довжина діагоналі бічної грані дорівнює d.
Розглянемо прямокутний трикутник B1BC (∠B1BC=90), у якого BC=a – катет (сторона основи призми), B1C=d – гіпотенуза (діагональ бічної грані).
За теоремою Піфагора знайдемо катет, висоту призми BB1=H:
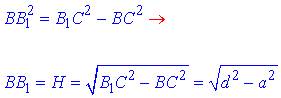
Площа бічної поверхні правильної трикутної призми:
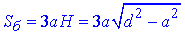
Обчислимо площу бічної поверхні призми для кожного випадку:
1) a=3 см, d=5 см, тоді
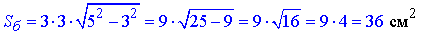 В;
В;
2) a=6 см, d=10 см, тоді
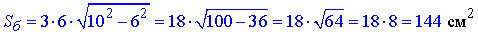 Г;
Г;
3) a=5 см, d=13см, тоді
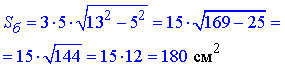 А;
А;
4) a=7 см, d=25 см, тоді
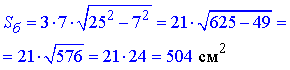 Б.
Б.
Задача 36.25 Сторона основи правильної трикутної призми дорівнює 12, а висота призми – 6. Знайти площу перерізу цієї призми площиною, яка проходить через сторону нижньої основи і протилежну вершину.
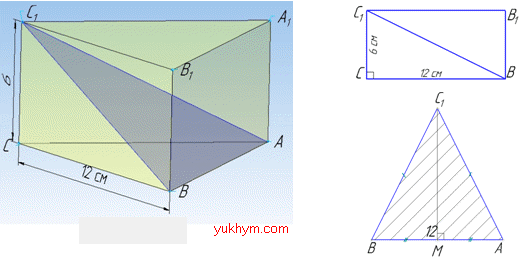
Розв'язання: Маємо правильну трикутну призму, в основі якої лежить рівносторонній трикутник зі стороною AB=BC=AC=12.
Бічні грані цієї призми – рівні прямокутники, оскільки бічні ребра призми (висота призми) – паралельні й рівні.
Площину проведемо через сторону AB основи призми та точку C1.
В результаті перетину заданої призми площиною в перерізі утвориться трикутник ABC1, сторони AC1 і BC1 якого є діагоналями бічних граней.
Оскільки бічні грані правильної призми рівні, то AC1=BC1, тому ΔABC1 – рівнобедрений з основою AB=12.
Розглянемо бічну грань BB1C1C.
З прямокутного трикутника BCC1 (∠BCC1=90) за теоремою Піфагора знайдемо гіпотенузу BC1 – довжину діагоналі бічної грані (тут BC=12 і CC1=6 – катети):
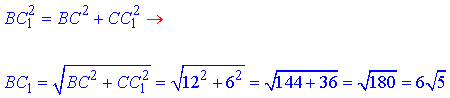
Розглянемо рівнобедрений ΔABC1, у якого AB=12 та AC1=BC1=6√5.
З вершини C1 трикутника ABC1 проведемо медіану C1M, тоді AM=MB=6.
За властивістю рівнобедреного трикутника C1M – висота і бісектриса, тому ∠C1MB=90.
З прямокутного трикутника C1MB (∠C1MB=90) за теоремою Піфагора знайдемо катет C1M – висоту рівнобедреного ΔABC1:
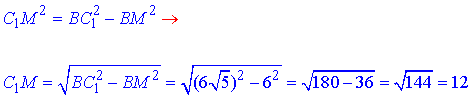
Знайдемо площу ΔABC1:
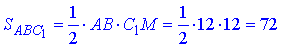
Відповідь: 72.
Задача 36.31 Периметри двох граней правильної трикутної призми дорівнюють 48 см і 30 см. Знайти об'єм V призми у кубічних сантиметрах.
У відповідь записати V/√3.
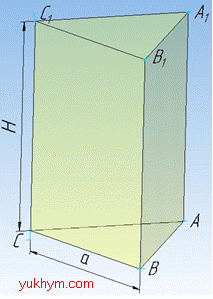
Розв'язання: Об'єм правильної призми обчислюють за формулою V=Sос•H.
В основі правильної трикутної призми лежать 2 рівних рівносторонніх трикутники ABC зі стороною AB=BC=AC=a.
Бічні грані правильної трикутної призми – рівні прямокутники, сторонами якого є сторони основи a і бічні ребра (висота) призми H.
Тому периметри граней призми, що задані в умові – це периметр основи і бічної грані правильної трикутної призми, оскільки вони мають різні значення (а периметри рівних фігур – рівні). Якби периметр основи дорівнював 48, то периметр бічної грані не міг би дорівнювати 30, оскільки:
Poc=3a'=48, звідси a'=16, а
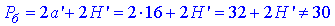
Отже, Pос=PABC=3a=30, звідси a=10 – сторона основи правильної призми.
Pб=2a+2H=20+2H=48, 2H=28, звідси H=14 – висота (довжина бічного ребра) правильної трикутної призми.
Площа основи (правильного трикутника ABC) зі стороною a=10:
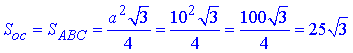
Об'єм правильної трикутної призми:
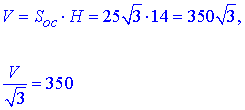
Відповідь: 350.
Далі наведені відповіді до прикладів на чотирикутні призми.



