Задачі на похилу призму одні із найважчих, оскільки вимагають доброго знання кутів, а саме формул синусів косинусів та інших тригонометричних співвідношень. Без їх знань подібних задач Вам не розв'язати, оскільки тут ще потрібно знаходити висоти, площі та об'єми. Бокові грані можуть мати форму ромбів та паралелограмів, тому такого сорту приклади фактично охоплюють весь курс геометрії за 10-11 клас. Наведені приклади взято із посібника для ЗНО підготовки, тому з однієї сторони вони дещо важчі ніж привичні шкільні завдання, з іншої - з них більше користі для самопідготовки до ВУЗ-ів.
Пропонуємо завантажити відповіді (Посібник для підготовки до зовнішнього незалежного тестування з математики).
Автори: Анатолій Капіносов, Галина Білоусова, Галина Гап'юк, Сергій Мартинюк, Лариса Олійник, Петро Ульшин, Олег Чиж
Тема 36.2 Похила призма
Задача 36.11 Основою похилої призми є паралелограм зі сторонами 6 см і 3 см і гострим кутом 450. Бічне ребро призми дорівнює 4 см і нахилене до площини основи під кутом 300. Знайти об’єм призми.
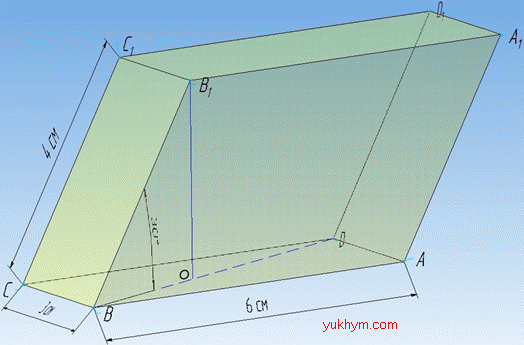
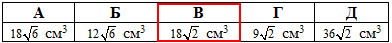
Розв'язання: Об’єм похилої призми:
V=Soc•H, де Soc – площа основи, паралелограма ABCD;
H=B1O – висота похилої призми.
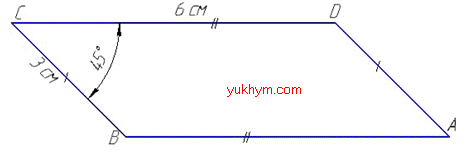
Площа основи, паралелограма ABCD (BC=AD=3 см, CD=AB=6 см, ∠BCD=45):
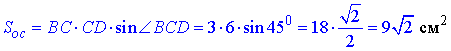
У похилої призми знайдемо висоту B1O, B1O⊥BO, де BO – проекція похилої (бічного ребра BB1) на площину ABC (відрізок BO, який належить грані ABCD), тому кут між бічним ребром і площиною:
∠B1BO=30.
У прямокутному трикутнику B1OB (∠B1OB=90) відомо:
(∠B1BO=30, B1B=4 см (у призми бічні ребра паралельні і рівні) – гіпотенуза ΔB1OB.
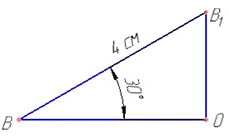
За означенням синуса гострого кута прямокутного трикутника знайдемо протилежний катет B1O до ∠B1BO – висоту призми:
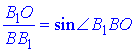
звідси
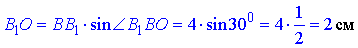
Об’єм похилої призми:
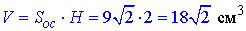
Відповідь: 18√2 см3 – В.
Задача 36.12 Бічне ребро похилої чотирикутної призми дорівнює 12 см, а перпендикулярним перерізом є ромб зі стороною 5 см. Знайти площу бічної поверхні призми.
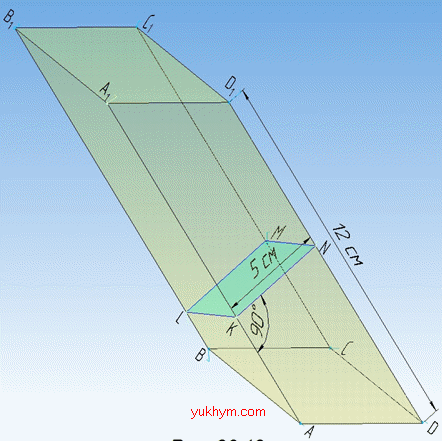
Розв'язання: Площа бічної поверхні похилої призми:
Sb=Pper•DD1, де Pper – периметр перерізу KLMN, перпендикулярного до бічного ребра; AA1=BB1=CC1=DD1=12 см – довжина бічного ребра похилої призми.
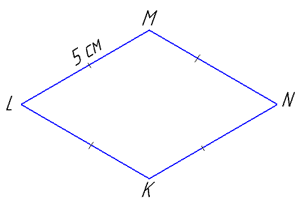
Периметр перерізу KLMN, перпендикулярного до бічного ребра:
Pper =4a=4•5=20 см,
де a=KL=LM=MN=NK=5 см – сторона ромба.
Площа бічної поверхні похилої призми:
Sb=Pper•DD1=20•12=240 см2.
Відповідь: 240 см2 – Г.
Задача 36.32 Знайти у кубічних сантиметрах об'єм похилої трикутної призми, якщо відстані між її бічними ребрами дорівнюють 3,7 см, 1,3 см і 3 см, а площа бічної поверхні – 480 см2.
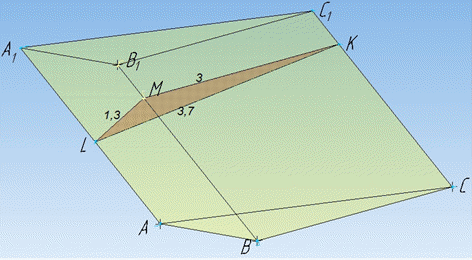
Розв'язання: Об'єм похилої трикутної призми обчислюють за формулою:
V=Sпер•AA1, де Sпер=SKLM – площа перерізу, перпендикулярного до бічного ребра AA1.
Відстань між прямими – спільний перпендикуляр до цих прямих, тому відстані між бічними ребрами похилої призми в умові задачі – це довжини відрізків перпендикулярного перерізу (довжини сторін ΔKLM):
KL=3,7 см; KM=3 см; LM=1,3 см.
За формулою Герона знайдемо площу ΔKLM:
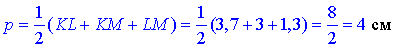– півпериметр ΔKLM;
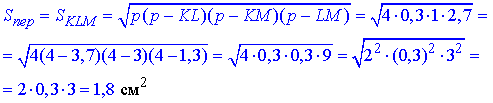– площа ΔKLM.
Площа бічної поверхні похилої трикутної призми обчислюють за формулою:
Sб=Pпер•AA1, де Pпер=2p=8 см – периметр перерізу, перпендикулярного до бічного ребра AA1, тобто периметр ΔKLM.
480=8•AA1, звідси отримаємо AA1=60 см – довжина бічного ребра.
Об'єм похилої трикутної призми:
V=Sпер•AA1=1,8•60=108 см3
Відповідь: 108
Задача 36.33 Основою похилого паралелепіпеда є ромб зі стороною 4 см і гострим кутом 600. Бічне ребро паралелепіпеда дорівнює 4 см й утворює з ребрами основи, які виходять з цієї ж вершини, кути 450.
Знайти об'єм паралелепіпеда у кубічних сантиметрах.
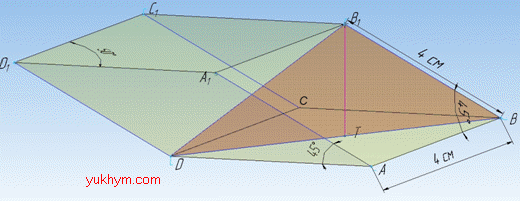
Розв'язання: Об'єм похилого паралелепіпеда обчислюють за формулою:
V=Soc•H, де Soc=SABC – площа основи паралелепіпеда (ромба ABCD);
H – висота паралел.
Знайдемо площу ромба ABCD (за двома сторонами і кутом між ними):
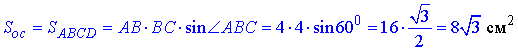
Оскільки бічні ребра похилого паралелепіпеда нахилені під однаковим кутом 450 до площини основи, то висота B1T=H проектується на діагональ BD основи (ромба ABCD).
За властивістю ромба:
діагоналі є бісектрисами його кутів.
Тому ∠ABD=30, ∠B1AB=45 (за умовою задачі), і нехай ∠B1BD=phi – кут між бічним ребром B1B і площиною основи (відрізком BT).
За теоремою косинусів тригранного кута маємо співвідношення:
звідси
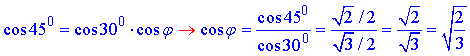
Отримаємо
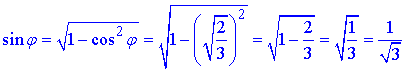
Розглянемо прямокутний трикутник BB1T (∠BTB1=90), у якого BB1=4 см – гіпотенуза, sin(phi)=1/√3 – кут, що лежить проти відрізка B1T.
За означенням синуса гострого кута прямокутного трикутника знайдемо катет (висоту призми) B1T: звідси
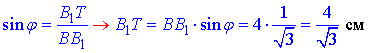
Об'єм похилого паралелепіпеда:
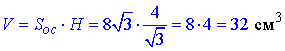
Відповідь: 32 см3
Задача 36.35 Основою призми є правильний трикутник зі стороною 4. Одна з бічних граней перпендикулярна до основи і є ромбом, діагональ якого дорівнює 6.
Знайти об'єм V призм. У відповідь записати V√21.
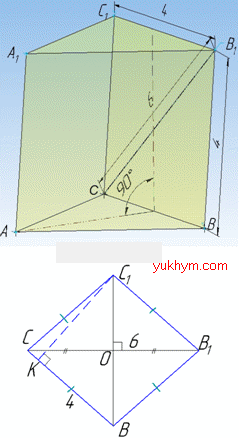
Розв'язання: Об'єм трикутної призми обчислюють за формулою:
V=Soc•H, де Soc=SABC – площа основи призми (трикутника ABC) ;
H – висота призми.
За умовою задачі, основа призми – правильний (рівносторонній) трикутник зі стороною a=AB=BC=AC=4.
Площа основи (трикутника ABC):
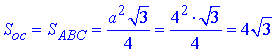
Розглянемо бічну грань (ромб BB1C1C), яка перпендикулярна до площини основи за умовою задачі.
Сторона ромба дорівнює стороні основи, оскільки відрізок BC=4 – спільний, а діагональ ромба B1C=6.
Оскільки площина ромба BB1C1C перпендикулярна до площини основи, то висота ромба C1K перпендикулярна до площини основи і є висотою призми:
H=C1K.
За властивістю ромба: діагоналі перетинаються під прямим кутом ∠BOC=90 і в точці перетину діляться навпіл B1O=OC=3, BO=OC1.
Із прямокутного трикутника BOC (∠BOC=90), в якому OC=3 – катет, BC=4 – гіпотенуза, знайдемо катет BO:
BO2=BC2-OC2, звідси
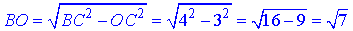
За властивістю:
BC1=2BO=2√7.
Площа ромба BB1C1C:
S=BC•C1K=B1C•BC1/2, тобто BC•C1K=B1C•BC1/2, звідси
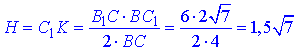
Об'єм трикутної призми рівний:
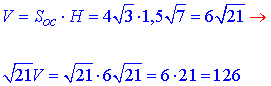
Відповідь: 126.
В наступній темі розглянемо поширені приклади на трапеції. На Вас чекають нові 35 прикладів з рисунками та поясненнями.
