Продовжуємо розбирати пояснення ЗНО тестів з математики за 2020 рік. Легші завдання проаналізовані в попередній статті. Уважно розбирайте пояснення та звертайте увагу на оформлення розв'язків.
Завдання 24. Установіть відповідність між вимірами циліндра (1– 3) та правильним щодо нього твердженням (А–Д).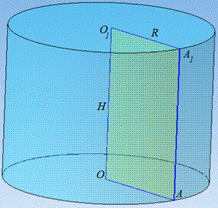
1 радіус основи дорівнює 6, висота - 4 | А циліндр утворено обертанням |
Розв'язування: 1. Маємо циліндр з розмірами R=6 - радіус основи і H=4 - висота.
Тоді AA1=H=4 - твірна циліндра. В
2. Задано циліндр з розмірами R=2 - радіус основи і H=6 - висота.
Тоді площу бічної поверхні циліндра знайдемо за формулою
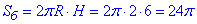 Г
Г
3. Маємо циліндр з розмірами R=4 - радіус основи і H=6 - висота. Тоді циліндр утворено обертанням прямокутника AA1O1O зі сторонами AO=A1O1=4 та AA1=OO1=6 навколо більшої сторони OO1=6. А
Завдання 25. Вартість оренди автомобіля бюджетного класу складається з основної плати та додаткової плати за понаднормовий пробіг. За перевищення норми пробігу (50 км за одну добу) нараховують додаткову плату в розмірі 6 грн за кожен понаднормовий кілометр. Пробіг автомобіля, орендованого на 6 діб, становить 420 км.
1. Яку суму грошей P (у грн) становитиме додаткова плата за понаднормовий пробіг орендованого автомобіля?
2. Основна плата за оренду автомобіля є фіксованою й становить 400 грн за кожну добу. Скільки відсотків від основної плати за 6 діб становить сума грошей P?
Розв'язування: 420:6=70 (км) - пробіг орендованого автомобіля за 1 добу;
70-50=20 (км) - понаднормовий пробіг автомобіля за 1 добу;
20∙6=120 (грн) - додаткова плата оренди авто за 1 добу.
1. P=120∙6=720 (грн) - додаткова плата за понаднормовий пробіг орендованого автомобіля за 6 діб.
400•6=2400 (грн) - основна плата оренди авто за 6 діб.
2. Складаємо пропорцію
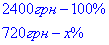
звідси рівняння
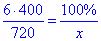
тоді
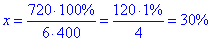
Отже, 30% від основної плати за 6 діб становить сума грошей P.
Відповідь: 720; 30%.
Завдання 26. На рисунку зображено прямокутник ABCD та два кола, що мають зовнішній дотик.
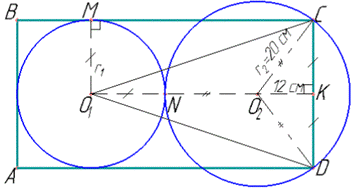
Коло із центром у точці O1 дотикається сторін AB, BC та AD, а коло із центром у точці O2 проходить через вершини C та D. Відстані від точки O2 до вершини C та сторони CD дорівнюють 20 см і 12 см відповідно.
1. Визначте радіус меншого кола (у см).
2. Обчисліть площу трикутника DO1C (у см2).
Розв'язування: За умовою задачі маємо:
O2C=r2=20 см - відстань від центра кола O2 до вершини C, радіус більшого кола;
O2K=12 см - відстань від точки O2 до сторони CD (O2K⊥CD).
N - точка дотику двох кіл, тому O2N=r2=20 см;
O1N=r1- радіус меншого кола; точки O1, N, O2 і K лежать на одній прямій (O1K⊥CD).
У прямокутному ΔO2KC (∠O2KC=90) за теоремою Піфагора знайдемо катет CK:
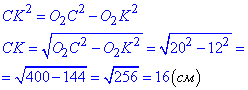
1. CK=O1M=O1N=r1=16 см - радіус меншого кола (з центром у точці O1).
2. Площа трикутника DO1C:
SΔDO1C=1/2•O1K•CD, де CD=2•CK=2•16=32 (см) - основа рівнобедреного ΔDO2C (O2C=O2D=r2), тому відрізок O2K - висота, бісектриса і медіана у ΔDO2C;
O1K=O1N+O2N+O2K=r1+r2+O2K=16+20+12=48 (см).
Обчислюємо площу
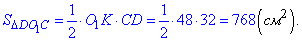
Відповідь: 16; 768.
Завдання 27. Розв'язування В арифметичній прогресії (an) відомо, що a2-a5=7,8.
1. Визначте різницю d цієї прогресії.
2. Визначте перший член a1 цієї прогресії, якщо її третій член a3=-1,8.
Завдання 28. Човен проплив 18 км проти течії річки, витративши вдвічі менше часу, ніж на подолання 48 км за течією. Власна швидкість човна є сталою. Визначте власну швидкість човна (у км/год), якщо швидкість течії дорівнює 2,5 км/год.
Розв'язування: Позначимо x, км/год - власна швидкість човна;
x+2,5, км/год - швидкість човна за течією річки;
x-2,5, км/год - швидкість човна проти течії річки;
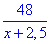 , год - час, за який проплив човен за течією річки;
, год - час, за який проплив човен за течією річки;
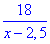 , год - час, за який проплив човен проти течії річки.
, год - час, за який проплив човен проти течії річки.
Тоді за умовою складаємо рівняння
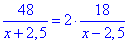 .
.
Перш ніж його обчислювати випишемо ОДЗ:
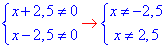
Розписуємо рівняння
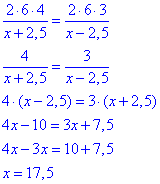
Звідси, 17,5 км/год - власна швидкість човна.
Відповідь: 17,5.
Завдання 29. У першому рядку таблиці наведено значення температури повітря, яку вимірювали на метеостанції через кожні 3 години впродовж доби. У другому рядку зазначено частоту фіксувань відповідного значення температури впродовж доби. За даними метеостанції визначте середню температуру (у 0С) протягом цієї доби.
Температура, 0С | 12 | 15 | 17 | 18 |
Частота | 1 | 4 | 2 | 1 |
Розв'язування: Середню температуру обчислимо як відношення суми температур, з урахуванням частотності, та суми частот: 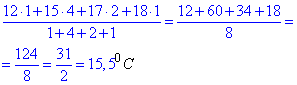 .
.
Відповідь: 15,5.
Завдання 30. Пояснення Висота правильної чотирикутної піраміди дорівнює 12 см, апофема - 13 см. Обчисліть об'єм (у см3) цієї піраміди
Завдання 31. Для участі в роботі студентської ради з кожної з двох груп навмання вибирають по 1 студенту. Серед 24 студентів першої групи проживають у гуртожитку 6 студентів, а серед 28 студентів другої групи - 14 студентів.
Яка ймовірність того, що обидва вибрані для роботи в раді студенти будуть з тих, хто проживає у гуртожитку?
Розв'язування: Нехай A - подія, яка полягає у тому, що у першій групі з 6 студентів, які проживають у гуртожитку навмання вибрали 1 студента з 24 у студентську раду, тоді ймовірність цієї події P(A) обчислюють наступним чином:
P(A)=6/24=1/4.
B - подія, яка полягає у тому, що у другій групі з 14 студентів, які проживають у гуртожитку навмання вибрали 1 студента з 28 у студентську раду, тоді ймовірність цієї події P(B) обчислюють аналогічно: P(B)=14/28=1/2.
Оскільки студентів обирають і з першої, і з другої групи, то ймовірність обчислимо як добуток ймовірностей для кожної з груп:
Відповідь: 0,125.
Завдання 32. У прямокутній системі координат Оху на площині коло задано рівнянням x2-4x+y2+12y=9. Центр O цього кола збігається з точкою перетину діагоналей паралелограма ABCD. Визначте координати вершини C(xc;yc), якщо вектор OA(-1;2). У відповідь записати добуток xc∙yc.
Розв'язування: Щоб визначити координати центра O(x0;y0) кола та його радіус R, зведемо рівняння кола до канонічного виду: 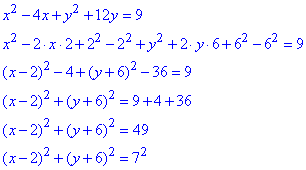
Отримали коло з центром у точці O(2;-6) і радіусом R=7. Оскільки діагоналі AC і BD паралелограма ABCD у точці перетину (точка O(2;-6)) діляться навпіл, то вектори 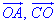 рівні, звідси CO(-1;2).
рівні, звідси CO(-1;2).
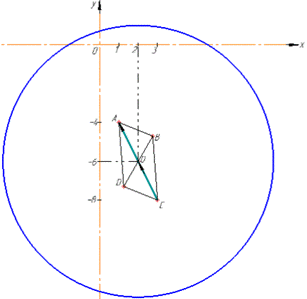
Знайдемо координати точки C(xc;yc):
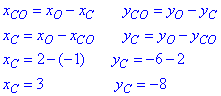
Отримали точку C(3;-8), де xc∙yc=3∙(-8)=-24.
Відповідь: -24.
Завдання 33. Задано функції f(x)=1 та g(x)=sin(x).
1. Побудуйте графік функції f.
2. Побудуйте графік функції g на проміжку [-π/2;π/2].
3. Позначте на рисунку точку, що є спільною для обох побудованих графіків функцій f і g, і запишіть її координати.
4. Знайдіть множину всіх коренів рівняння f(x)=g(x) на інтервалі (-∞;+∞).
Розв'язування: 1. Графік функції f(x)=1 є паралельним осі абсцис (Ox) і перетинає вісь ординат (Oy) у точці (0;1).
2. Графіком функції g(x)=sin(x) є синусоїда на проміжку [-π/2;π/2], яка є симетричною відносно осі ординат (функція g(x)=sin(x) непарна).
Для побудови графіка знайдемо координати деяких точок і запишемо у таблицю:
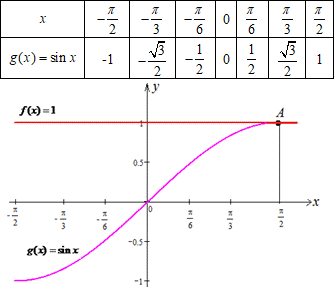
3. На рисунку та з таблиці видно, що точка A(π/2;1) є спільною для обох графіків функцій f(x)=1 та на g(x)=sin(x) проміжку [-π/2;π/2].
4. Розв'яжемо рівняння f(x)=g(x) на множині дійсних чисел (-∞;+∞):
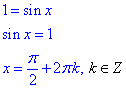
Завдання 34. Повна відповідь У прямокутному паралелепіпеді ABCDA1B1C1D1 через сторону AD нижньої основи та середину ребра B1C1 проведено площину γ. Висота паралелепіпеда дорівнює 18, грань CC1D1D є квадратом. Діагональ паралелепіпеда утворює з площиною основи кут α.
1. Побудуйте переріз паралелепіпеда ABCDA1B1C1D1 площиною γ.
2. Укажіть вид перерізу та обґрунтуйте свій висновок.
3. Визначте площу перерізу.
Завдання 35. Задано рівняння 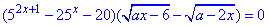 , де x - змінна, a - стала.
, де x - змінна, a - стала.
1. Розв'яжіть рівняння 5^(2x+1)-25^x-20=0
2. Розв'яжіть задане рівняння залежно від значень a.
Розв'язування: 1. Розпишемо показникове рівняння:
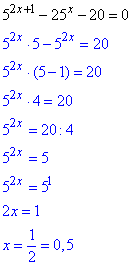
2. Розв'яжемо перше рівняння залежно від значень параметра a. 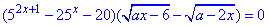
ОДЗ: 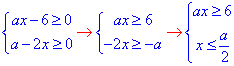
Рівняння розпадається на два рівняння:
а) 5^(2x+1)-25^x-20=0;
б) 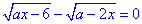 .
.
x=1/2 - корінь рівняння 5^(2x+1)-25^x-20=0.
Підставимо його в ОДЗ і знайдемо значення a, за яких цей корінь може існувати:
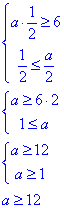
Отже, при a∈[12;+∞) маємо x=1/2 розв'язок заданого рівняння. Розв'яжемо рівняння
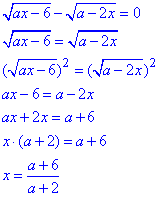
Підставимо отриманий розв'язок в ОДЗ і знайдемо значення a, за яких цей корінь може існувати:
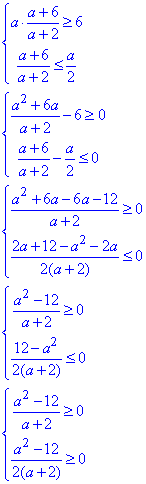
Обидві нерівності останньої системі є еквівалентними, тому
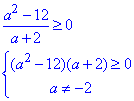
Розв'яжемо рівняння
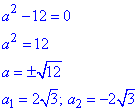
Отже, 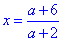 є розв'язком рівняння, якщо параметр належить 2 інтервалам
є розв'язком рівняння, якщо параметр належить 2 інтервалам
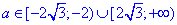 .
.
Запишемо усі розв'язки рівняння 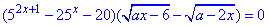 залежно від значень параметра a:
залежно від значень параметра a:
якщо 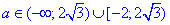 , то рівняння коренів не має;
, то рівняння коренів не має;
якщо 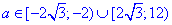 , то
, то 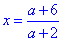 ;
;
якщо a∈[12;+∞), то x=1/2 і 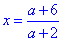 .
.
Ви можете самостійно знайти безліч онлайн ресурсів де можна пройти тестування на основі завдань підібраних зі "Збірника для тестових завдань" А. Капіносова, перевірити, що Ви вмієте та визначити, які теми Вам слід підтягнути. Додатково можете займатися як самостійно так із репетитором.
І пам'ятайте, що найкраща підготовка, це практика. Чим більше Ви пройдете завдань з цього збірника, тим сміливіше будете себе почувати на тестах.


