Основна сесія зовнішнього незалежного оцінювання з математики у 2020 році проходила 25 червня. Пропонуємо власні повні розв’язки завдань з поясненнями до обчислень.
Завдання 1. Обчислити
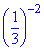
А | Б | В | Г | Д |
-9 | -1/9 | -1/6 | 1/9 | 9 |
Розв'язування: Спростимо вираз на основі властивостей степенів
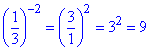
Відповідь: 9 – Д.
Завдання 2. Прямі l, m і n лежать в одній площині (див. рисунок).
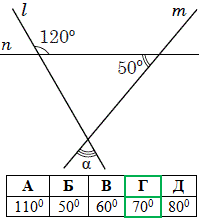
Визначте градусну міру кута α.
Розв'язування: Нехай прямі l і n перетинаються в точці A, прямі m і n - у точці B, прямі l і m - у точці C.
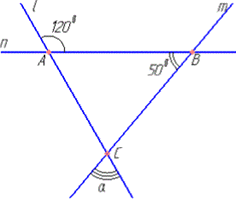
Отримали трикутник ABC, у якого ∠ABC=500 (внутрішній кут B), ∠500 (зовнішній кут).
Знайдемо внутрішній кут A, який є суміжним до кута 1200:
∠BAC=1800-1200=600.
За теоремою про суму кутів трикутника ABC знайдемо кут ACB (внутрішній кут C):
∠ACB=1800-(600+500)=1800-1100=700.
Кути ACB і α - вертикальні, а тому за теоремою рівні, отже α=∠ACB=700.
Відповідь: 700 – Г.
Завдання 3. Копіювальна машина робить 3 копії за 4 секунди. Яку максимальну кількість копій можна одержати за 1 хвилину?
А | Б | В | Г | Д |
45 | 60 | 75 | 80 | 120 |
Розв'язування: 3/4 копій може зробити машина за 1 секунду, 1 хв=60 с, тоді
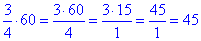
копій (за 1 хвилину).
Відповідь: 45 – А.
Завдання 4. Яке з наведених чисел є коренем рівняння 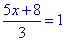 ?
?
А | Б | В | Г | Д |
1 | 0 | 3 | -2 | -1 |
Розв'язування: Перетворимо рівняння та виразимо "ікс"
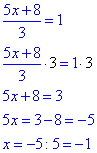
Відповідь: -1 – Д.
Завдання 5. Сума довжин усіх ребер куба дорівнює 72 см.
Визначте довжину одного ребра цього куба.
А | Б | В | Г | Д |
1 | 0 | 3 | -2 | -1 |
Розв'язування: Куб - чотирикутна пряма призма, у якої всі ребра рівні.
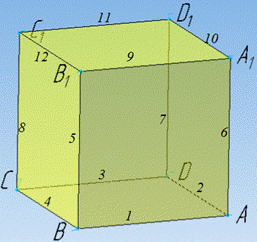
Запам'ятайте, що у куба всього 12 ребер, тому
72:12=6 (см) - довжина одного ребра.
Відповідь: 6 см – А.
Завдання 6. На рисунку зображено графік функції y=f(x) визначеної на проміжку [-2;4]. Укажіть нуль цієї функції.
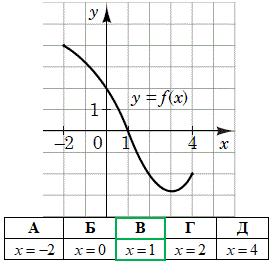
Розв'язування: Нуль функції - це точка на осі абсцис (Ox), у якій графік функції y=f(x) перетинає цю вісь, з графіка це x=1.
Відповідь: x=1 – В.
Завдання 7. Розв'яжіть рівняння x^2-4x+3=0.
А | Б | В | Г | Д |
1 | 0 | 3 | -2 | -1 |
Розв'язування: Квадратне рівняння обчислюємо через дискримінант
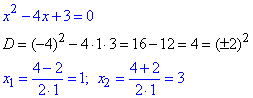
Відповідь: 1; 3 – Б.
Завдання 8. На вершину гори ведуть 5 доріг. Скільки всього є варіантів вибору маршруту підйому на вершину гори однією дорогою, а спуску іншою?
А | Б | В | Г | Д |
5 | 9 | 10 | 20 | 25 |
Розв'язування: При підйомі на гору можна вибрати 5 різних варіантів, тобто m=5;
при спуску з гори лишається вибрати вже з 4 інших маршрутів, тобто n=4. Загальна кількість варіантів сходження на гору і спуску з гори різними шляхами є добутком (оскільки сходження і спуск пов'язані сполучником "і") m=5 і n=4, тобто m•n=5∙4=20.
Відповідь: 20 – Г.
Завдання 9. Які з наведених тверджень є правильними?
І. Діагоналі будь-якого ромба ділять його кути навпіл.
ІІ. Діагоналі будь-якого чотирикутника точкою перетину діляться навпіл.
ІІІ. Діагоналі будь-якого квадрата перпендикулярні.
А | Б | В | Г | Д |
лише І | І, ІІ та ІІІ | лише ІІІ | лише І та ІІ | лише І та ІІІ |
Розв'язування: Твердження І і ІІІ є властивостями ромба (а також квадрата, як різновиду ромба), тому вони є правильними.
Твердження ІІ є неправильним, оскільки чотирикутник не має такої властивості і далеко не у всіх чотирикутників діагоналі у точці перетину діляться навпіл.
Відповідь: лише І та ІІІ – Д.
Завдання 10. На якому з рисунків зображено ескіз графіка функції 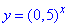 ?
?
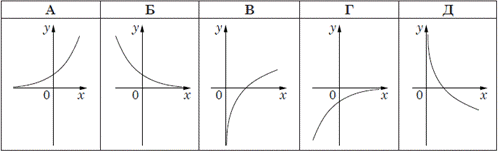
Розв'язування: Графік функції y=0,5^x спадає на всій області визначення і має область значень E(y)=(0;+∞), причому y(0)=(0,5)0=1, тобто (0;1) - точка перетину графіка функції y=0,5^x з віссю ординат (Oy).
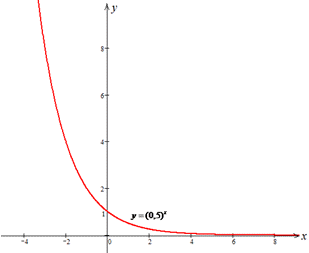
Робимо висновок, що ескіз графіка функції y=0,5^x є на рисунку Б.
Відповідь: Б.
Завдання 11. Радіус основи конуса дорівнює r, твірна - l. Твірна утворює з висотою конуса кут 600 (див. рисунок). Визначте r/l.
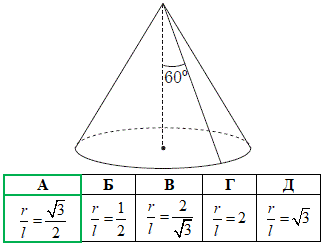
Розв'язування: Маємо конус з твірною SA=l, радіусом основи AO=r і ∠ASO=60 – кут між твірною SA=l і висотою (за умовою задачі).
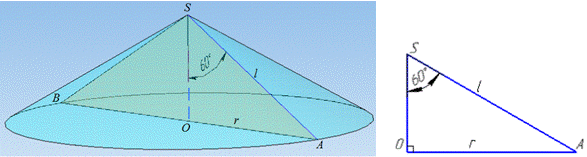
Розглянемо прямокутний ΔAOS (∠AOS=900), в якому SA=l – гіпотенуза і ∠ASO=600 – кут, що є протилежним до катета AO=r.
За означенням синуса гострого кута прямокутного трикутника знайдемо відношення r/l:
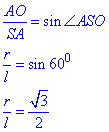
Відповідь: r/l=√3/2 – А.
Завдання 12. Розкладіть вираз (x+y)^2-9x^2 на множники.
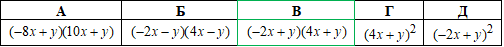
Розв'язування: Застосовуємо формулу різниці квадратів
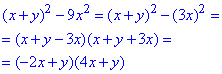
Відповідь: (-2x+y)(4x+y) – В.
Завдання 13. Графік довільної функції y=f(x) паралельно перенесли вздовж осі y на 3 одиниці вниз.
Графік якої з наведених функцій отримали?
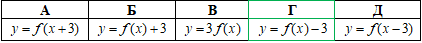
Розв'язування: Графік функції y=f(x) паралельно перенесемо вздовж осі y на a одиниць вниз і отримаємо графік функції y=f(x)-a.
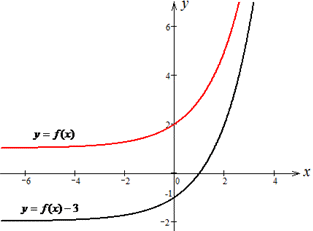
При a=3 маємо y=f(x)-3.
Відповідь: y=f(x)-3 – Г.
Завдання 14. Спростіть вираз
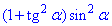
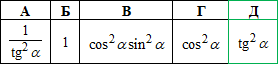
Розв'язування: Перетворимо тригонометричний вираз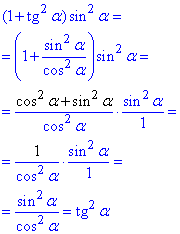 .
.
Відповідь: tg2a – Д.
Завдання 15. Розв'яжіть систему нерівностей
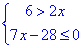
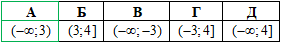
Розв'язування: Виразимо змінну з першої та другої нерівностей
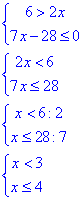

звідси x∈(-∞;3).
Відповідь: (-∞;3) – А.
Завдання 16. Укажіть проміжок, якому належить корінь рівняння
log64x=1/2.

Розв'язування: За властивістю логарифма перетворимо праву сторону та розкриємо рівняння
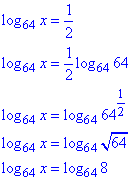
x=8, звідси x∈(6;32).
Відповідь: (6;32) – Г.
Завдання 17. Скільки всього цілих чисел містить інтервал (√8;√81)?
А | Б | В | Г | Д |
8 | 7 | 6 | 5 | 4 |
Розв'язування: Оскльки коренева функція y=√x зростає на всій області визначення, то √4<√8<√9, тобто 2<√8<3 і √81=9.
Звідси випливає, що інтервал (√8;√81) містить наступні цілі числа:
3; 4; 5; 6; 7; 8.
Тобто всього 6 цілих чисел.
Відповідь: 6 – В.
Завдання 18. На рисунку зображено прямокутник і трикутник, що є гранями правильної трикутної призми. Периметр цього прямокутника дорівнює 38 см. Визначте площу основи цієї призми, якщо довжина висоти призми дорівнює 11 см.
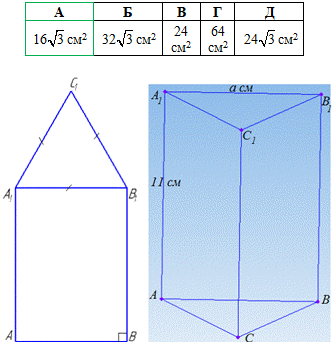
Розв'язування: Маємо прямокутник AA1B1B, у якого
AA1=11 см (висота призми),
PAA1B1B=38 см - периметр,
A1B1=a - інша сторона прямокутника і сторона правильного трикутника A1B1C1 (сторона основи призми).
Знайдемо її:
PAA1B1B=2∙(AA1+A1B1), тоді
2∙(11+a)=38,
11+a=19,
a=8 см.
A1B1=AB=8 см - довжина сторони основи призми.
Оскільки A1B1C1 - правильний (рівносторонній) трикутник, то
∠A1=∠B1=∠C1=60 і A1B1=B1C1=A1C1=a=8 см.
Знайдемо площу основи:
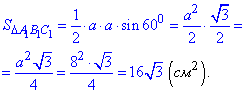
Відповідь: 16√3 см2 – А.
Завдання 19. Каркас колеса огляду складається з двох однакових кіл, до яких прикріплені 18 кабінок на однаковій відстані одна від одної, та ребер (радіусів кіл), що з'єднують місця прикріплення кабінок та центри кіл (див. рисунок). Довжина кожного ребра дорівнює 27 м. Визначте довжину дуги AB кола із центром у точці O. Укажіть відповідь найближчу до точної. Товщиною каркасу знехтуйте.
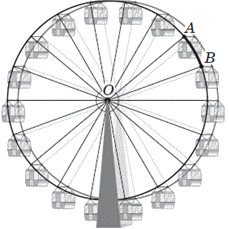
Розв'язування: Зробимо математичну модель задачі. Маємо коло з центром O і радіусом r=27 м.
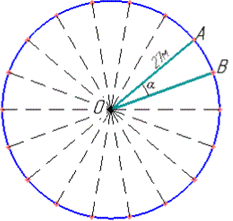
Коло розбито точками на 18 рівних частин, серед них точки A і B.
Тоді маємо
alpha=∠AOB=3600:18=200 - величина центрального кута.
Знайдемо довжину l дуги AB:
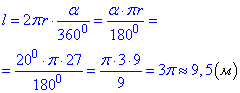
Відповідь: 9,5м – Б.
Завдання 20. Функція F(x)=5x^4-1 є первісною функції f(x). Укажіть функцію G(x), яка також є первісною функції f(x).

Розв'язування: Дві функції F(x) й G(x), які є первісними від функції f(x) відрізняються лише на сталу C, тобто F(x)-G(x)=C, звідси G(x)=F(x)-C.
Шукаємо серед варіантів А-Д первісну, яка відрізняється від заданої на константу
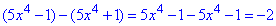
C=-2.
Записуємо первісну
G(x)=5x^4-1-(-2)=5x^4+1.
Відповідь: G(x)=5x^4+1 – Г.
Завдання 21. До кожного початку речення (1–3) доберіть його закінчення (А–Д) так, щоб утворилося правильне твердження.

Розв'язування: Побудуємо графіки заданих функцій.
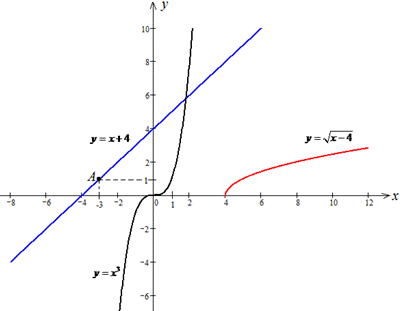
1. 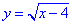 .
.
ОДЗ кореня квадратного:
x-4≥0, тобто x≥4.
Але x=1 Отже, функція 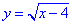 не визначена в точці x=1. Б
не визначена в точці x=1. Б
2. y(x)=x+4, тоді y(-3)=-3+4+1>0.
Графік функції y=x+4 проходить через точку A(-3;1).
Функція y=x+4 набуває додатного значення в точці x=-3. Г
3. y(x)=x^3, тоді y(-x)=(-x)^3=-x^3=-y(x).
Графік функції y=x^3 симетричний відносно початку координат. Тому функція y=x^3 є непарною. Д
Завдання 22. Установити відповідність між виразом (1– 3) та тотожно рівним йому виразом (А–Д), якщо a - довільне від'ємне число.
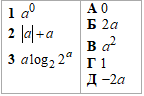
Розв'язування: За умовою маємо:
a<0.
Тоді виконуємо тотожні перетворення
1. a^0=1. Г
2. |a|+a=-a+a=0. А
3. 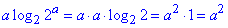 . В
. В
Завдання 23. Бічні сторони AB та CD прямокутної трапеції ABCD дорівнюють 6 см і 10 см відповідно. Менша діагональ трапеції лежить на бісектрисі її прямого кута (див. рисунок).
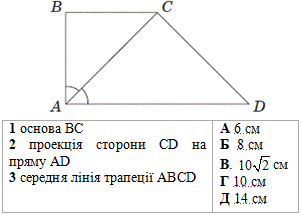
Установіть відповідність між відрізком (1–3) та його довжиною (А–Д).
Розв'язування: 1. Оскільки ∠BAC=∠CAD (AC - бісектриса) і ∠BCA=∠CAD (внутрішні односторонні кути), то ∠BAC=∠BCA.
Звідси, ΔABC - рівнобедрений BC=AB, прямокутний.
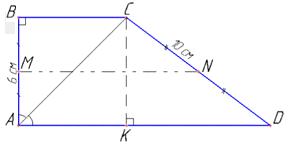
Отже, BC=6 см - основа трапеції ABCD. А
2. У трапеції ABCD проведемо висоту CK до сторони AD (CK⊥AD), тоді CK=AB=6 см (оскільки трапеція прямокутна). Відрізок KD - проекція сторони CD на пряму AD.
У прямокутному ΔCKD (∠CKD=900), у якого CD=10 см - гіпотенуза і CK=6 - катет, за теоремою Піфагора знайдемо інший катет KD:
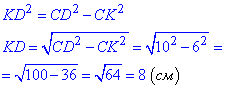 Б
Б
3. У прямокутній трапеції ABCD чотирикутник ABCK - квадрат, тому AK=BC=6 см, тоді AD=AK+KD=6+8=14 см - більша основа трапеції ABCD.
Відрізок MN - середня лінія трапеції ABCD, знайдемо її довжину:
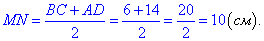 Г
Г
Практично усі теми зі Збірника тестових завдань А. Капіносова Ви можете переглянути на сторінках сайту. Більшість з низ містить категорія "Математика".
Решта готових розв'язків на тестові завдання під номерами 24-35 читайте в наступній публікації.


