Задачі на паралелепіпед з відповідями

Продовжуємо аналізувати готові приклади на призми і сьогодні пригадаємо все, що потрібно знати про паралелепіпеди. Означення, що таке паралелепіпед і його основні властивості тут давати не будемо. Це ви повинні знати із шкільних матеріалів, тут лише наведемо потрібні залежності для паралелепіпедів, які необхідні для обчислення наведених задач.
Завдання принесуть в першу чергу користь учням 10-11 класів та абітурієнтам, що готуються проходити ЗНО тестування. 
Для батьків та вчителів даний матеріал також є корисним.

Пропонуємо завантажити відповіді (Посібник для підготовки до зовнішнього незалежного тестування з математики).
Автори: Анатолій Капіносов, Галина Білоусова, Галина Гап'юк, Сергій Мартинюк, Лариса Олійник, Петро Ульшин, Олег Чиж

 

Тема 36.2 Паралелепіпед

Задача 36.4 Знайти діагональ прямокутного паралелепіпеда, виміри якого дорівнюють 2 см, 3 см і 6 см.


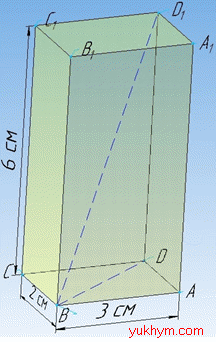
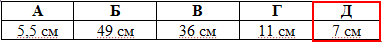
Розв'язання: Всі грані прямокутного паралелепіпеда є прямокутники.
Нехай довжини ребер паралелепіпеда дорівнюють a=2 см, b=3 см і c=6 см, тоді діагональ BD₁ прямокутного паралелепіпеда обчислюють за формулою:
(ця формула виводиться із прямокутних трикутників BAD і BDD₁)

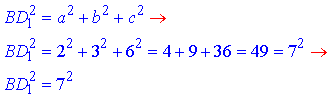
Відповідь: 7 см – Д.

ЗНО 2020. Завдання 34. У прямокутному паралелепіпеді ABCDA1B1C1D1 через сторону AD нижньої основи та середину ребра B1C1 проведено площину γ. Висота паралелепіпеда дорівнює 18, грань CC1D1D є квадратом. Діагональ паралелепіпеда утворює з площиною основи кут α.
1. Побудуйте переріз паралелепіпеда ABCDA1B1C1D1 площиною γ.
2. Укажіть вид перерізу та обґрунтуйте свій висновок.
3. Визначте площу перерізу.
Розв'язування: 1. 2. Маємо прямокутний паралелепіпед ABCDA1B1C1D1. Через сторону AD нижньої основи та середину ребра B1C1 (точка M1) проведемо площину γ.

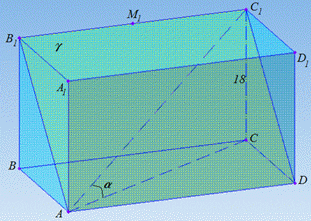
Оскільки B1C1||AD, то через прямі B1C1 і AD можна провести єдину площину, так як M1∈B1C1, то цією площиною є γ. Отже, площина γ проходить через точки A, B1, C1, D, M1, з'єднаємо послідовно ці точки і отримаємо чотирикутник AB1C1D.
Оскільки у прямокутного паралелепіпеда ABCDA1B1C1D1 протилежні грані рівні й паралельні (є прямокутниками), то AB1||C1D і B1C1||AD, тому чотирикутник AB1C1D - паралелограм (AB1=C1D і B1C1=AD).
У прямокутного паралелепіпеда ABCDA1B1C1D1 грані CC1D1D і ABCD перпендикулярні, тому CC1⊥CD і AD⊥CD.
Відрізок CC1 - перпендикуляр, CD - проекція похилої C1D на площину основи ABCD, тоді за теоремою про три перпендикуляри C1D⊥AD. Отже, ∠ADC1=90 і тому AB1C1D - прямокутник (якщо у паралелограма хоча б один з кутів прямий, то він прямокутник).

3. Площа прямокутника AB1C1D:
S_AB1C1D=AD•C1D.
Знайдемо сторони AD і C1D.
За умовою грань CC1D1D є квадратом і висота паралелепіпеда ABCDA1B1C1D1 дорівнює 18, тому CC1=CD=18.
У прямокутному трикутнику C1CD (∠C1CD=90⁰), у якого CC1=CD=18 - катети, за теоремою Піфагора знайдемо гіпотенузу C1D: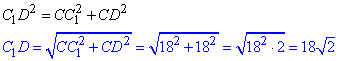
У прямокутного паралелепіпеда ABCDA1B1C1D1 діагональ AC1 утворює кут α з площиною основи ABCD (за умовою). Оскільки CC1 - перпендикуляр, то AC - проекція похилої AC1 на площину основи ABCD, звідси ∠C1AC=α.
У прямокутному трикутнику ACC1 (∠ACC1=90⁰), у якого CC1=18 - катет протилежний до кута ∠C1AC=α, за означенням тангенса гострого кута прямокутного трикутника знайдемо прилеглий катет AC:

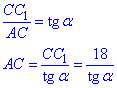
Відрізок AC - діагональ прямокутника ABCD.
У прямокутному трикутнику ADC (∠ADC=90⁰), у якого CD=18 - катет і AC=18/tg(α) - гіпотенуза, за теоремою Піфагора знайдемо катет AD:

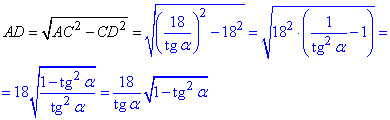
Підставимо в формулу площі прямокутника AB1C1D:

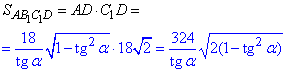
Після деяких тригонометричних перетворень площа прямокутника AB1C1D може бути записана у вигляді:

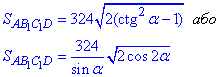
Задача 36.5 Сторони основи прямокутного паралелепіпеда дорівнюють 5 см і 12 см, а діагональ паралелепіпеда нахилена до площини основи під кутом 45⁰.
Знайти бічне ребро паралелепіпеда.


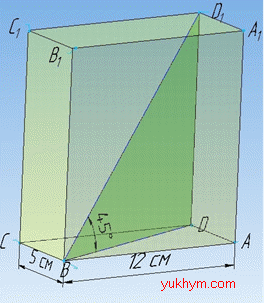
Розв'язання: Кожна грань прямокутного паралелепіпеда є прямокутником.
Тому у прямокутного паралелепіпеда кожне бічне ребро перпендикулярне до площини основи, а отже (за властивістю) і до кожної прямої, що належить площині основи.
Звідси слідує, що DD₁⊥BD, тобто ∠BDD₁=90.
Ортогональною проекцією діагоналі BD₁ прямокутного паралелепіпеда є діагональ основи BD.
Тому кут між діагоналлю BD₁ і площиною основи (грані ABCD) є кут DBD₁, тобто ∠DBD₁=45.
З прямокутного трикутника ABD (∠BAD=90), в якому AB=12 см і BC=5 см – катети, за теоремою Піфагора знайдемо діагональ BD основи паралелепіпеда: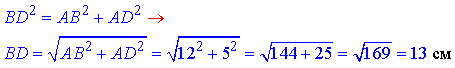
Розглянемо прямокутний трикутник BDD₁ (∠BDD₁=90), в якому BD=13 см – прилеглий катет до ∠DBD₁=45.
За означенням тангенса гострого кута прямокутного трикутника знайдемо бічне ребро DD₁ паралелепіпеда:

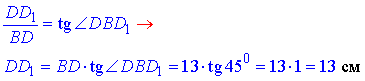
Відповідь: 13 см – Б.

Задача 36.15 Основа прямого паралелепіпеда є ромб. Площі його діагональних перерізів дорівнюють S₁ і S₂.
Визначити висоту паралелепіпеда, якщо його об'єм дорівнює V.


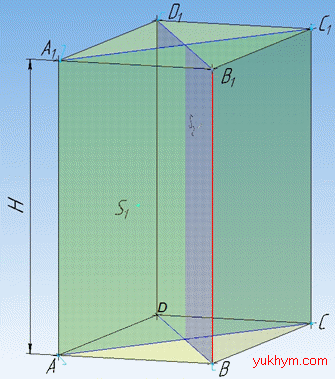
Розв'язання: Об'єм прямого паралелепіпеда:
V=Soc•H=S_ABCD•BB₁,
де Soc= S_ABCD – площа основи паралелепіпеда, тобто площа ромба ABCD;
H=AA₁=BB₁=CC₁=DD₁ – висота прямого паралелепіпеда, звідси H=V/S_ABCD.
Діагональними перерізами прямого паралелепіпеда є прямокутники, у яких дві протилежні сторони є висотами (бічними ребрами) паралелепіпеда, а дві інші діагоналями основи паралелепіпеда (ромба ABCD).

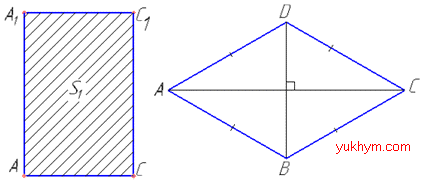
Площа I прямокутника:
SAA₁C₁C=AA₁•AC=H•AC=S₁, звідси AC=S₁/H.

Площа ІI прямокутника:
S_BB1D1D=BB₁•BD=H•BD=S₂, звідси BD=S₂/H.
Основи прямого паралелепіпеда є рівні ромби ABCD і A₁B₁C₁D₁.
Площа ромба ABCD:

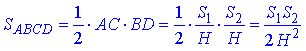
Отже, знайдемо висоту паралелепіпеда:

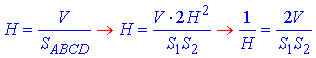
звідси отримаємо H=S₁S₂/(2V).
Відповідь: H=S₁S₂/(2V) – В.

Задача 36.19 Основою прямого паралелепіпеда є ромб, площа якого дорівнює S, а площі діагональних перерізів паралелепіпеда – S₁ і S₂.
Визначити висоту паралелепіпеда.


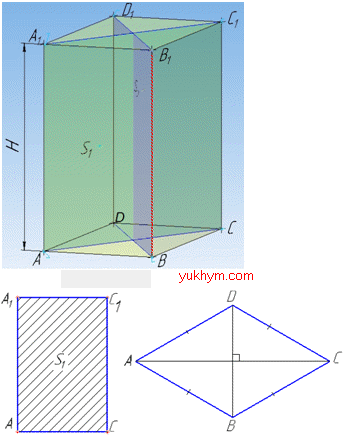
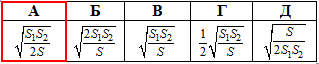
Розв'язання: Нехай Soc=S_ABCD=S – площа основи паралелепіпеда, тобто площа ромба ABCD;
H=AA₁=BB₁=CC₁=DD₁ – висота прямого паралелепіпеда.
Діагональними перерізами прямого паралелепіпеда є прямокутники, у яких дві протилежні сторони є висотами (бічними ребрами) паралелепіпеда, а дві інші – діагоналями основи паралелепіпеда (ромба ABCD).
Площа I прямокутника:

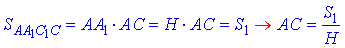
Площа ІI прямокутника:

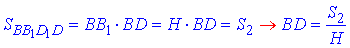
Основи прямого паралелепіпеда є рівні ромби ABCD і A₁B₁C₁D₁.
Площа ромба ABCD:

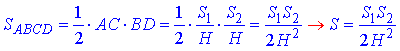
Отже, знайдемо висоту паралелепіпеда:

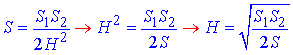
Відповідь: 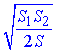– А.

Задача 36.22 Площі трьох граней прямокутного паралелепіпеда дорівнюють S1, S2 і S3.
Визначити об'єм паралелепіпеда.


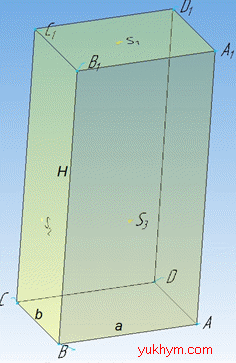
Розв'язання: Об'єм прямокутного паралелепіпеда:

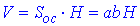
де Soc=SABCD – площа основи паралелепіпеда, тобто площа прямокутника ABCD;
H=AA₁=BB₁=CC₁=DD₁ – висота прямокутного паралелепіпеда.
Гранями прямокутного паралелепіпеда є прямокутники.
І прямокутник ABCD лежить в основі, тому його сторони AB=CD=a, AD=BC=b.
ІІ прямокутник BB₁C₁C є однією з бічних граней зі сторонами BC=B₁C₁=b, BB₁=CC₁=H.
ІІІ прямокутник ABB1A1 є також однією з бічних граней (сусідній до ІІ прямокутника) зі сторонами AB=A₁B₁=a, AA₁=BB₁=H.
За властивістю паралелепіпеда протилежні грані паралельні та рівні.
Площа I прямокутника зі сторонами a і b:

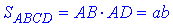
звідси S1=ab.
Площа IІ прямокутника зі сторонами H і b:

звідси S2=Hb.
Площа ІІI прямокутника зі сторонами H і a:

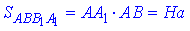
звідси S3=Ha.
Запишемо добутки лівих і правих частин останніх трьох рівностей:

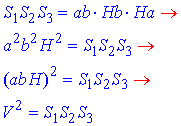
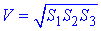– об'єм прямокутного паралелепіпеда.
Відповідь: 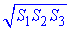– А.

Задача 36.27 Основою паралелепіпеда є ромб. Діагоналі паралелепіпеда дорівнюють 8 см і 5 см, а висота – 2 см.
Знайти у сантиметрах сторону основи.

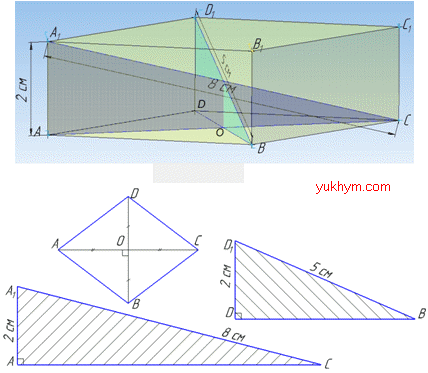
Розв'язання: Маємо паралелепіпед, в основі якого лежить ромб ABBCD;
A₁C=8 см і D₁B=5 см діагоналі паралелепіпеда;
AA₁=BB₁=CC₁=DD₁=2 см – висота паралелепіпеда.
Висота паралелепіпеда перпендикулярна до площини основи (ромба ABCD), а значить і перпендикулярна до кожного відрізка, що лежить в площині ромба, тому AA₁⊥AC і DD₁⊥BD.
Звідси слідує, що трикутники A₁AC і D₁DB – прямокутні (∠A₁AC=90 і ∠D₁DB=90).
Розглянемо прямокутні трикутники A₁AC (∠A₁AC=90) і D₁DB (∠D₁DB =90).
В них відомо: A₁A=DD₁=2 см – катети, A₁C=8 см і D₁B=5 см – гіпотенузи відповідних прямокутних трикутників.
За теоремою Піфагора знайдемо два інших катети трикутників A₁AC і D₁DB:

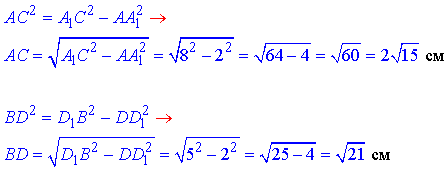
Розглянемо ромб ABCD з діагоналями AC=2√15 см і BD=√21 см.
За властивістю ромба:
діагоналі ромба перпендикулярні (AC⊥BD) і в точці перетину діляться навпіл (AO=OC=√15 см і BO=OD=√21/2 см).
Отже, трикутник AOB – прямокутний (∠AOB=90) з катетами AO=√15 см і BO=√21/2 см.
За теоремою Піфагора знайдемо гіпотенузу AB – сторону основи паралелепіпеда (ромба ABCD): AB²=AO²+BO²,

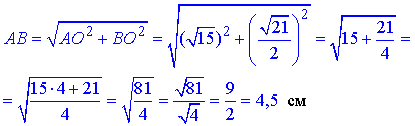
Отож, AB=BC=CD=AD=4,5 см – сторона основи паралелепіпеда.
Відповідь: 4,5 см.

Задача 36.28 Діагоналі граней прямокутного паралелепіпеда мають довжини 5, 4√10 і 3√17.
Визначити діагональ паралелепіпеда.

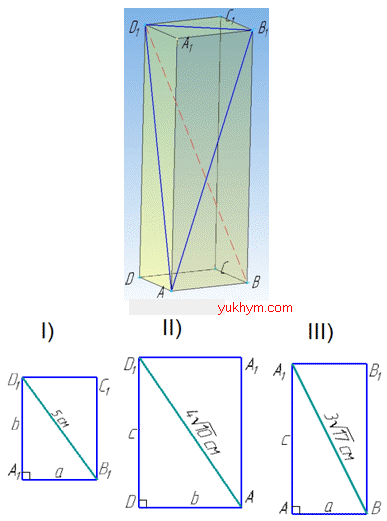
Розв'язання: Всі грані прямокутного паралелепіпеда – прямокутники.
За властивістю прямокутного паралелепіпеда – протилежні грані паралельні та рівні.
Тому розглянемо 3 прямокутники:
І) A₁B₁C₁D₁ – основа паралелепіпеда зі сторонами A₁B₁=C₁D₁=a і B₁C₁=A₁D₁=b;
діагональ грані:
(1)
ІІ) AA₁D₁D – бічна грань паралелепіпеда зі сторонами AD=A₁D₁=b і AA₁=DD₁=c;
діагональ грані:
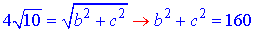(2)
ІІІ) ABB₁A₁ – бічна грань паралелепіпеда зі сторонами A₁B₁=AB=a і AA₁=BB₁=c;
діагональ грані:
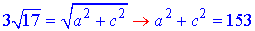(3)
Довжини діагоналей граней (прямокутників) обчислювались із відповідних прямокутних трикутників за теоремою Піфагора.
Додамо обидві частини рівностей (1), (2) і (3), отримаємо:

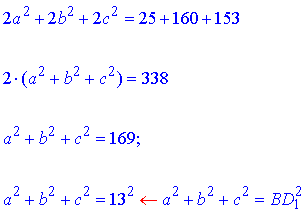
отже BD₁=13 см – довжина діагоналі прямокутного паралелепіпеда.
Відповідь: 13 см.

Задача 36.29 Визначити об'єм прямокутного паралелепіпеда, основою якого є прямокутник зі сторонами 3 і 4, а площа діагонального перерізу 20.

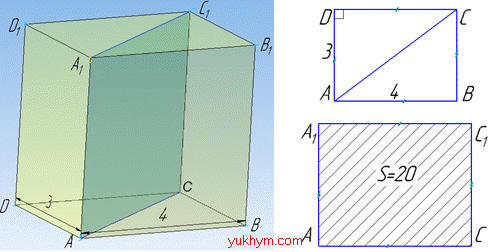
Розв'язання: Об'єм прямокутного паралелепіпеда обчислюють за формулою V=Sос•H, де Soc=S_ABCD – площа основи паралелепіпеда, тобто площа прямокутника ABCD;

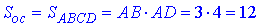
H=AA₁=BB₁=CC₁=DD₁ – висота прямокутного паралелепіпеда (довжина бічного ребра);
AD=BC=3 і AB=CD=4 – сторони основи (прямокутника) ABCD.
Діагональним перерізом прямокутного паралелепіпеда є прямокутник AA₁C₁C, сторонами якого є діагоналі основи AC і A₁C₁ (прямокутника ABCD) й бічні ребра AA₁ і CC₁ прямокутного паралелепіпеда.
Знайдемо діагональ AC із прямокутного трикутника ACD (∠ADC=90) за теоремою Піфагора:
AC²=AD²+CD², звідси

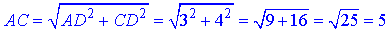
Площа діагонального перерізу (прямокутника AA₁C₁C):
S_AA1C1C=AC•AA1=5H=20,
звідси 5H=20, тобто H=4– висота паралелепіпеда.
Об'єм прямокутного паралелепіпеда:
V=Sос•H=12•4=48.
Відповідь: 48.

Задача 36.30 У прямому паралелепіпеді сторони основи 2 і 8, а кут між ними 30⁰. Бічна поверхня паралелепіпеда дорівнює 20. Визначити об'єм паралелепіпеда.

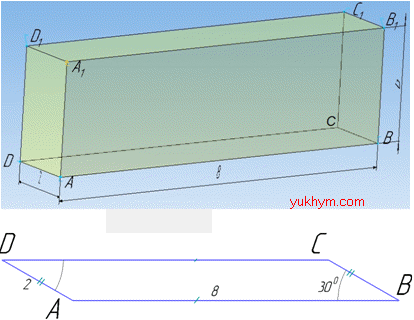
Розв'язання: Об'єм прямого паралелепіпеда обчислюють за формулою V=Sос•H, де Soc=S_ABCD – площа основи паралелепіпеда, тобто площа паралелограма ABCD:

H=AA₁=BB₁=CC₁=DD₁ – висота прямого паралелепіпеда (довжина бічного ребра);
AD=BC=2 і AB=CD=8 – сторони основи (паралелограма) ABCD;
∠ABC=∠ADC=30 – кут між сторонами основи (паралелограма) ABCD.
Бічну поверхню (тобто її площу) прямого паралелепіпеда обчислюють за формулою
S_б=Pос•H,
де Pос=P_ABCD – периметр основи паралелепіпеда:

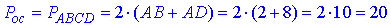
За умовою задачі S_б=Pос•H, звідси 20H=20, H=1 – висота паралелепіпеда.
Об'єм прямого паралелепіпеда:
V=Sос•H=8.
Відповідь: 8.

Якщо маєте запитання чи зауваження до наведених відповідей, тоді просимо Вас нам написати. В іншому випадку вважаємо, що матеріал Вам сподобався та був корисним. Далі розглянемо завдання на трикутні та чотирикутні призми.

Вас може зацікавити:
1. Правильна трикутна піраміда
2. Чотирикутна призма. Задачі з відповідями
3. Об'єм конуса. Тіла обертання
4. Перерізи циліндра площинами. Осьовий переріз