Скласти закон розподілу дискретної випадкової величини. M(Х), D(Х)

Сьогодні проаналізуємо готові відповіді з ТІМС, які вчать будувати закони розподілу дискретної випадкової величини Х та обчислювати числові характеристики M(X), D(X), σ(X).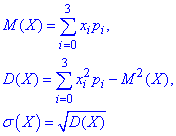

Приклад 1. Гральний кубик кидають три рази. Скласти закон розподілу випадкової величини Х – кількості появи двійки на верхній грані кубика.
Обчислити M(X), D(X) та середнє квадратичне відхилення σ.
Обчислення: Гральний кубик має 6 граней, на одній з яких 2.
Ймовірність, що випаде двійка в одному киданні рівна p1=1/6, що не випаде q1=5/6.
Закон розподілу: ймовірності, що двійка при трьох кидках випаде 0,1,2,3 рази.
p(0)=5/6^3=0,5787;
p(1)=3•1/6•5/6•5/6=0,3471;
p(2)=3•1/6•1/6•5/6=0,0693;
p(3)=1/6•1/6•1/6=0,00461.
У 2 і 3 рядках домножали на 3 за рахунок розміщень з 3 по 2 (A₃²=3!/2!).
Складаємо таблицю розподілу Х

Математичне сподівання, дисперсію та середнє квадратичне відхилення знаходимо з формул

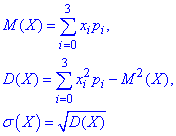
M(x)=0,5787*0+1*0,3471+2*0,0693+3*0,00461=0,01458;
D(x)=1*0,3471+4*0,0693+9*0,00461-0,01458=0,0283;
σ(X)=√D(x)=√0,0283=0,1682.
Запам'ятовуйте формули для обчислення числових характеристик дискретної випадкової величини.

Приклад 2. З дев'яти кульок, серед яких є 4 пофарбовані, навмання вибирають 5 кульок. Скласти ряд розподілу і побудувати функцію розподілу випадкової величини Х – кількості пофарбованих кульок серед вибраних.
Обчислення: Кількість пофарбованих кульок може приймати значення від 0 до їх максимальної кількості =4 серед 5, що вибирають. Оскільки "кульки" не "діти, книжки,..." і немає значення під яким номером входять в набір, а лише їх кількість то кількість всеможливих наборів визначаємо через формулу комбінацій.
Кількість різних варіантів вибрати 5 кульок з 9 рівна С₉⁵.
k – кульок з 4 пофарбованих можна вибрати С₄^k способами і лишається вибрати (5-k) непофарбованих з 5, що дорівнює С₅^5-k.
Тоді за теоремою множення ймовірностей функція розподілу рівна
p(k)=С₄^k•С₅^5-k/С₉⁵.
Для обчислення ймовірностей скористаємося математичним пакетом мейпл, в ньому за комбінації з n по m відповідає функція binomial(n,m).
Решта обчислень як і графік розподілу наведені нижче .

Зауважте, що в мейплі початковий номер має бути натуральним числом, тому зміщаємо в формулі індексна 1 вліво.
Результати записуємо в таблицю розподілу:

На основі ряду розподілу ймовірностей побудуємо функцію ймовірностей F(x).
Спершу вручну, як вимагають на практичних для студентів
F(X<0)=0;
F(0<X<1)=p(X=0)=1/126≈0,079;
F(1<X<2)=p(X=0)+p(X=1)=21/126=0,16(6);
F(2<X<3)=1/126+10/63+10/21≈0,643;
F(3<X<4)=F(2<X<3)+p(X=3)=0,643+10/63≈0,96;
F(X>4)=1.
Далі покажемо, як обчислити функцію розподілу в мейплі та побудувати її графік.

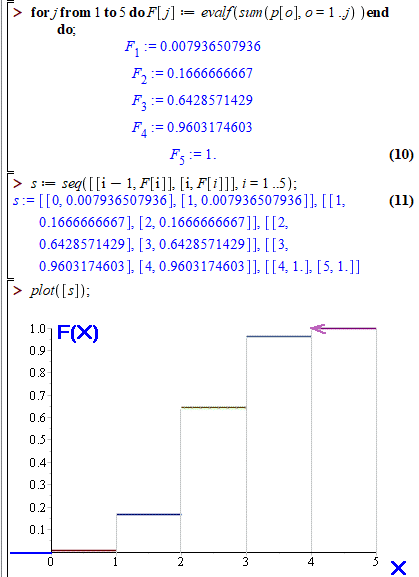
Саме такий вигляд має графік функції розподілу, іноді вимагають ставити всюди вектори як на останній ділянці.

Приклад 3. На полиці стоять 5 підручників з математики і 3 з фізики. З полиці навмання беруть три книги.
Скласти закон розподілу випадкової величини Х – кількості підручників з математики серед відібраних.
Обчислити числові характеристики M(X), D(X), σ(X).
Обчислення: Х – може приймати значення від 0 до 3. Розв'яжемо завдання двома способами.

1 спосіб

Пояснимо на пальцях усі ймовірності.
Нехай першою треба знайти ймовірність, що виберуть 0 книг з математики.
Це означає, що треба вибрати лише 3 книги з фізики з 3 серед (5+3)=8 можливих.
Ймовірність вибрати фізику першою рівна 3/8.
Після цього залишиться 8-1=7 книг, 2 з яких з фізики, тому ймовірність другою взяти фізику рівна 2/7, третьою – 1/6.
За теоремою множення ймовірностей
p(0)=3/8•2/7•1/6≈0,01786.
Ймовірність вибрати 1 підручник з математики означає 1 з 5 з математики, і 2 з 3 з фізики.
Ймовірність вибрати першим математику рівна 5/8, другим фізику – 3/7, третім фізику – 2/6.
Плюс ще треба врахувати перестановки з 3 по 1 (A31=3), оскільки математика може бути вибрана в ряді першою, другою або третьою, тобто набори
МФФ, ФМФ, ФФМ.
Обчислюємо p(1):
p(1)=3•5/8•3/7•2/6≈0,2678.
Ймовірність вийняти дві книжки з математики з 3:
ММФ, МФМ, ФММ.
Ймовірність вибрати матем. першою рівна 5/8, другою – 4/7, далі фізику – 3/6.
p(2)=3•5/8•4/7•3/6≈0,5357.
Ймовірність взяти 3 книги з 5 з математики серед 8 рівна
p(3)=5/8•4/7•3/6≈0,1786.
Тому що першою беремо одну з 5 книг серед 8, другою 1 з 4 серед 7, третьою – 1 з 3 математик з 8 книг.
Це надіюсь Вам легко усвідомити.

2 спосіб

Обчислимо через формули ймовірності. Оскільки нам неважливо яка з книг з математики чи фізики попаде в набір, а лише їх кількість, то застосовуємо формулу комбінацій. Кількість можливих способів вибрати 3 книги з 8 рівна
N=C₈³=8!/(3!•5!)=56.
Кількість способів вибрати k=0..3 книг з 5 з математики дорівнює
m₁=C₅^k=5!/(k!•(5-k)!).
3-k книг з фізики можна вибрати m2 способами
m₂=C₃^3-k=3!/(k!•(3-k)!).
Тому за теоремою множення ймовірностей
p(k)=m₁•m₂/N.
При обчисленнях отримаємо ті ж значення, що і першим способом.
Записуємо результати в таблицю закону розподілу

Це тільки пів завдання, далі обчислюємо математичне сподівання за формулою
M(x)=sum(x_i•p_i,i=0..3)=1•0,2678+2•0,5357+3•0,1786=1,626.
Формула дисперсії
M(x)=sum(x_i²•p_i,i=0..3)-M²(X)=0,6278.
Середнє квадратичне відхилення рівне кореню з дисперсії
σ(X)=√0,6278≈0,7923.
Всі числові характеристики розподілу знайдені.

Приклад 3. Ймовірність того, що покупець, який завітав до взуттєвого магазину, здійснить покупку дорівнює в середньому 0,1. Яка ймовірність того, що із 400 покупців, що завітали до магазину покупку здійснять: а) 40 покупців; б) від 50 до 80 покупців.
Обчислення: Найточніше і найшвидше розрахунки можна провести на комп'ютері з допомогою математичних пакетів, зокрема в мейплі вся відповідь має вигляд:


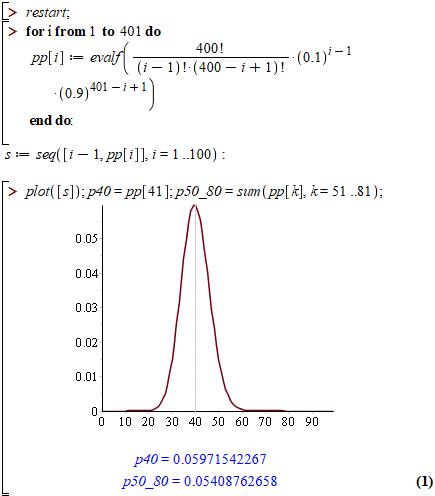
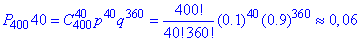
Тут Вам і закон ймовірностей, графік і шукані ймовірності в точці та на інтервалі.

На практиці колись до таких степенів ніхто не розраховував і факторіали від великих чисел не брали. Тому придумали наближені функції, якими як і 100 років тому, проведемо обчислення.
Перше значення P₄₀₀40 за локальною формулою Лапласа.
Тоді ймовірність що серед 400 людей покупку зроблять 40 рівна 0,047

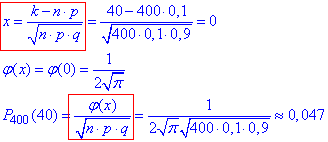
Як бачите похибка між точним значенням 0,0597 і наближеним 0,047 велика, але це вважалося нормальною збіжністю і всі наближені формули вчать по сьогодні, хоча на мою думку, такі обчислення зайві.
Далі ще інтересніше, ймовірність, що від 50 до 80 покупців за іншою – інтегральною формулою Лапласа.
Для k1=50 і k2=80 знайдемо "ікси" за формулою

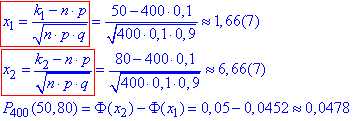
Інтегральну функцію Лапласа в точках "ікс1, ікс2" також обчислювали в мейплі.

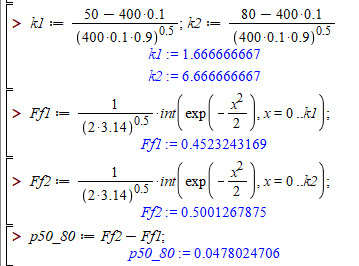
Думаю,якщо шукати онлайн таблиці інтегральної функції Лапласа, то похибка обчислень була б більшою через грубу табуляцію.
Загалом бачимо, що розходження між точним значенням 0,054 і наближеним 0,0478 досить відчутне.