Продовжуємо аналізувати практикум з теорії ймовірностей і сьогодні вивчимо характеристики вибірки - статистичний розподіл.
З сьогоднішнього уроку Ви дізнаєтесь:
що таке ранжований варіаційний ряд?
як знайти статистичні розподіли частот та відносних частот?
як будувати полігони частот і відносних частот?
що таке емпірична функція розподілу?
Всі ці поняття вивчають в курсі математичної статистики і мають пряме застосування в економіці, митній сфері, порівнянні результатів діяльності підприємств за фіксовані періоди і т.д.
Щоб не повторюватись двічі розберемо приклади на вибірки і в поясненнях наведемо означення усіх вказаних статистичних характеристик.
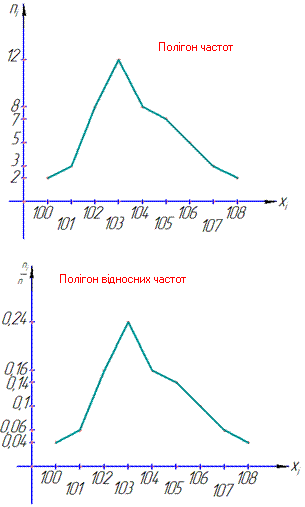
Означення: Полігон частот це ламана лінія, відрізки якої сполучають точки з координатами (xi;ni) .
Аггоритм побудови полігону частот:
на осі абсцис відкласти варіанти xi , далі на осі ординат – відповідні їм частоти ni та з'єднати їх.
Означення: Полігоном відносних частот це ламана пряма, що сполучає точки з відповідними координатами (xi;vi)
Побудова полігона відносних частот полягає в послідовному з'єднанні варіант xi в осях (xi;vi).
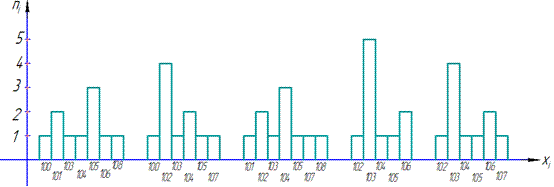
Означення: Гістограма частот це ступінчаста (східчаста) фігуру, яка має вигляд сполучених прямокутників, основа яких рівна інтервалам довжиною h, а висоти рівні відношенню ni/h (густина частоти).
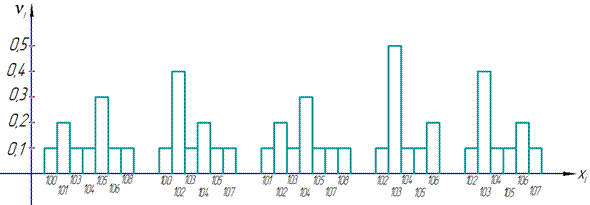
Означення: Гістограмою відносних частот це ступінчаста фігуру, подібна до гістограми частот, тільки по осі ординат відкладені густина відносних частот pi/h.
Запам'ятовувати правила, як будувати числові характеристики статистичних розподілів краще всього з готових прикладів, тому переходимо до аналізу завдань.
Приклад 1 Результати досліджень характеризуються наступними вибірками.
Необхідно побудувати:
- а) ранжований варіаційний ряд, статистичні розподіли частот і відносних частот;
- б) полігон частот і полігон відносних частот;
- в) гістограму частот і гістограму відносних частот, розбивши вибірку на 5 рівних інтервалів;
- г) записати емпіричну функцію розподілу і побудувати її графік.
106 | 101 | 104 | 105 | 100 | 108 | 105 | 103 | 101 | 105 |
100 | 102 | 107 | 103 | 102 | 105 | 102 | 102 | 104 | 104 |
104 | 108 | 102 | 102 | 101 | 105 | 104 | 103 | 107 | 104 |
103 | 106 | 105 | 103 | 102 | 104 | 103 | 103 | 106 | 103 |
103 | 107 | 102 | 104 | 106 | 106 | 103 | 103 | 105 | 103 |
Розв'язання: а) Що таке ранжований варіаційний ряд?
Варіацією називають можливість певної ознаки приймати різні значення у різних одиницях сукупності. Тому на початку статистичного дослідження варіації нообхідна побудова варіаційного ряду – упорядкування розподілу одиниць множини в порядку зростання або зменшення значень досліджуваної кількісної ознаки та знаходження числа одиниць, що рівні між собою (інтервали значень).
Виділяють три основні форми варіаційних рядів: ранжовані ряди, дискретні та інтервальні ряди.
Ранжований варіаційний ряд – це ряд впорядкованих одиниць сукупності в порядку зростання чи спадання ознаки, що досліджується.
Для заданої вибірки побудуємо ранжований ряд за зростанням
100 | 100 | 101 | 101 | 101 | 102 | 102 | 102 | 102 | 102 |
102 | 102 | 102 | 103 | 103 | 103 | 103 | 103 | 103 | 103 |
103 | 103 | 103 | 103 | 103 | 104 | 104 | 104 | 104 | 104 |
104 | 104 | 104 | 105 | 105 | 105 | 105 | 105 | 105 | 105 |
106 | 106 | 106 | 106 | 106 | 107 | 107 | 107 | 108 | 108 |
Статистичний розподіли частот і відносних частот необхідний, щоб встановити частотність входження варіанти у вибірку та визначити її долю в загальній сукупності.
Сума всіх добутків частот на відносні частоти повинна дорівнювати 1 або 100%.
Звідси знаходять частоту входження варіанти у вибірку та визначають відносну частоту за формулою
Wi=ni/n.
Результати упорядкування розподілів записуємо в таблицю
варіанта | 100 | 101 | 102 | 103 | 104 | 105 | 106 | 107 | 108 |
частота | 2 | 3 | 8 | 12 | 8 | 7 | 5 | 3 | 2 |
відносна | 0,04 | 0,06 | 0,16 | 0,24 | 0,16 | 0,14 | 0,1 | 0,06 | 0,04 |
б) Полігон частот(полігон відносних частот) – це ламані на графіку, які відображають зв'язок варіанти з їх частотою (відносною частотою).
Щоб побудувати полігон частот відкладаємо на осі абсцис значення варіант xi, а на осі ординат – частоти ni , що їм відповідають.
Така ж інструкція справедлива для полігону відносних частот Wi=ni/n).
З'єднавши точки (xi;ni) відрізками прямих, одержимо шуканий полігон частот (відносних частот):
в) Гістограма частот (вибірка розбита на 5 рівних інтервалів) - це частоти входження значень в певний інтервал.
Задана вибірка задана 50 значеннями, по 10 в кожному рядку таблиці.
Гістограма відносних частот (в кожному інтервалі по 10 елементів):
г) Емпіричну функцію розподілу визначатимемо за формулою Fn(x)=nx/n де nx – кількість елементів вибірки, що менші за x.
В результаті простих обчислень для кожного з інтервалів отримаємо значення функції Fn(x)
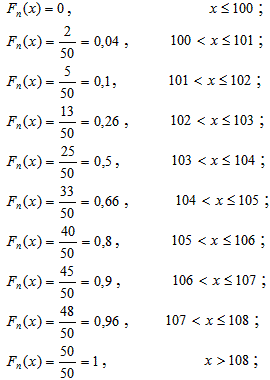
Графік емпіричної функції розподілу має вигляд:
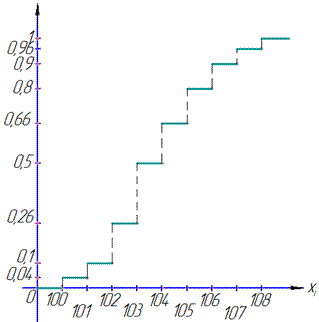
На цьому завершуються пояснення до завдання з ймовірності.
Далі наведемо ще 4 приклади на статистичний розподіл вибірки, щоб Ви краще розібралися що і для чого робимо.
Приклад 2 Результати досліджень характеризуються наступними вибірками.
Необхідно побудувати:
а) ранжований варіаційний ряд, статистичні розподіли частот і відносних частот;
б) полігон частот і полігон відносних частот;
в) гістограму частот і гістограму відносних частот, розбивши вибірку на 5 рівних інтервалів;
г) записати емпіричну функцію розподілу і побудувати її графік.
11,5 | -6 | 13 | 18 | 25,5 | 30,5 | 34,5 | 8 | 14,5 | 16 |
19,5 | 21,5 | 2 | 29 | 18,5 | 32 | -3,5 | 15,5 | 24 | 23,5 |
17 | -0,5 | 15 | 23 | 4,5 | 13,5 | 20,5 | -9 | 30 | 17,5 |
25 | 5,5 | 11 | 18,5 | 10 | 11,5 | 0,5 | 28 | 16 | 3 |
12,5 | 13 | 9,5 | 7 | 18 | 15 | 22 | 12 | 19,5 | 21 |
Розв'язання: а) Складаємо ранжований варіаційний ряд за зростанням та записуємо у вигляді таблиці:
-9 | -6 | -3,5 | -0,5 | 0,5 | 2 | 3 | 4,5 | 5,5 | 7 |
8 | 9,5 | 10 | 11 | 11,5 | 11,5 | 12 | 12,5 | 13 | 13 |
13,5 | 14,5 | 15 | 15 | 15,5 | 16 | 16 | 17 | 17,5 | 18 |
18 | 18,5 | 18,5 | 19,5 | 19,5 | 20,5 | 21 | 21,5 | 22 | 23 |
23,5 | 24 | 25 | 25,5 | 28 | 29 | 30 | 30,5 | 32 | 34,5 |
Далі будуємо статистичні розподіли частот і відносних частот:
варіанта | -9 | -6 | -3,5 | -0,5 | 0,5 | 2 | 3 | 4,5 | 5,5 | 7 |
частота | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
відносна | 0.02 | 0.02 | 0.02 | 0.02 | 0.02 | 0.02 | 0.02 | 0.02 | 0.02 | 0.02 |
|
|
|
|
|
|
|
|
|
|
|
варіанта | 8 | 9,5 | 10 | 11 | 11,5 | 12 | 12,5 | 13 | 13,5 | 14,5 |
частота | 1 | 1 | 1 | 1 | 2 | 1 | 1 | 2 | 1 | 1 |
відносна | 0.02 | 0.02 | 0.02 | 0.02 | 0.04 | 0.02 | 0.02 | 0.04 | 0.02 | 0.02 |
|
|
|
|
|
|
|
|
|
|
|
варіанта | 15 | 15,5 | 16 | 17 | 17,5 | 18 | 18,5 | 19,5 | 20,5 | 21 |
частота | 2 | 1 | 2 | 1 | 1 | 2 | 2 | 2 | 1 | 1 |
відносна | 0.04 | 0.02 | 0.04 | 0.02 | 0.02 | 0.04 | 0.04 | 0.04 | 0.02 | 0.02 |
|
|
|
|
|
|
|
|
|
|
|
варіанта | 21,5 | 22 | 23 | 23,5 | 24 | 25 | 25,5 | 28 | 29 | 30 |
частота | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
відносна | 0.02 | 0.02 | 0.02 | 0.02 | 0.02 | 0.02 | 0.02 | 0.02 | 0.02 | 0.02 |
|
|
|
|
|
|
|
|
|
|
|
варіанта | 30,5 | 32 | 34,5 |
| ||||||
частота | 1 | 1 | 1 | |||||||
відносна | 0.02 | 0.02 | 0.02 | |||||||
б) Полігон частот і полігон відносних частот - відкладемо на осі абсцис варіанти xi, а на осі ординат – відповідні їм частоти ni (відносні частоти vi).
З'єднавши точки (xi;ni) відрізками прямих, одержимо невідомий полігон частот.
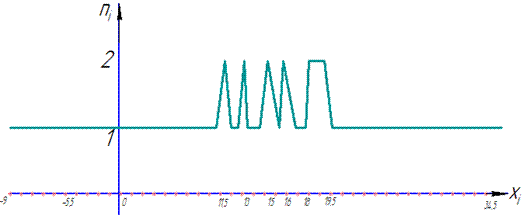
Полігон відносних частот буде аналогічним, треба замінити 1на 0,02, а 2 на 0,04.
в) Розбивши вибірку на 5 рівних інтервалів (по 10 елементів), виконуємо побудову гістограми частот:

Гістограму відносних частот будувати легко, оскільки кожен елемент вибірки на досліджуваних інтервалах зустрічається лише один раз.

г) Емпіричну функцію розподілу знаходимо за формулою Fn(x)=nx/n, де nx кількість елементів вибірки, що менші за x.
Беремо значення із таблиці та знаючи, що обсяг вибірки n=50, записуємо емпіричну функцію розподілу:
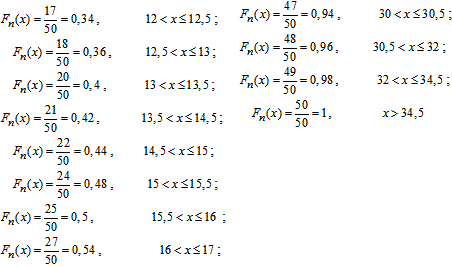
Графік емпіричної функції розподілу має вигляд:
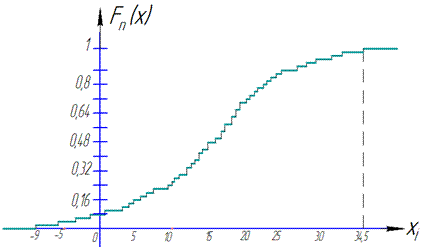
Її побудова займає найбільше часу, тому якщо є можливість, краще використовувати MathCad, Maple чи інші математичні пакети.
Самий оптимальний варіант - завантажити з інтернету програму для аналізу статистичних розподілів.
Їх зараз багато, в тому числі і під андроїди.
Приклад 3 Результати досліджень характеризуються наступними вибірками.
Необхідно побудувати:
а) ранжований варіаційний ряд, статистичні розподіли частот і відносних частот;
б) полігон частот і полігон відносних частот;
в) гістограму частот і гістограму відносних частот, розбивши вибірку на 5 рівних інтервалів;
г) записати емпіричну функцію розподілу і побудувати її графік.
варіанта | 100 | 101 | 102 | 103 | 104 | 105 | 106 | 107 | 108 |
частота | 2 | 3 | 8 | 12 | 8 | 7 | 5 | 3 | 2 |
відносна | 0,04 | 0,06 | 0,16 | 0,24 | 0,16 | 0,14 | 0,1 | 0,06 | 0,04 |
Розв'язання: а) Ранжований варіаційний ряд за зростанням:
30 | 30 | 31 | 31 | 31 | 32 | 32 | 32 | 32 | 32 |
32 | 32 | 32 | 33 | 33 | 33 | 33 | 33 | 33 | 33 |
33 | 33 | 33 | 33 | 33 | 34 | 34 | 34 | 34 | 34 |
34 | 34 | 34 | 35 | 35 | 35 | 35 | 35 | 35 | 35 |
36 | 36 | 36 | 36 | 36 | 37 | 37 | 37 | 38 | 38 |
Статистичні розподіли частот і відносних частот:
варіанта | 30 | 31 | 32 | 33 | 34 | 35 | 36 | 37 | 38 |
частота | 2 | 3 | 8 | 12 | 8 | 7 | 5 | 3 | 2 |
відносна | 0.04 | 0.06 | 0.16 | 0.24 | 0.16 | 0.14 | 0.10 | 0.06 | 0.04 |
б)Полігон частот і полігон відносних частот. Відкладемо на осі абсцис варіанти xi, а на осі ординат – відповідні їм частоти ni(відносні частоти wi).
З'єднавши точки (xi;ni) відрізками прямих, одержимо шуканий полігон частот (відносних частот):
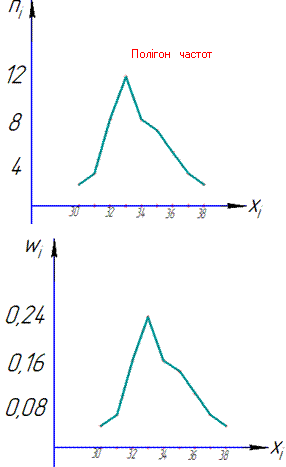
в) Гістограма частот (вибірка розбита на 5 рівних інтервалів):
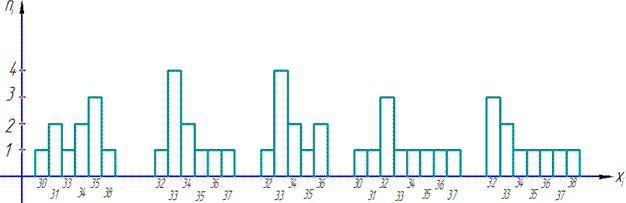
Гістограма відносних частот (в кожному інтервалі по 10 елементів):
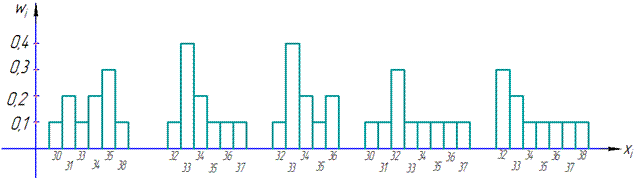
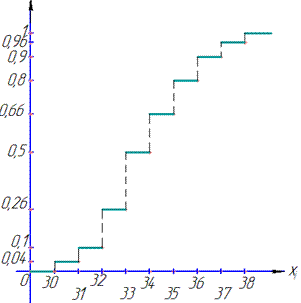
г) Емпіричну функцію розподілу визначатимемо за формулою Fn(x)=nx/n де nx – кількість елементів вибірки, що менші за x.
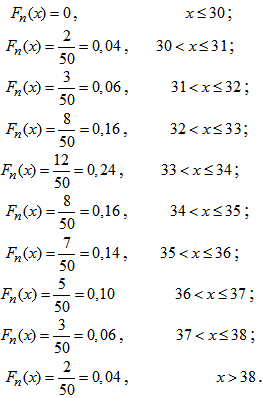
Використовуючи таблицю і враховуючи, що обсяг вибірки n=50, запишемо емпіричну функцію розподілу: Графік емпіричної функції розподілу має вигляд:
Приклад 4 Результати досліджень характеризуються наступними вибірками.
Необхідно побудувати:
а) ранжований варіаційний ряд, статистичні розподіли частот і відносних частот;
б) полігон частот і полігон відносних частот;
в) гістограму частот і гістограму відносних частот, розбивши вибірку на 5 рівних інтервалів;
г) записати емпіричну функцію розподілу і побудувати її графік.
26 | -9,1 | 9,5 | 18 | 17,5 | 11 | 5,5 | -12 | 7 | 12 |
19,5 | 24,5 | 28,5 | 2 | 8,5 | 10 | 13,5 | 15,5 | -4 | 23 |
12,5 | -6,5 | 9 | 17 | -1,5 | 7,5 | 14,5 | -15 | 24 | 11,5 |
19 | -0,5 | 5 | 12,5 | 4 | 5,5 | -5,5 | 22 | 10 | -3 |
6,5 | 7 | 3,5 | 1 | 12 | 9 | 16 | 6 | 13,5 | 15 |
Розв'язання: а) Ранжований варіаційний ряд за зростанням:
-15 | -12 | -9,1 | -6,5 | -5,5 | -4 | -3 | -1,5 | -0,5 | 1 |
2 | 3,5 | 4 | 5 | 5,5 | 5,5 | 6 | 6,5 | 7 | 7 |
7,5 | 8,5 | 9 | 9 | 9,5 | 10 | 10 | 11 | 11,5 | 12 |
12 | 12,5 | 12,5 | 13,5 | 13,5 | 14,5 | 15 | 15,5 | 16 | 17 |
17,5 | 18 | 19 | 19,5 | 22 | 23 | 24 | 24,5 | 26 | 28,5 |
Статистичні розподіли частот і відносних частот:
варіанта | -15 | -12 | -9,1 | -6,5 | -5,5 | -4 | -3 | -1,5 | -0,5 | 1 |
частота | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
відносна | 0.02 | 0.02 | 0.02 | 0.02 | 0.02 | 0.02 | 0.02 | 0.02 | 0.02 | 0.02 |
|
|
|
|
|
|
|
|
|
|
|
варіанта | 2 | 3,5 | 4 | 5 | 5,5 | 6 | 6,5 | 7 | 7,5 | 8,5 |
частота | 1 | 1 | 1 | 1 | 2 | 1 | 1 | 2 | 1 | 1 |
відносна | 0.02 | 0.02 | 0.02 | 0.02 | 0.04 | 0.02 | 0.02 | 0.04 | 0.02 | 0.02 |
|
|
|
|
|
|
|
|
|
|
|
варіанта | 9 | 9,5 | 10 | 11 | 11,5 | 12 | 12,5 | 13,5 | 14,5 | 15 |
частота | 2 | 1 | 2 | 1 | 1 | 2 | 2 | 2 | 1 | 1 |
відносна | 0.04 | 0.02 | 0.04 | 0.02 | 0.02 | 0.04 | 0.04 | 0.04 | 0.02 | 0.02 |
|
|
|
|
|
|
|
|
|
|
|
варіанта | 15,5 | 16 | 17 | 17,5 | 18 | 19 | 19,5 | 22 | 23 | 24 |
частота | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
відносна | 0.02 | 0.02 | 0.02 | 0.02 | 0.02 | 0.02 | 0.02 | 0.02 | 0.02 | 0.02 |
|
|
|
|
|
|
|
|
|
|
|
варіанта | 24,5 | 26 | 28,5 |
| ||||||
частота | 1 | 1 | 1 | |||||||
відносна | 0.02 | 0.02 | 0.02 | |||||||
б)Полігон частот і полігон відносних частот. Відкладемо на осі абсцис варіанти xi, а на осі ординат – відповідні їм частоти ni(відносні частоти wi).
З'єднавши точки (xi;ni) відрізками прямих, одержимо шуканий полігон частот (відносних частот):
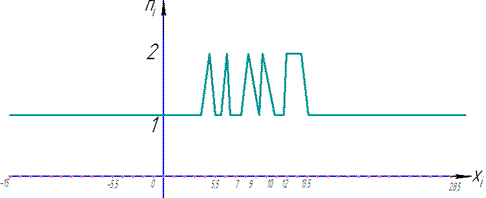
Полігон відносних частот буде аналогічним, треба замінити 1на 0,02, а 2 на 0,04.
в) Гістограма частот (вибірка розбита на 5 рівних інтервалів):

Гістограма відносних частот (в кожному інтервалі по 10 елементів):

г) Емпіричну функцію розподілу визначатимемо за формулою Fn(x)=nx/n де nx – кількість елементів вибірки, що менші за x.

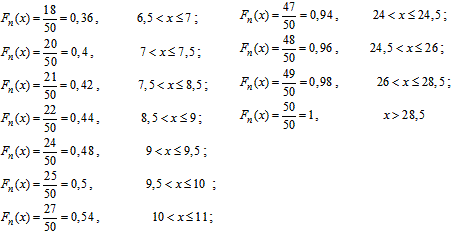
Використовуючи таблицю і враховуючи, що обсяг вибірки n=50, запишемо емпіричну функцію розподілу:
Графік емпіричної функції розподілу має вигляд:
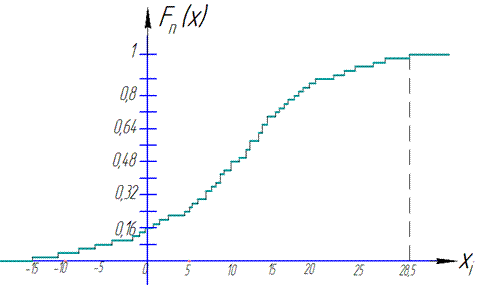
Приклад 5 Результати досліджень характеризуються наступними вибірками.
- Необхідно побудувати:
- а) ранжований варіаційний ряд, статистичні розподіли частот і відносних частот;
- б) полігон частот і полігон відносних частот;
- в) гістограму частот і гістограму відносних частот, розбивши вибірку на 5 рівних інтервалів;
- г) записати емпіричну функцію розподілу і побудувати її графік.
12 | -5,5 | 10 | 18 | -0,5 | 8,5 | 15,5 | -14 | 25 | 12,5 |
20 | 0,5 | 6 | 13,5 | 5 | 6,5 | -4,5 | 23 | 11 | -2 |
7,5 | 8 | 4,5 | 2 | 13 | 10 | 17 | 7 | 14,5 | 16 |
6,5 | -11 | 8 | 13 | 20,5 | 25,5 | 29,5 | 3 | 9,5 | 11 |
14,5 | 16,5 | -3 | 24 | 13,5 | 27 | -8,1 | 10,5 | 19 | 18,5 |
Розв'язання: а) Ранжований варіаційний ряд за зростанням:
-14 | -11 | -8,1 | -5,5 | -4,5 | -3 | -2 | -0,5 | 0,5 | 2 |
3 | 4,5 | 5 | 6 | 6,5 | 6,5 | 7 | 7,5 | 8 | 8 |
8,5 | 9,5 | 10 | 10 | 10,5 | 11 | 11 | 12 | 12,5 | 13 |
13 | 13,5 | 13,5 | 14,5 | 14,5 | 15,5 | 16 | 16,5 | 17 | 18 |
18,5 | 19 | 20 | 20,5 | 23 | 24 | 25 | 25,5 | 27 | 29,5 |
Статистичні розподіли частот і відносних частот: варіанта
варіанта | -14 | -11 | -8,1 | -5,5 | -4,5 | -3 | -2 | -0,5 | 2 | 4,5 |
частота | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 2 | 1 | 1 |
відносна | 0.02 | 0.02 | 0.02 | 0.02 | 0.02 | 0.02 | 0.02 | 0.04 | 0.02 | 0.02 |
|
|
|
|
|
|
|
|
|
|
|
варіанта | 5 | 6 | 6,5 | 7 | 7,5 | 8 | 8,5 | 9,5 | 10 | 10,5 |
частота | 1 | 1 | 2 | 1 | 1 | 2 | 1 | 1 | 2 | 1 |
відносна | 0.02 | 0.02 | 0.04 | 0.02 | 0.02 | 0.04 | 0.02 | 0.02 | 0.04 | 0.02 |
|
|
|
|
|
|
|
|
|
|
|
варіанта | 11 | 12 | 12,5 | 13 | 13,5 | 14,5 | 15,5 | 16 | 16,5 | 17 |
частота | 2 | 1 | 1 | 2 | 2 | 2 | 1 | 1 | 1 | 1 |
відносна | 0.04 | 0.02 | 0.02 | 0.04 | 0.04 | 0.04 | 0.02 | 0.02 | 0.02 | 0.02 |
|
|
|
|
|
|
|
|
|
|
|
варіанта | 18 | 18,5 | 19 | 20 | 20,5 | 23 | 24 | 25 | 25,5 | 27 |
частота | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
відносна | 0.02 | 0.02 | 0.02 | 0.02 | 0.02 | 0.02 | 0.02 | 0.02 | 0.02 | 0.02 |
|
|
|
|
|
|
|
|
|
|
|
варіанта | 29,5 |
| ||||||||
частота | 1 | |||||||||
відносна | 0.02 | |||||||||
б) Полігон частот і полігон відносних частот. Відкладемо на осі абсцис варіанти xi, а на осі ординат – відповідні їм частоти ni (відносні частоти wi).
З'єднавши точки (xi;ni) відрізками прямих, одержимо шуканий полігон частот (відносних частот):
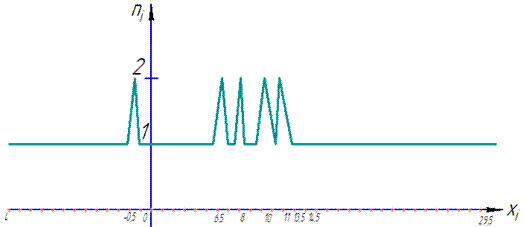
Полігон відносних частот буде аналогічним, треба замінити 1на 0,02, а 2 на 0,04.
в) Гістограма частот (вибірку розбили на 5 рівних інтервалів):

Гістограма відносних частот (в кожному інтервалі по 10 елементів, тому wi=0.01):

г) Емпіричну функцію розподілу визначатимемо за формулою Fn(x)=nx/n де nx – кількість елементів вибірки, що менші за x (їх тут аж 42, тому саму функцію не наводимо, через її громідскість), n=50.
Графік емпіричної функції розподілу має вигляд:
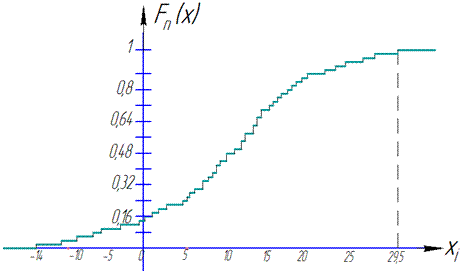
Використовуйте наведений алгоритм розрахунків, він легкий для запам'ятовування і вимагає знання найпростіших інтегралів.
Збережіть сторінку в закладки, якщо інформація допомогла Вам в навчанні. Якщо виникають труднощі в розрахунках чи побудові гістограм звертайтесь за допомогою.
Попереду Вас ще чекає чимало готових відповідей з теорії ймовірностей!


