Відповіді до контрольної роботи допоможуть підтягнути з практичних самого лінивого студента. Аналізуйте розв'язки контрольної з теорії ймовірностей та обчислюйте задачі за наведеними схемами.
Контрольна робота №1. ВАРІАНТ – 16
Завдання 1 Навмання складається букет із трьох квіток. Серед квіток є 6 айстр, 5 троянд та 3 ромашки.
Знайти ймовірність того, що букет складається:
- а) із трьох троянд;
- б) із трьох ромашок;
- в) із 1 троянди, 1 ромашки та 1 айстри.
Розв'язання: Схема обчислень такого сорту задач з ймовірності полягає в знаходженні числа всіх можливих подій, далі числа сприятливих подій. Сама ймовірність рівна відношенню цих чисел p=m/n.
При такому формулюванні обчислення проводимо через формулу розміщень
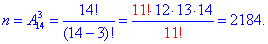
Уважно перегляньте, як спростовувати факторіали в дробі.
а) Число сприятливих подій рівна кількость способів, за якими можна вибрати 3 троянди із 5 можливих (розміщення з 5 по 3):
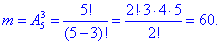
Ймовірність скласти букет із трьох троянд рівна:
P(A)=m/n=60/2184=0,0275.
б) Число способів, за якими можна вибрати 3 ромашки із 3 можливих рівне m=3*2*1=6.
Ймовірність склаcти букет з трьох ромашок рівна частці чисел:
P(B)=6/2184=0,00275.
в) Число сприятливих подій, за якими можна вибрати 1 троянду з 5, 1 ромашку з 3 і 1 айстру з 6 рівне добутку відповідних розміщень:
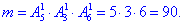
Ймовірність події C, при якій складають букет із 1 троянди, 1 ромашки та 1 айстри рівна:
P(C)=m/n=90/2184=0,0412.
Дану задачу можна розв'язати другим способом.
а) Маємо 14 квіток, потрібно вибрати 3 троянди з 5. Першу можна вибрати з ймовірністю p1=5/14, після того залишиться 4 троянди і 13 квіток. Тоді другою троянду можна витягнути з ймовірністю p2=4/13, і 3 троянду в букеті з ймовірністю p3=3/12. Ймовірнысть скласти букет із трьох троянд рівна добутку ймовірностей
p=p1*p2*p3=5/14*4/13*3/12= 5/182=0,0275.
Методика не складна і її під силу вивчити за кілька прикладів.
б) Для цього пункту важливо, що маємо 3 ромашки з 14 квітів, а букет має містити всі 3 ромашки. Не розписуючи всі міркування, знайдемо ймовірність за попередньою схемою
p=p1*p2*p3=3/14*2/13*1/12= 1/364=0,00275.
в) Ймовірність буде рівна добутку часток квітів, при цьому слід враховувати, що їх кількість буде зменшуватися на одиницю при кожному виборі
p=p1*p2*p3=5/14*3/13*6/12= 15/364=0,0412.
При цьому порядок вибору квітів (перша троянда чи третя) не змінює ймовірність скласти з них букет.
Завдання 2 Студент знає 20 питань із 25 програми. Знайти ймовірність, що студент із трьох запитань відповів:
- а) на одне запитання;
- б) на всі запитання;
- в) не відповів на жодне.
Розв'язання: Число можливих способів, за якими можна вибрати 3 запитання із 25, тобто кількість різних білетів знаходимо за формулою розміщень:
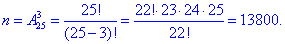
а) Число способів, за якими студент відповів на одне запитання з 3 рівне добутку розміщень:
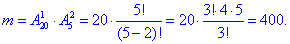
Перше з них означає, що вибираємо 1 питання з 20 на які студент знає відповідь, друге- кількість варіантів вибрати 2 питання з 5.
Ймовірність події A, при якій студент відповів на одне запитання з 3 рівна частці:
P(A)=m/n=400/13800=0,029.
б) Число способів, за якими можна вибрати білет із 3 запитанням, на які він знає відповідь рівна розміщенню з 20 по 3:
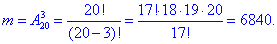
Ймовірність такої події B знаходимо за класичною формулою:
P(B)=m/n=6840/13800=0,4957.
в) Останнє значення ймовірності приймає найменше з усіх значень. А все тому, що студент вивчив більшість питань на екзамен, і лише є 60 способів витягнути 3 питання з 5 , на які він не знає відповіді:
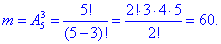
Ймовірність події C, при якій студент не відповів на жодне запитання рівна:
P(B)=m/n=60/13800=0,0043.
Ось і всі пояснення до задачі.
Завдання 3 На контроль надійшли вироби, які виготовлені трьома робітниками. Перший виготовив 20 виробів, серед яких 4% браку, другий – 30 виробів, в яких 1% браку, а третій – 50, серед яких 5% браку. Взята навмання деталь виявилась бракованою.
Знайти ймовірність того, що виріб виготовив 3-й робітник.
Розв'язання: Задачу обчислюємо за формулою повної ймовірності та Байєса. За першою знаходимо ймовірність витягнути браковану деталь, за Байєсом - ймовірність виготовлення бракованої деталі 3 робітником.
Позначимо через Hi - гіпотези, що виріб виготовлений і-м робітником (i=1,2,3).
Тоді ймовірність кожної з гіпотез рівна частці виробів в загальній сукупності:
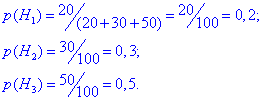
Сума ймовірностей повинна бути рівна одиниці. Якщо у Вас в сумі не виходить одиниця, значить Ви вже "накосячили", шукайте помилку.
Нехай подія A полягає в тому, що взята навмання деталь бракована. Тоді на основі умови можемо виписати ймовірності того, що браковану деталь виготовив кожен робітник:
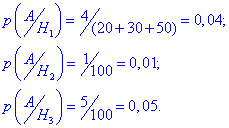
За формулою повної ймовірності знаходимо ймовірність, що деталь бракована: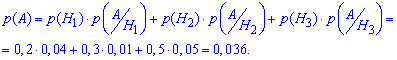 
Ймовірність що браковану деталь виготовив 3-й робітник знаходимо за формулою Байєса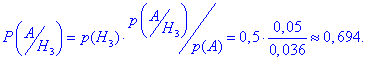
Вона рівна частці третього доданку в попередньо знайденій ймовірності.
Завдання 4 Ймовірність попадання в мішень при одному пострілі 0,6. Знайти ймовірність того, що при 250 пострілах в мішень попали:
- а) 100 разів;
- б) не менше 150 і не більше 200.
Розв'язання: а) Завдання на вигляд просте, однак багато з Вас розгубиться, якщо таку задачу розмістити серед простеньких. Для седе запам'ятайте, що при великій кількості випробувань + треба знайти ймовірність попадання в проміжок - це вже підказка застосовувати локальну та інтегральну теорему Лапласа. Якщо, наприклад, мені потрібно знайти точну відповідь на питання б) то в Maple чи іншому мат. пакеті я можу 50 раз застосувати формулу Бернуллі, яка дає найточніше значення, а далі все просумувати.
Проблема в тому, що при теперішньому рівні компютеризації Вас всіх вчат по таблицях шукати наближені значення функцій Лапласа, замість вчити обчислювати їх та всі формули, що є в теорії ймовірностей в математичних пакетах.
Оскільки ймовірність не залежить від історії (попередніх пострілів), то за формулою Бернуллі знаходимо точне значення
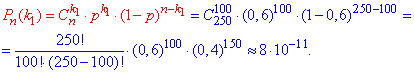Однак його ми точно знайшли не калькулятором, оскільки при піднесенні до 100 і 150 степеня похибка була б великою.
Вам же потрібно швидко оцінити ймовірність, тому наближене її значення знаходимо за локальною теоремою Лапласа.
Оскільки умова застосування формули Лапласа n*p*q=250*0,6*0,4=60>10 виконується, то відхилення від точного значення має бути мінімальним
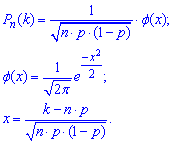
Виконаємо обчислення x:
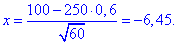
За таблицями табулювання локальної функції Лапласа маємо phi
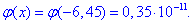
і саме значення ймовірності
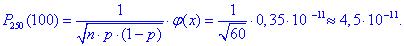Порівнюючи показники степеня при основі (-11) робимо висновок, що розбіжність з формулою Бернуллі невелика!
б) Ймовірність, що не менше 150 і не більше 200 попали в мішень при 250 пострілах знайдемо за інтегральною формулою Лапласа:
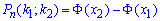
де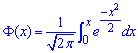 
- інтегральна функція Лапласа;
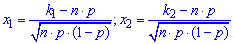- аргументи інтегральної функції розподілу.
Знайдемо точки x1=0, x2=6,45
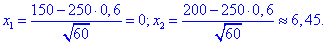
та виконуємо кінцеві обчислення
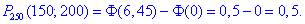
Щоб розв'язати задачу з теорії ймовірностей в Maple достатньо наступного коду
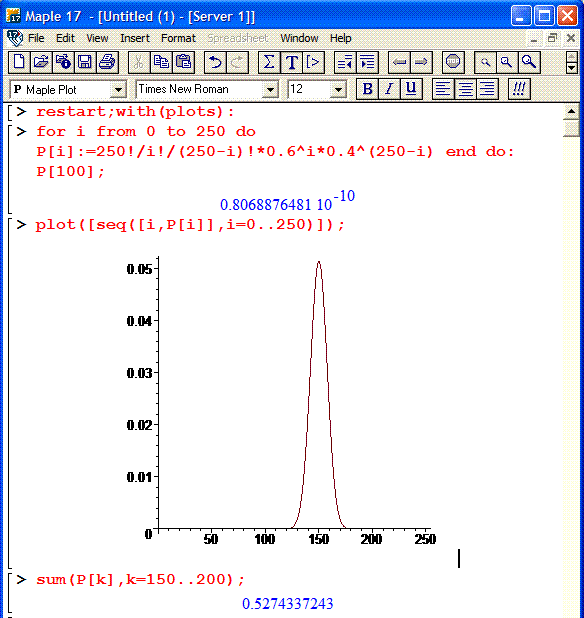
в результаті отримаємо всі потрібні значення + графік розподілу ймовірнотей
> restart;with(plots):
> for i from 0 to 250 do P[i]:=250!/i!/(250-i)!*0.6^i*0.4^(250-i) end do:
> P[100];
0.8068876481*10-10
> plot([seq([i,P[i]],i=0..250)]);
> sum(P[k],k=150..200);
0.5274337243
Щоб переконати Вас, що все насправді так легко наведу Вам фрагмент розрахунків
Завдання 5 В партії 10% нестандартних деталей. Взято чотири (n=4). X - число нестандартних серед відібраних. Знайти закон розподілу випадкової величини X, знайти математичне сподівання випадкової величини M(X), дисперсію D(X), середньоквадратичне відхилення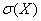 
, функцію розподілу F(X) та побудувати її графік.
Розв'язання: Оскільки від досліду до досліду ймовірність не змінюється (а саме p=0,1 і q=1-p=0,9), то відбирання нестандартних деталей змінюється за самим поширеним серед інших біноміальним законом:
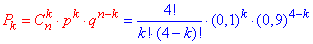
Результати для 4 деталей запишемо у таблицю:
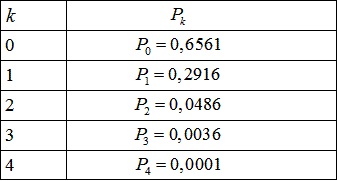Графік закону розподілу має вигляд
Математичне сподівання випадкової величини M(X)=n*p=4*0,1=0,4.
Дисперсія D(X)=n*p*q= 4*0,1*0,9=0,36.
Середнє квадратичне відхилення випадкової величини X:
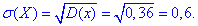
Функцію розподілу випадкової величини X знайдемо за формулою:
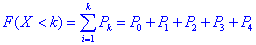
Результати запишемо в таблицю:
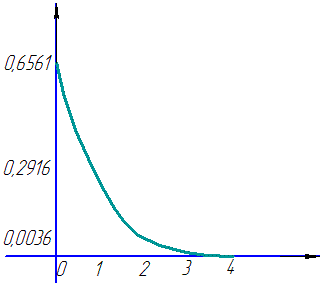
Графік функції розподілу має вигляд
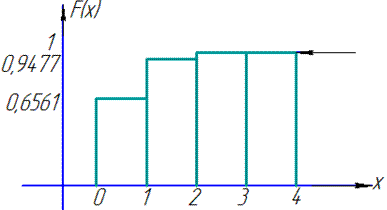На цьому задача розв'язана.
Завдання 6 Випадкова величина задана щільністю розподілу f(x):
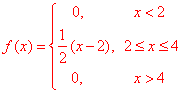
Знайти функцію розподілу F(X), математичне сподівання випадкової величини M(X), дисперсію D(X) випадкової величини та ймовірність того, що в результаті випробувань x набуде значень, що належать інтервалу (a;b). Побудувати графіки f(x) та F(x).
Розв'язання: Функцію розподілу знаходимо через інтеграл від щільності:
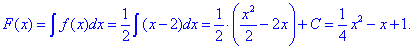
Сталу інтегрування знаходимо з умови, що функція розподілу на кінці рівна одиниці F(4)=1.
Пам'ятайте про те, що вона повинна приймати значення выд 0 до одииці і бути неперервною.
Звідси 4-4+С=1, С=1.
Графік щільності f(x) та функції розподілу F(x) навдено нижче:
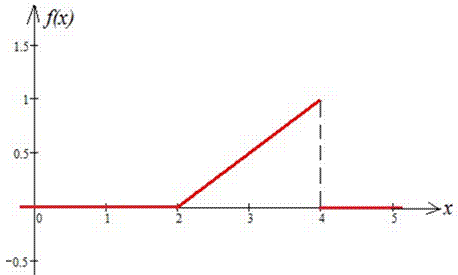
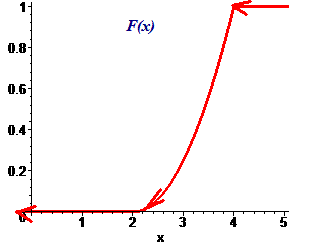Математичне сподівання знахидомо інтегруванням:
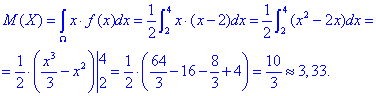
Дисперсію через інтеграл обчислюємо за формулою:
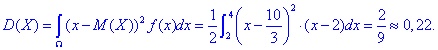
Ймовірність того, що в результаті випробувань x набуде значень, що належать інтервалу (a;b) рівна інтегралу:
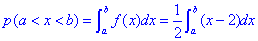
Його значення обчисліть самостійно.
Завдання 7 Відомі математичне сподівання a=12 та середнє квадратичне відхилення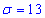 
випадкової величини x, яка розподілена нормально.
Обчислити ймовірність того, що
- а) ця випадкова величина прийме значення, які належать інтервалу
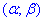=(10;20); - б) абсолютна величина відхилення |x-a|<6 буде менше за
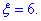
Розв'язання: а) Для знаходження імовірності того, що випадкова величина x прийме значення, які належать інтервалу 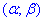скористаємось інтегральною формулою Лапласа :
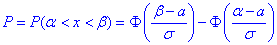
На краях інтервалу отримаємо такі значення
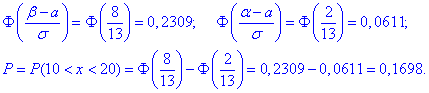
Просумувати їх не складає великих проблем.
б) Для знаходження імовірності того, що абсолютна величина відхилення |x-a|<6 буде менше за 6 скористаємось формулою:
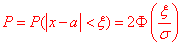
З таблиці знаходимо значення
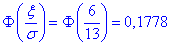
та множимо його на 2
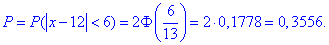
Це і буде ймовірність, що абсолютна величина відхилення менша за 6.
На цьому розбір контрольної завершено, більше готових відповідей на типові задачі з теорії ймовірностей шукайте на сторінках сайту.
