Перевірку чи вектори перпендикулярні або колінеарні виконують при проходженні теми "Вектори".
Умова перпендикулярності

Якщо вектори перпендикулярні, то їх скалярний добуток a•b=0 рівний нулю:
ax•bx+ay•by+az•bz=0.
Інша умова, що також вимагає обчислення скалярного добутку полягає в тому, що косинус кута між перпендикулярними векторами рівний нулю
cos(phi)=0.
Розглянемо завдання на ознаку перпендикулярності.
Приклад 1. Чи перпендикулярні вектори?
1. a(-2;3;0), b(6;4;-11);
2. c(-8;5), d(1;7).
Розв'язання:Обчислюємо скалярний добуток векторів a,b:
a•b=-2•6+3•4+0•(-11)=0.
Вектори перпендикулярні a⊥b, оскільки їх скалярний добуток рівний нулю.
Перевіримо другу пару векторів, обчислимо скалярний добуток
c•d=-8•1+5•7=27.
Робимо висновок, що вектори c,d не перпендикулярні, оскільки ознака перпендикулярності не виконується
c•d=27≠0.
Далі розглянемо тести із ЗНО підготовки, де потрібно перевірити умову перпендикулярності.
Приклад 42.11 При якому значенні x вектори a(2;x) і b(-4;10) перпендикулярні?
А | Б | В | Г | Д |
-5 | -0,8 | 0,8 | 5 | 20 |
Розв'язування: Вектори a(2;x) і b(-4;10) будуть перпендикулярними (a⊥b), якщо їх скалярний добуток дорівнюватиме нулю:
a•b=0.
З умови перпендикулярності a•b=2•(-4)+x•10=0 обчислюємо параметр x:
-8+10x=0,
10x=8,
x=8:10=0,8.
В декартовій площині вони мають вигляд
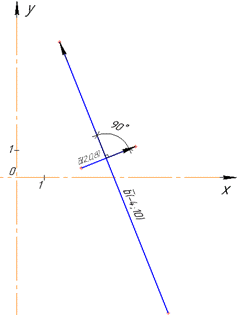
Відповідь: 0,8 – В.
Приклад 42.27 Установити відповідність між значеннями числа x (1–4), та парами векторів (А–Д), які за цих значень взаємно перпендикулярні.
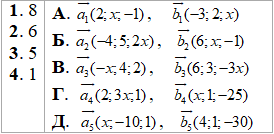
Розв'язування: Умова перпендикулярності векторів an(a1;a2;a3) і bn(b1;b2;b3):
a⊥b, якщо a1b1+a2b2+a3b3=0.
Для кожної пари векторів обчислюємо скалярний добуток векторів і прирівнюємо його до нуля. Отримане рівняння розв'язуємо відносно "ікс"
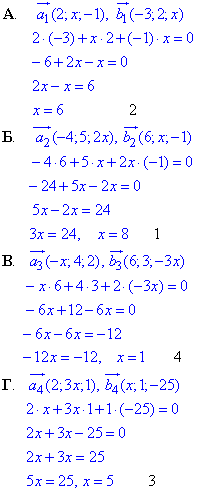
Записуємо відповідь до тестів:
1 – Б, 2 – А, 3 – Г, 4 – В.
На ЗНО тестах такі завдання поширені, тому запам'ятайте алгоритм обчислень.
Приклад 42.20 a і b – ненульові вектори. |a+b|=|a-b|. Знайти кут між векторами a і b.
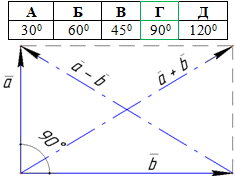
Розв'язування: В умові рисунку немає, його виконано на основі всіх розрахунків.
Нехай φ – кут між векторами a і b, виписуємо модуль суми та різниці векторів.
Далі прирівнявши довжини, складаємо рівняння для знаходження кута між векторами
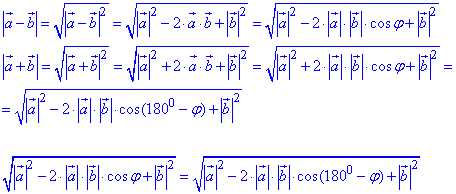
Підносимо до квадрату та спрощуємо подібні доданки
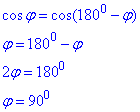
Робимо висновок, що якщо |a+b|=|a-b|, то кут між векторами a і b дорівнює 90 градусів.
З рисунка добре видно, що при побудові суми (a+b) і різниці (a-b) векторів за правилом паралелограма отримали прямокутник, у якого (за властивістю) діагоналі є рівними (|a+b|=|a-b|).
Відповідь: 900 – Г.
Приклад 42.37 Знайти площу паралелограма, побудованого на векторах AB(3;0;-4) і AD(0;5;0).
Розв'язування: Знайдемо скалярний добуток векторів AB(3;0;-4) і AD(0;5;0):
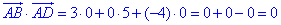
він рівний нулю.
Це означає, що вектори перпендикулярні AB⊥AD і паралелограм ABCD є прямокутником.
Знайдемо модуль (довжину) вектора AB(3;0;-4):
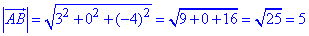
Знайдемо модуль (довжину) вектора AD(0;5;0):
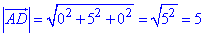
Оскільки у прямокутника дві сусідні сторони рівні, то він є квадратом. Знайдемо площу заданого паралелограма (квадрата) ABCD:
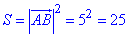
Відповідь: 25.
Скалярний добуток обчислюють через досить просту формулу, тому великого різноманіття прикладів на умову перпендикулярності Ви не знайдете. Спробуйте обчислити кілька завдань самостійно, Ви побачите, що тема не важка для вивчення. Набагато важчими в плані розрахунків є завдання на обчислення довжини суми чи різниці векторів, обчислення площ чи об'ємів тіл побудованих на векторах, але це вже інша тема.


