Дослідження збіжності рядів є важливим з точки зору їх оцінки та необхідним у випадку обчислення суми ряду. Ознак збіжності рядів декілька, популярна і достатньо проста в застосуванні для рядів з додатними членами - ознака збіжності Даламбера. Нижче буде розібрано ряд прикладів на встановлення збіжності ряду за ознакою Далабера, спробуйте для себе взяти максимум потрібного.
Приклад 1. Дослідити числовий ряд на збіжність.
а)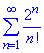 
Досліджувати збіжність ряду будемо за ознакою Даламбера:
якщо границя відношення наступного члена прогресії до заданого менша одиниці і додатна 0<α<1 при номері прямуючому до безмежності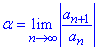 
, тоді ряд 
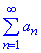збігається, і розбігається, якщо α>1 .
Виконаємо обчислення
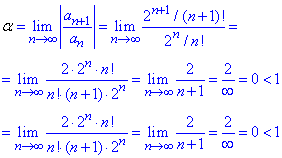
звідси слідує, що ряд 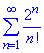збігається.
б)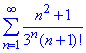 
Дослідимо збіжність ряду за ознакою Даламбера:
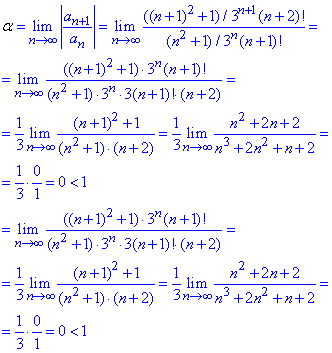
звідси слідує, що ряд 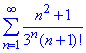збігається.
Приклад: 2.5 Дослідити збіжність рядів
а)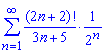 
Обчислення: Оскільки даний ряд має додатні члени, то досліджувати його на збіжність будемо за допомогою ознаки Даламбера:
Записуємо загальний член ряду та наступний, що йде після нього
Та знаходимо границю їх частки
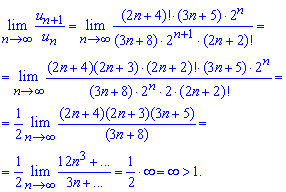
Оскільки границя нескінченна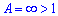 
, то за ознакою Деламбера ряд розбіжний.
б)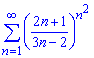 
Обчислення: Члени ряду додатні, тому досліджувати на збіжність будемо за ознакою Даламбера: Записуємо формули послідовних членів ряду
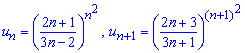
Та знаходимо границю наступного члена до попереднього при n прямуючому до безмежності
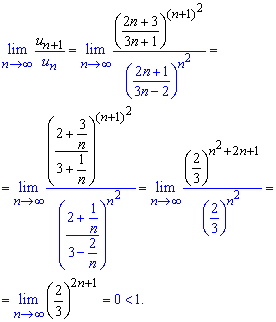
Границя рівна нулю, так як показник прямує до нескінченності, а в дужках маємо значення менше за одиницю.
За теоремою Даламбера A=0<1 ряд збігається!
Приклад: 2.8 Дослідити ряди на збіжність:
а)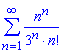 
Обчислення: Як Ви вже переконалися усі приклади, що тут розглядаються слід перевіряти за ознакою Даламбера.
В результаті спрощення прийдемо до другої чудової границі – експоненти
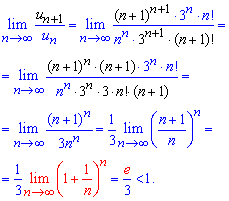
Загалом границя менша одиниці 
отже ряд збігається.
б)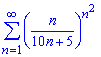 
Обчислення: Для перевірки на збіжність ряду за ознакою Даламбера обчислюємо границю
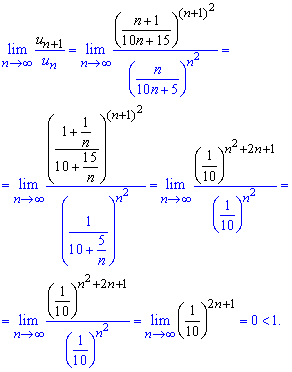
Границя рівна 0 (A=0<1), отже ряд збігається!
Приклад: 2.14 Дослідити ряд на збіжність
а)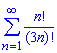 
Обчислення: Знаходимо границю частки наступного члена ряду до попереднього
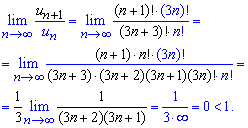
Для зручності читання формул наступний член ряду виділений під границею чорним кольором. Добре розберіться як ділити факторіал на факторіал.
За ознакою Даламбера ряд збігається!
б)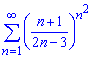 
Обчислення: Записуємо формулу загального члена ряду та наступного за ним
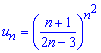
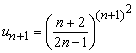
Підставляємо їх в формулу Даламбера та обчислюємо границю
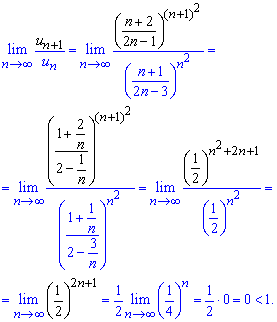
Границя рівна нулю 0<1, а це значить що даний ряд збігається.
Приклад: 2.16 Дослідити ряд на збіжність:
а)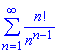 
Обчислення: За ознакою Даламбера перевіряємо границю членів ряду на обмеженість
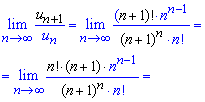
Перетворивши множники в чисельнику і знаменнику дробу зведемо функцію в дужках до другої чудової границі
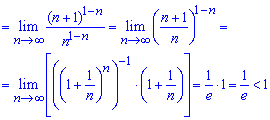
Оскільки границя менша одиниці
,
то за теоремою Даламбера ряд збігається.
б)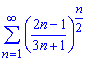 
Обчислення: Задано числовий степеневий ряд з додатніми членами. Знайдемо границю відношення наступного члена ряду до попереднього
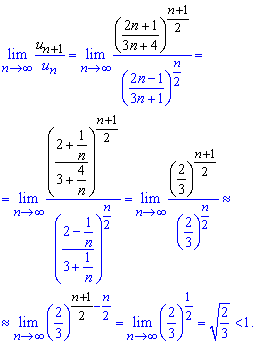
При обчисленні границі думаю всі моменти Вам зрозумілі, якщо ні то Вам потрібно переглнути категорію "границі функцій".
Отримали гранию менше одиниці,
отже за ознакою Даламбера ряд збіжний.
Приклад: 2.26 Дослідити збіжність ряду:
а)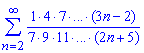 
Обчислення: Для застосування ознаки Даламбера випишемо загальний член ряду та наступний за ним
Далі підставимо їх та знайдемо границю
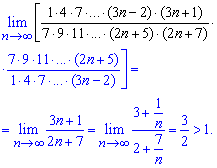
Границя рівна A=3/2>1, а це означає що даний ряд розбігається!
б)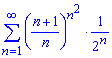 
Обчислення: Записуємо два послідовні члени додатного ряду
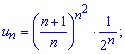
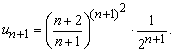
Знаходимо границю для оцінки збіжності ряду за теоремою Даламбера.
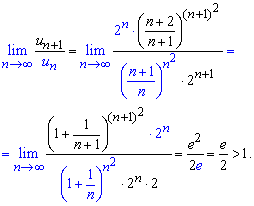
В ході обчислень отримаємо другу чудову границю (експоненту) як в чисельнику, так і в знаменнику. Результуюча границя більша одиниці 
, отже робимо висновок про розбіжність ряду.
Готові розв'язки на ряди:
