Теорема 1 (радикальна ознака Коші): Якщо для ряду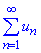 
з додатними членами un>0 існує границя
Тоді: при A<1 ряд збігається;
при A>1 ряд розбігається;
при A=1 питання про збіжність ряду ознака не вирішує.
Це маєте запам'ятати, оскільки на значення границі Коші базуються висновки про збіжність або розбіжність числового ряду.
А тепер перейдемо то аналізу готових відповідей з розрахункових та екзаменаційних робіт.
Приклад 1. Дослідити на збіжність ряд
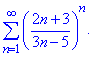
Розв'язування: Маємо додатний ряд, причому він має вигляд функції від n в степені функції від n. Це важливо, тому що тільки в такому випадку радикальна ознака Коші швидко встановлює збіжність або розбіжність ряду.
Знаходимо границю за формулою
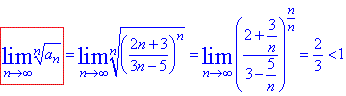
Границя менша одиниці (lim=2/3<1), тому за ознакою Коші ряд збігається.
Приклад 2. Дослідити на збіжність ряд
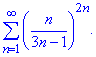
Розв'язування: Ряд знакододатний і необхідна умова збіжності виконується.
Знаходимо границю за ознакою Коші
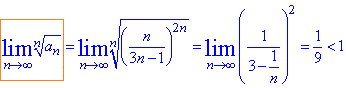
Вона менша одиниці, тому робимо висновок про збіжність ряду.
Приклад 3. Дослідити на збіжність ряд
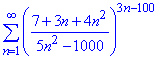
Розв'язування: Задані додатні члени ряду, які спадають з ростом номера.
Візьмемо границю кореня n-го степеня від загального члена при номері прямуючому до безмежності
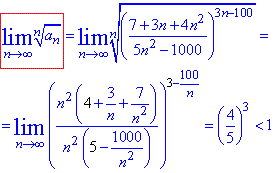
Limit=64/125<1, отже за радикальною ознакою Коші ряд збігається.
Приклад 4. Дослідити на збіжність ряд
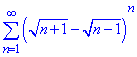
Розв'язування: Маємо різницю коренів в степені n, тому для доведення збіжності застосуємо ознаку Коші. Для розкриття границі домножуємо різницю коренів на їх суму, щоб позбутися невизначеності.
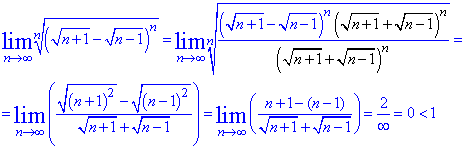
Границя рівна нулю, тому ряд збігається за ознакою Коші.
На багатьох уроках сайту знайомимо Вас з тим, як виконувати аналогічні обчислення в математичних пакетах.
В Мейплі досить вдало реалізовано обчислення границь.
Для прикладу, щоб знайти задану достатньо скомпілювати наступний код:
restart;
limit(sqrt(n+1)-sqrt(n-1), n = infinity)
В результаті отримаємо знайдену границю
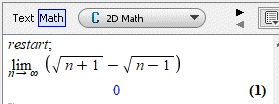
Приклад 5. Дослідити на збіжність ряд
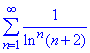
Розв'язування: Маємо ряд у вигляді дробу де в знаменнику степенева залежність від ln(n+2). Границю за радикальною ознакою Коші знайти легко.
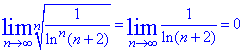
За ознакою Коші ряд збіжний.
Приклад 6. Довести, що ряд збіжний
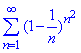
Розв'язування: Для знаходження границі зведемо загальний член ряду під другу особливу границю.
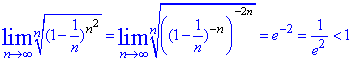
Границя менша одиниці, тому ряд за Коші збігається.
Знайдемо цю ж границю в Мейплі:
lim(((1-1/n)^(n^2))^(1/n), n = infinity);
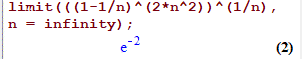
Для подальшої роботи Вам зажди стануть в нагоді знання мат. пакетів, особливо коли роботи пов'язані з обчисленнями та візуалізацією даних.
Приклад 7. Довести збіжність ряду
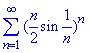
Розв'язування: Оскільки вивчаємо радикальну ознаку Коші, то зрозуміло, що її тут будемо використовувати.
Але спершу скористаємося ознакою порівняння. Для цього Ви повинні знати еквівалентні нескінченно малі величини.
Для заданого ряду
sin(1/n)≈1/n при n→∞.
Підставляємо в границю
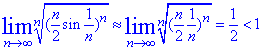
Границя =1/2<1, тому ряд збіжний.
Код для обчислення границі в Мейпл:
limit((n/2)*sin(1/n), n = infinity);
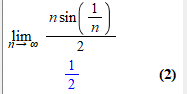
Сам хід розрахунків зашитий в ядрі програми, зате результат точно перевіряти не потрібно, оскільки розробники гарантують достовірність результатів.
Приклад 8. Дослідити на збіжність ряд
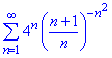
Розв'язування: При застосуванні радикальної ознаки Коші розпишемо вираз в дужках під правило другої визначної границі.
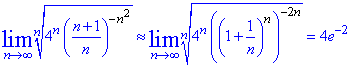
За ознакою Коші даний ряд збігається, оскільки
lim = 4/e^2≈0,55.
Приклад 9. Довести, що ряд розбігається
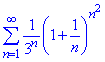
Знаходимо границю за формулою
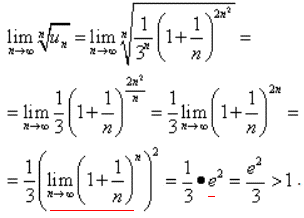
При розкритті границі використано формулу другої важливої границі.
lim=e^2/3≈2,718^2/3=2,46>1, тому за радикальною ознакою Коші ряд розбігається.
Приклад 10. Дослідити, що ряд збігається
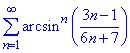
Знаходимо границю кореня n-го порядку від un=arcsinn((3n-1)/(6n+7)):
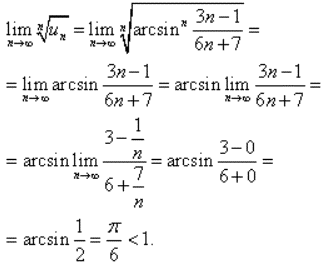
Границя π/6≈0,52(3)<1 менша одиниці, тому за ознакою Коші ряд збіжний.
З уроки Ви взнали багато нового вивчили, побачили, що без знання границь Вам непросто буде досліджувати збіжність рядів. В математиці багато тем перетинаються, і чим більше Ви будете вміти, тим легше будуть даватися для вивчення нові теми.
