Відповіді до контрольної роботи з диференціальних рівнянь (ДР) не так і легко знайти в інтернеті. Часто вони містять легкі завдання лише на однорідні ДР або неоднорідні першого порядку з яких Ви точно не зможете охопити весь матеріал і навчитися вирішувати диференціальні рівняння вищих порядків, складати характеристичні рівняння, знати в якому вигляді шукати розв'язки неоднорідного рівняння. Ми постаралися цю проблеми вирішити і зібрали в одному місці всі можливі типи ДР, які Вас можуть чекати на контрольній роботі, тестах, індивідуальних завданнях чи модулі. З кожного прикладу є посилання на відповіді до тематично подібних диференціальних рівнянь. Зразу можу відмітити, що завдання не з легких, хоча алгоритм їх вирішення відповідає всім рівням складності.
Студенти Львівського національного університету ім. І. Франка серед відповідей до ДР можуть знайти варіанти, які їх чекатимуть на контрольній. ВУЗи Києва, Одеси, Харкова та інших міст України мають подібну програму з ДР, тому теж знайдуть масу готових прикладів. В загальному теорія з диференціальних рівнянь повністю сформована, тому алгоритмами обчислень незмінні і ними може користуватися кожен, хто вирішив вивчати диференціальні рівняння.
Приклад 1. (1.25) Знайти загальний інтеграл диференціального рівняння
Розв'язання: Маємо диференціальне рівняння першого порядку розписане через диференціали. Схема обчислення рівнянь такого типу полягає у розділенні змінних, в результаті цієї операції отримаємо диференціальне рівняння з відокремленими змінними, розв'язок якого знаходимо інтегруванням. Отже спершу групуємо доданки, що містять dx, dy та переносимо по різні сторони знаку "="
Після цього всі множники, що містить y при dx переносимо до dy, те ж саме проробляємо з множниками , що містять змінну x при dy. У такий спосіб зведемо початкове рівняння до диференціального рівняння з відокремленими змінними
Далі зінтегруємо отриману залежність.
Щоб швидко це зробити чисельники вносимо під диференціал
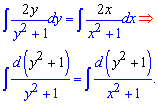
Така маніпуляція дозволяє за допомогою табличного інтегралу отримати логарифми
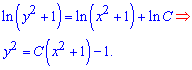
Сталу теж вносимо під логарифм, щоб вкінці прийти до компактного запису загального інтегралу диференціального рівняння. Цю формулу не вартує більше розписувати, оскільки можна не врахувати корені. Більшість би з Вас записала, що функція рівна додатному кореню з правої частини, проте це не правильно. Від'ємний корінь також є розв'язком заданого рівняння, тому якщо записувати, то наступним чином
Проте такий запис важче читати і при формуванні відповіді радимо зупинятися на попередньому кроці.
Більше праці – не завжди означає кращий результат.
Приклад 2. (2.26) Знайти загальний інтеграл диференціального рівняння
Розв'яязання: Маємо однорідне диференційне рівняння 0 порядку. В цьому легко переконатися, якщо в праву сторону замість x,y підставити t*x,t*y
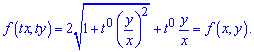
З аналізу правої сторони бачимо, що можемо застосувати підстановку z=y/x, звідси y=z*x.
Не забуваючи, що нова змінна залежить від аргументу виражаємо похідну "y" за правилом добутку
та з врахуванням заміни переписуємо початкове ДР у вигляді
Змінну z переносимо в праву сторону
та розділяючи змінні, переходимо до диференціального рівняння з відокремленими змінними
Інтегруємо залежність
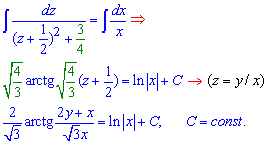
Остання формула і є загальним інтегралом диференціального рівняння. Такий запис ще називають рівнянням не розв'язаним відносно у(х). Виділити у даному випадку у(х) можливо, проте отримаємо менш змістовну формулу ніж кінцева.
Приклад 3. (3.5) Знайти загальний інтеграл рівняння:
Розв'язання: Задано ДР першого порядку , яке звідне до однорідного диференціального рівняння. Щоб отримати останнє знайдемо стаціонарну точку, для цього розв'яжемо систему рівнянь, яку формуємо прирівнюючи чисельник та знаменник до нуля
Далі виконуємо зміщення початку координат в знайдену точку O(1;1)
,
Початкове ДР при такій заміні зводимо до вигляду
Після цього у правій частині змінну X виносимо з чисельника та знаменника за дужки та скорочуємо на неї. В такий спосіб отримаємо однорідне диференціальне рівняння нульового порядку
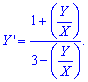
Далі використовуємо схему обчислень з попереднього завдання. Робимо заміну: z=Y/X; Y=z*X, похідна старої функції при цьому виражається формулою
Підставимо у рівняння та спростимо його
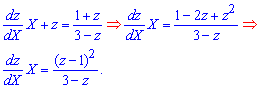
Далі перетворюємо до диференціального рівняння з відокремленими змінними
та інтегруванням обчислюємо його
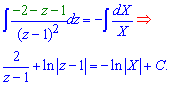
Вертаючись двічі до попередніх замін, отримаємо
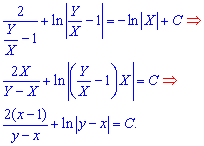
Остання формула і є шуканий загальний інтеграл диференціального рівняння. Вона неявно зв'язує функцію y(x) та аргумент.
Приклад 4. (4.6) Знайти розв'язок задачі Коші:
Розв'язання: Задано неоднорідне диференціальне рівняння першого порядку. Запишемо та проінтегруємо відповідне однорідне рівняння (ліва частина):
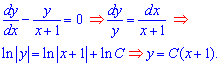
Схема обчислень тут використана стандартна – розділили змінні та про інтегрували. Далі, щоб задовільнити неоднорідну частину рівняння покладаємо, що стала є функцією аргумента C=C(x). Запишемо функцію та її похідну
Далі підставимо у ДР та після інтегрування знайдемо вигляд сталої C=C(x)
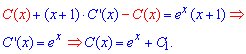
Записуємо загальний розв'язок неоднорідного диференціального рівняння в кінцевому вигляді
Ров'яжемо задачу Коші. Сталу C1 довизначимо з умови
.
Звідси отримаємо
- частковий розв'язок рівняння.
Приклад 5. (5.7) Знайти розв'язок задачі Коші для рівняння Бернуллі
Розв'язання: Перед Вами новий тип неоднорідних диференціальних рівняння першого порядку. Розділити змінні в цьому випадку є неможливо. Для обчислень такого роду ДР використовуємо схему Бернуллі, робимо заміну змінних y=u*v, y'=u'v+uv', де в добутку фігурують функції u=u(x) і v=v(x) від аргумента. В нових позначеннях ДР приймає вигляд
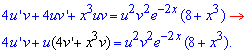
Далі рівняння слід розділити на 2, з яких по черзі визначити функції. Спершу дужку в лівій частині (виділена чорним) прирівняємо до нуля
Таке ДР для Вас не складне і подібних Ви розв'язували чимало. Записуємо рівняння в диференціалах, далі зводимо до ДР з відокремленими змінними та інтегруючи його знаходимо одну із функцій
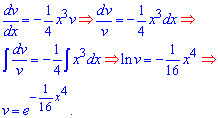
Отримали експоненту з від'ємним показником квадрату аргументу. При підстановці v у початкове ДР отримаємо
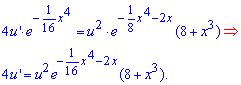
Знову розділяємо змінні та інтегруємо, тільки вкінці тут потрібно додати константу.
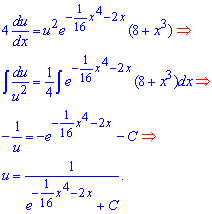
Дві функції ми визначили, можемо записати загальний розв'язок диференціального рівняння.
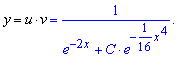
Але це ще не кінець розрахунків. Знайдемо частковий розв'язок диференціального рівняння (задача Коші), для цього пригадаємо початкову умову з якої до визначаємо сталу
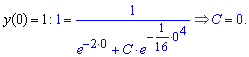
При підстановці С=0 в формулу отримаємо компактний частковий розв'язок диференціального рівняння y=e2x.
Приклад 6. (6.21) Знайти загальний інтеграл диференціального рівняння:
Розв'язання: Ліва частина ДР може бути повним диференціалом функції двох змінних u(x,y).
Щоб перевірити це знайдемо часткові похідні, зокрема для множника при dx похідну беремо по dy, для іншого по dx. Умова повного диференціалу має вигляд
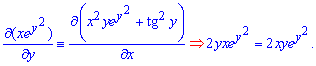
Вона справджується, отже можемо відновити функцію інтегруванням
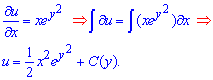
Якщо інтегруємо по аргументу то стала залежна від функції і навпаки. Це важливо, оскільки потрібно, щоб функція задовольняла дві часткові похідні. А для цього диференціюємо знайдену функцію по "ігрик" та прирівнюємо з множником ДР при dy
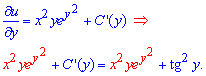
Отримаємо рівняння на похідну від сталої з якого інтегруванням знаходимо C(y)
Загальний інтеграл диференціального рівняння при цьому рівний
Приклад 7. Знайти частинний розв'язок диференціального рівняння другого порядку.
x^2y''=(y')^2, y(1)=1/2, y'(1)=1.
Обчислення: Зробимо заміну: y'=p, де p=p(x), тоді y''=p'.
В такий спосіб понизимо степінь ДР, яке обчислюємо методом розділення змінних
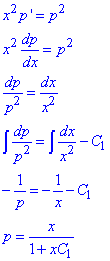
Повернемося до заміни y'=p:
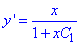
Підставимо початкову умову y'(1)=1 і знайдемо сталу C1:
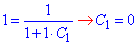
Отримали просте ДР y'=x, розписуємо та інтегруємо:
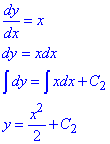
Підставимо початкову умову y(1)=1/2 і знайдемо C2:
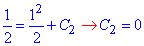
Підставляємо,
y=x^2/2 - частинний розв'язок заданого диференціального рівняння.
Приклад 8. Знайти загальний розв'язок диференціального рівняння другого порядку.
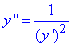
Обчислення: Виконуємо заміну:
y'=p, де p=p(y), тоді y"=p"p. Отож,
Перетворимо ДР
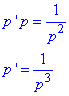
Отримали диференціальне рівняння першого порядку, яке зводиться до рівнянь з відокремлюваними змінними.
Розв'яжемо отримане рівняння:
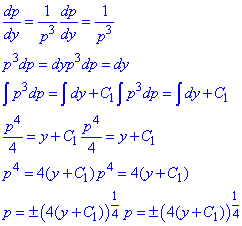
Повернемося до заміни:
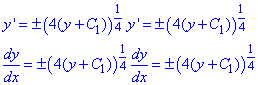
Отримали диференціальне рівняння першого порядку з відокремлюваними змінними.
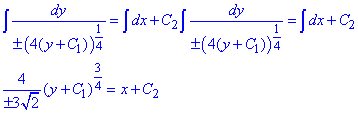
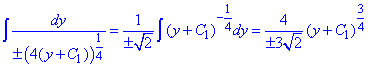– загальний розв'язок заданого диференціального рівняння.(*)
На цьому перша частина контрольної роботи розглянута, далі будуть рівняння в повних диференціалах, що потребують визначення інтегруючого множника та неоднорідні диференціальні рівняння 2, 3 порядку.
