Готові відповіді до прикладів на однорідні диференціальні рівняння шукає чимало студентів, далі Ви їх зможете детально розібрати. Але перш ніж перейти до розгляду прикладів рекомендуємо уважно прочитати короткий теоретичний матеріал.
Рівняння виду P(x,y)dx+Q(x,y)dy=0, де функції P(x,y) і Q(x,y) є однорідними функціями одного порядку називають однорідним диференціальним рівнянням (ОДР).
Схема розв'язання однорідного диференціального рівняння
1. Спершу потрібно застосувати підстановку y=z*x, де z=z(x) – нова невідома функція (в такий спосіб вихідне рівняння зводиться до диференціального рівняння з відокремлюваними змінними (ДРВЗ).
2.Похідна добутку y'=(z*x)'=z'*x+z*x'=z'*x+z або в диференціалах dy=d(zx)=zdx+xdz.
3.Підставляємо нову функцію у та її похідну y'(або dy) в ДР з відокремлюваними змінними відносно x та z.
4.Розвязавши диференціальне рівняння з відокремлюваними змінними, зробимо обернену заміну y=z*x, тому z= y/х, і отримаємо загальний розв'язок (загальний інтеграл) диференціального рівняння.
5.Якщо задано початкову умову y(x0)=y0, то знаходимо частинний розв'язок задачі Коші. В теорії все звучить легко, протее на практиці не у всіх так весело виходить рішати диф. рівняння. Тому для поглиблення знань розглянемо поширені приклади. На легких завданнях немає особливо, що Вас навчити, тому зразу перейдемо до складніших.
Обчислення однорідних диференціальних рівнянь
Приклад 1. (2.8) Знайти загальний інтеграл диференціального рівняння
Розв'язання: Ділимо праву сторону рівняння на змінну, яка стоїть множником біля похідної. В результаті прийдемо до однорідного диференційного рівняння 0 порядку
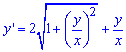
І тут багатьом мабуть стало цікаво, як визначити порядок однорідного рівняння? Питання достатньо доречне, а відповідь на нього наступна: в праву сторону підставляють замість функції та аргумента значення t*x, t*y. При спрощенні отримують параметр "t" в певному степені k, його і називають порядком рівняння. В нашому випадку "t" скоротиться, що рівносильно 0-му степені або 0-му порядку однорідного рівняння.
Далі в правій стороні можемо перейти до нової змінної y=zx; z=y/x .
При цьому не забуваємо виразити похідну "y" через похідну нової змінної. За правилом частки знаходимо
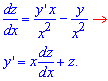
Рівняння в диференціалах набуде вигляду
Спільні доданки в правій і лівій частині скорочуємо та переходимо до диференціального рівняння з відокремленими змінними.
Інтегруємо обидві частини рівняння
Для зручності подальших перетворень постійну зразу вносимо під логарифм
За властивостями логарифмів отримане рівняння еквівалентне наступному
На цьому рівняння ще не розв'язане, необхідно повернутися до виконаної заміни змінних
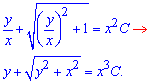
Це і є загальний розв'язок диференційного рівняння. Якщо Ви уважно читали попередні уроки, то ми наголошували, що схему обчислення рівнянь з відокремленими змінними ви повинні вміти застосовувати вільно і такі рівняння доведеться обчислювати для складніших типів ДР.
Приклад 2. (2.14) Знайти загальний інтеграл диференціального рівняння
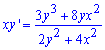
Розв'язання: Схема обчислень однорідних та звідних до них ДР Вам знайома. Переносимо змінну в праву сторону рівняння, а також в чисельнику та знаменнику виносимо x2, як спільний множник
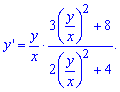
В такий спосіб отримаємо однорідне ДР нульового порядку.
Наступним кроком вводимо заміну змінних z=y/x, y=z*x, про яку постійно будемо нагадувати, щоб Ви її завчили
Після цього ДР зводимо до вигляду
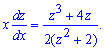
Далі перетворимо залежність до диференціального рівняння з відокремленими змінними
та інтегруванням розв'язуємо його.
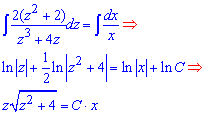
Інтеграли не складні, решта перетворень виконано на основі властивостей логарифма. Остання дія включає експонування логарифма. Вкінці повертаємося до початкової заміни та записуємо розв'язок диференціального рівняння
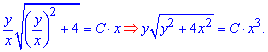
Константа "C" приймає будь-яке значення. Всі хто навчається заочно мають проблеми на екзаменах з даним типом рівнянь, тому просьба уважно переглянути та запам'ятати схему обчислень.
Приклад 2*. Знайти загальний розв'язок однорідного диференціального рівняння першого порядку.
xy'-y'=(x+y)ln((x+y)/x).
Обчислення: Розділимо обидві частини рівняння на "ікс"
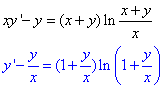
зробимо заміну y=z•x, тобто z=y/x.
Підставимо в ДР, розділимо змінні та розв'яжемо шляхом інтегрування:
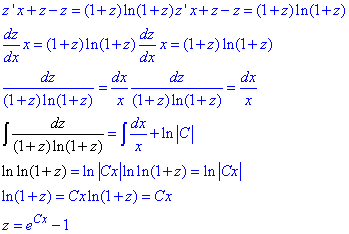
Повернемося до початкових змінних "z=y/x":
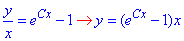- загальний розв'язок рівняння.
При інтегруванні лівої частини рівняння використали заміну змінних
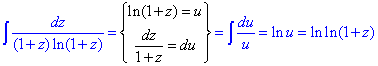
Приклад 3. (2.16) Знайти загальний інтеграл диференціального рівняння
Розв'язання:Як слідує з наведеної вище методики, диференціальні рівняння такого типу розв'язують методом введення нової змінної. Перепишемо залежність так, щоб похідна була без змінної
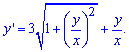
Далі з аналізу правої частини бачимо, що всюди присутня частка, її і позначаємо за нову невідому z=y/x, y=z*x.
Знаходимо похідну від y
З врахуванням заміни початкове ДР перепишемо у вигляді
Однакові доданки спрощуємо, а все що отримали зводимо до ДР з відокремленими змінними
Інтегруванням обох частин рівності
приходимо до розв'язку у вигляді логарифмів
Експонуючи залежності загальний розв'язок рівняння зводимо до запису
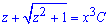
який після підстановки у нього початкової заміни змінних набуде вигляду
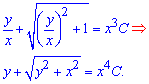
Тут С – стала, яку можна довизначити з умови Коші. Якщо не задана задача Коші то стала приймає довільне дійсне значення.
Ось і вся мудрість в обчисленні однорідних диференціаьних рівнянь.
