Наступний тип рівнянь називають звідними до однорідних ДР. Для студентів вони достатньо болючі, оскільки важко ідентифікувати такого роду ДР з першого погляду. Інша проблема - не всі можуть вивчити та знати, коли і яку схему слід застосовувати.
Проте схема обчислень достатньо добре описана в підручниах та дає можливість знайти розв'язок ДР, хоч при цьому приходиться виконувати масу обчислень. Щоб не лякати Вас зразу перейдемо до аналізу готових відповідей з яких все стане зрозумілим.
Приклад 1 (3.11) Знайти загальний інтеграл диференціального рівняння
![]() Розв'язання: Перед нами зовсім інший тип диф. рівнянь ніж ті, що були розглянуті раніше. Схема обчислень теж відрізняється, спершу необхідно визначити стаціонарну точку - для цього маємо знайти нулі чисельника і знаменника.
Розв'язання: Перед нами зовсім інший тип диф. рівнянь ніж ті, що були розглянуті раніше. Схема обчислень теж відрізняється, спершу необхідно визначити стаціонарну точку - для цього маємо знайти нулі чисельника і знаменника.
Розв'яжемо систему рівнянь:
![]()
Стаціонарною точкою є М(-1;1).
Далі виконуємо заміну змінних (зміщення координат)
![]()
звідси вихідне ДР перетворимо до однорідного диференціального рівняння
![]() або
або ![]()
Виконаємо заміну змінних 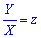 , та знаходимо диференціал через нову змінну
, та знаходимо диференціал через нову змінну
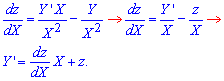
Підставляючи в рівняння, отримаємо просту для обчислень залежність
![]()
яку легко зводимо до рівняння з відокремленими змінними
![]()
Далі інтегруємо обидві частини
![]()
та знаходимо загальний розв'язок рівняння
![]()
Вертаючись до самої першої заміни, отримаємо
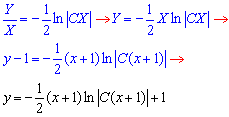
де 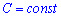 - довільна константа.
- довільна константа.
Ось в такому вигляді отримали загальний інтеграл диференціального рівняння. Добре розберіть наведену схему обчислень, вона для студентів на ціну золота.
Приклад 2 (3.17) Знайти загальний інтеграл диференціального рівняння
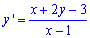 Розв'язання: Дане диференціальне рівняння має розв'язок, проте не кожен студент без шпаргалки чи методички може знайти відповідь самостійно.
Розв'язання: Дане диференціальне рівняння має розв'язок, проте не кожен студент без шпаргалки чи методички може знайти відповідь самостійно.
Методика зведення рівняння до однорідного полягає в наступних діях: знаходимо стаціонарну точку (нулі чисельника та знаменника дробу).
Для цього розв'язуємо систему лінійних рівнянь:
![]()
Далі вводимо заміну змінних
![]()
Одиниці справа є розв'язками системи рівнянь.
Наше початкове диф. рівняння в нових змінних матиме запис
![]()
Саме для цього і розв'язували систему рівнянь.
Далі необхідно виконати заміну:
![]() , тоді
, тоді ![]() .
.
Після заміни отримане ДР можемо звести до рівняння з відокремленими змінними
![]()
Інтегруванням обох частин
![]()
прийдемо спершу до логарифма
![]()
Експонуванням обох частин отримаємо залежність
![]()
Вертаючись до нашої заміни, отримаємо розв'язок в нових змінних
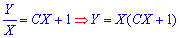
а далі остаточний інтеграл диференціального рівняння
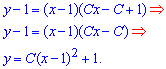
Де 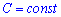 - довільна константа
- довільна константа
Ось так складно буває інколи отримати загальний розв'язок диференціального рівняння.
Приклад 3 (3.27) Розв'язати диференціальне рівняння
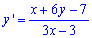 Розв'язання: Маємо ДР першого порядку, яке можна звести до однорідного диф. рівняння. Для цього знайдемо стаціонарну точку:
Розв'язання: Маємо ДР першого порядку, яке можна звести до однорідного диф. рівняння. Для цього знайдемо стаціонарну точку:
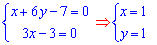
Маючи стаціонарну точку, виконуємо заміну координат
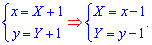 ,
,
Вихідне диференціальне рівняння перетвориться до вигляду
![]() або
або ![]()
Зробимо заміну змінних z=Y/X, Y=z*X, тоді похідна рівна
![]()
Підставимо її в рівняння та розділимо змінні, так отримаємо ДР з відокремленими змінними
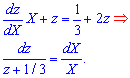
Інтегруємо диференціальне рівняння та приходимо до логарифмічного
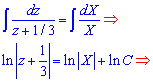
Експонуємо отриману залежність, попередньо звівши логарифми в правій частині за формулою добутку
![]() ,
,
Вертаючись до нашої заміни (z), отримаємо розв'язок
![]()
який після повторної заміни набуде зрозумілого вигляду
![]()
Перенісши одиницю вправо
![]()
отримаємо загальний розв'язок диференціального рівняння.
Тут розібрано лише 3 завдання, проте схему обчислень вони описують в повній мірі. Тепер Ви знаєте, що робити з рівняннями звідними до однорідних та після самостійної роботи з подібними прикладами не матимете труднощів на контрольних та екзаменах. Перегляньте наступні уроки, Вас чекає ще маса готових відповідей для вичення диференціальних рівнянь.


