Неоднорідні диференціальні рівяння (ДР) обчислюють за трошки довшою процедурою ніж однорідні, крім однорідного розв'язку необхідно встановити частковий розв'язок неоднорідного ДР. На практиці це відображається в розв'язуванні двох різних по схемі обчислень ДР. Якщо ще маємо умову Коші, то вкінці всіх пошуків розв'язку диференціального рівняння необхідно визначити значення сталих, що входить в функцію. Все це досить просто реалізується, тому переходимо до аналізу готових відповідей.
Приклад 1.(4.10) Знайти розв'язок задачі Коші для диференціального рівняння
Розв'язання: Маємо неоднорідне диференціальне рівняння першого порядку. Як поступати з такими рівняннями детально розглянуто на попередніх уроках.
Знайдемо спершу розв'язок однорідного ДР. Інтегруємо для цього рівняння (ліву частину), попередньо віокремивши змінні:
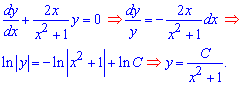
Далі вважаємо, що стала С(х) є функцією від змінної x
Все це робиться для того, щоб підібрати сталу таким чином, що диф. рівняння стане рівністю (щоб задовільнити неоднорідну функцію - права частина ДР).
Знайдемо похідну y' з врахуванням вище сказаного
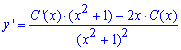
Підставляємо функцію та її похідну в початкове диференціальне рівняння
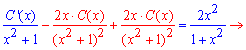
Бачимо, що два доданки при сумуванні дадуть нуль і в результаті отримаємо таку залежність для похідної сталої
З останнього рівняння методом інтегрування знаходимо явний вигляд сталої С(x)
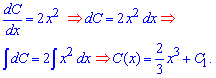
Після цього можемо записати загальний розв'язок рівняння
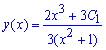
Але це ще не фінал обчислень, нам потрібно знайти частковий розв'язок (задача Коші). Для цього задовільняємо початкову умову та обчислюємо сталу
.
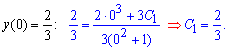Отже задача Коші розв'язана і знайдений частковий розв'язок диференціального рівняння можемо записати формулою
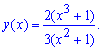
На цьому одне з рівнянь обчислено. Схема знаходження функції не надто запутана з однієї сторони, з іншої її легко реалізувати (сталу приймаємо за фунцію). Розглянемо ще кілька готових прикладів, а далі вчіться обчислювати самостійно.
Приклад 2. (4.16) Знайти розв'язок задачі Коші:
Розв'язання: Задано неоднорідне диференціальне рівняння першого порядку + умова Коші. Запишемо та проінтегруємо відповідне однорідне рівняння, попередньо звівши його до рівняння з відокремленими змінними:
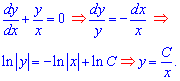
Розв'язок однорідного рівняння знайти в даному випадку досить легко. Вивчіть для практики внесення сталої в інтегралах під логарифм – це значно спростить подальші перетворення розв'язку. Далі розглянемо константу C(x) як функцію від змінної x:
Похідна y' за формулою похідної частки матиме вигляд
Підставимо функцію y та її похідну y' в початкове диференціальне рівняння та виразимо похідну сталої
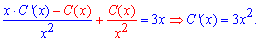
Інтегруванням знаходимо залежність C(x)
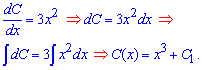
Замінивши сталу отриманим тільки що значенням, отримаємо загальний розв'язок диференціального рівняння
Розв'яжемо задачу Коші. З початової умови
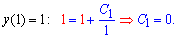
отримаємо y=x2 - частковий розв'язок диференціального рівняння.
Приклад 3. (4.18) Знайти розв'язок ДР та задачі Коші:
Розв'язання: Почнемо з аналізу лівої частини диференціального рівняння. Інтегруємо однорідне диференціальне рівняння, попередньо відокремивши у ньому змінні
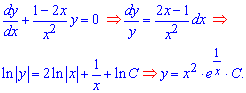
Для останнього переходу використали властивість експоненти - другий доданок записали як логарифм від експоненти ln(exp(1/x)). Тепер припустимо, що константа C(x) - це функція від змінної x:
тоді її похідна рівна
Підставляємо сталу і її похідну в вихідне диференціальне рівняння
яке після скорочення доданків перетвориться в залежність
З останнього рівняння знаходимо функцію C(x) інтегруванням
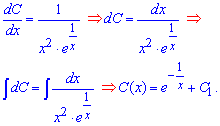
Отож, ми знайшли загальний розв'язок диференціального рівняння
Знайдемо частковий розв'язок рівняння (задача Коші). Задовільнимо початкову умову на функцію та обчислимо сталу
Звідси маємо y=x2 - частковий розв'язок рівняння. На вигляд простий запис, хоча на його обчислення потрачено чимало часу.
Часткові розв'язки двох останніх рівнянь співпадають, таке рідко буває на практиці. Тепер Ви знаєте, як розв'язати неоднорідне рівняння та задовіьнити умову Коші.
Якщо на екзамені чи контроьній Вам потрібна допомога - звертайтеся. Ми допомогли не одній тисячі студентів, зможемо допомогти і Вам.
